В этой лабораторной работе мы применим на практике математические формулы, которые мы видели на предыдущем уроке, чтобы увидеть, как MLE работает с нормальными распределениями.
Вы сможете:
Примечание. * Подробный вывод всех уравнений MLE с доказательствами можно увидеть на этом сайте. *
Давайте посмотрим пример MLE и фитингов распределения с Python ниже. Здесь scipy.stats.norm.fit вычисляет параметры распределения, используя оценку максимального правдоподобия.
from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np sample = Nonestats.norm.fit(data) чтобы подогнать распределение к приведенным выше данным. param = None
#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)x = np.linspace(-5,5,100) x = np . linspace ( - 5 , 5 , 100 )
# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None # Your code here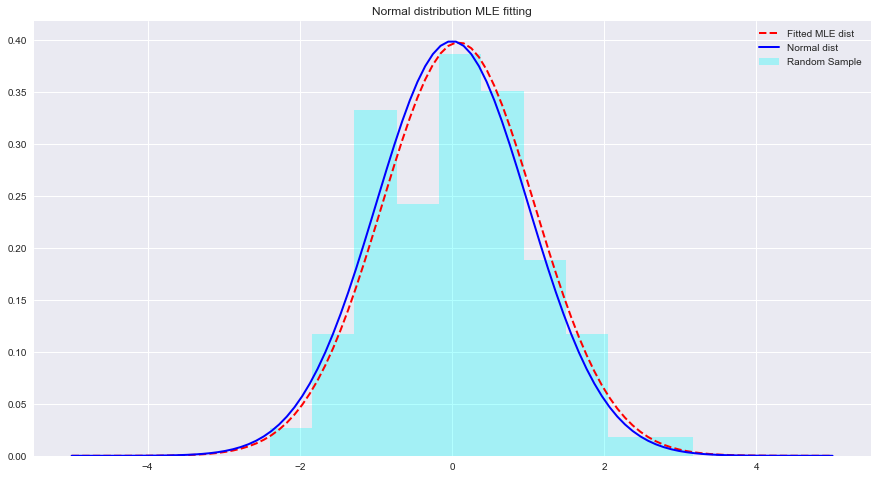 
# Your comments/observations В этой короткой лабораторной работе мы рассмотрели байесовский режим в гауссовском контексте, т.е. когда основные случайные величины имеют нормальное распределение. Мы узнали, что MLE может оценивать неизвестные параметры нормального распределения, максимизируя вероятность ожидаемого среднего значения. Ожидаемое среднее значение очень близко к среднему значению неподходящего нормального распределения в этом пространстве параметров. Мы продолжим понимать это и узнаем, как такие оценки выполняются при оценке средних значений ряда классов, присутствующих в распределении данных, с использованием наивного байесовского классификатора.
