การแยกย่อยอนุกรมเวลาหมายถึงการแยกออกเป็นองค์ประกอบต่างๆ ซึ่งโดยปกติจะเป็นองค์ประกอบแนวโน้มและองค์ประกอบที่ไม่ปกติ และหากเป็นอนุกรมเวลาตามฤดูกาล ก็จะถือเป็นองค์ประกอบตามฤดูกาล สำหรับข้อมูลหุ้น TSLA จากกราฟแนวโน้มราคา เราจะเห็นว่าข้อมูลไม่มีองค์ประกอบตามฤดูกาล แต่ข้อมูลอนุกรมเวลานี้ควรมีองค์ประกอบแนวโน้มและองค์ประกอบที่ไม่ปกติ การแยกย่อยอนุกรมเวลาเกี่ยวข้องกับการพยายามแยกอนุกรมเวลาออกเป็นองค์ประกอบเหล่านี้ กล่าวคือ การประมาณค่าองค์ประกอบแนวโน้มและองค์ประกอบที่ไม่ปกติ เราจะใช้ฟังก์ชัน SMA() เพื่อทำให้ข้อมูล TSLA ราบรื่น เราจะเลือกลำดับที่แตกต่างกัน (n=8 และ n=40) เพื่อตรวจสอบองค์ประกอบของแนวโน้ม เป้าหมายคือเราพยายามทำให้ข้อมูลราบรื่นด้วยค่าเฉลี่ยเคลื่อนที่แบบธรรมดา
รุ่นอาริม่า
ARIMA (Autoregressive Integrated Moving Average) เป็นเครื่องมือหลักที่ใช้ในการวิเคราะห์อนุกรมเวลาเพื่อพยายามคาดการณ์ค่าในอนาคตของตัวแปรตามมูลค่าปัจจุบัน สมการพยากรณ์ ARIMA(p,d,q) ตามทฤษฎีแล้ว แบบจำลอง ARIMA เป็นแบบจำลองประเภททั่วไปที่สุดสำหรับการพยากรณ์อนุกรมเวลา ซึ่งสามารถกำหนดให้เป็นแบบ "คงที่" ได้ด้วยการหาผลต่าง โมเดล ARIMA ถูกกำหนดไว้สำหรับอนุกรมเวลาที่อยู่กับที่ ดังนั้น หากคุณเริ่มต้นด้วยอนุกรมเวลาที่ไม่คงที่ คุณจะต้อง 'สร้างความแตกต่าง' อนุกรมเวลาก่อนจนกว่าคุณจะได้อนุกรมเวลาที่อยู่กับที่ หากต้องการแยกอนุกรมเวลา d เท่าเพื่อให้ได้อนุกรมคงที่ เราใช้ฟังก์ชัน diff() จากนั้น เราจะใช้การทดสอบ ADF อย่างเป็นทางการซึ่งไม่ปฏิเสธสมมติฐานว่างของการไม่อยู่กับที่ ซึ่งเป็นการยืนยันการตรวจสอบด้วยสายตาของเรา:
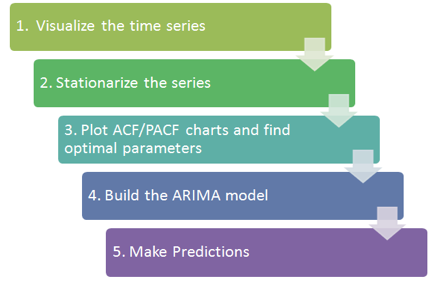
ในส่วนนี้ เราใช้ข้อมูลหุ้นของ TESLA เป็นอนุกรมเวลา เราแยกย่อยและใช้ HoltWinter exponential Smoothing และ ARIMA เพื่อคาดการณ์ราคาหุ้นในอนาคต ขั้นตอนพื้นฐานมีดังรูปต่อไปนี้
อีกประการหนึ่งคือเราควรวิเคราะห์ข้อผิดพลาดและปรับแต่งพารามิเตอร์โมเดลเพื่อให้ได้ผลลัพธ์ที่ดีขึ้นเสมอ