smard power forecasting
1.0.0
พื้นที่เก็บข้อมูลนี้มีไว้สำหรับคาดการณ์การใช้พลังงานของเยอรมนี
อิงและแรงบันดาลใจจาก:
แหล่งข้อมูล: SMARD
ใส่ไฟล์ที่ดาวน์โหลดทั้งหมดลงใน:
/example/dataset # there is already used dataset included if you pull, but you could update
ตรวจสอบไฟล์ Forecast.Rmd เพื่อดูว่าคุณสามารถเรียกใช้โค้ดนี้ในเวอร์ชันอัปเดตของ SMARD-Data ได้อย่างไร
ห้องสมุดที่ใช้:
# Probably needed
# Load Packages
# library(fhswf)
# library(tsibbledata)
# library(broom)
# library(readr)
# library(datasets)
# library(timeDate)
# library(qlcal)
# library(corrplot)
# library(mgcv)
# library(MEFM)
# library(TTR)
packages <- c(
"devtools",
"ggplot2",
"dplyr",
"tsibble",
"fable",
"fabletools",
"feasts",
"distributional",
"lubridate",
"tidyr",
"forecast",
"zoo",
"scales",
"fable.prophet"
)
install.packages(packages)
library(devtools)
library(ggplot2)
library(dplyr)
library(tsibble)
library(fable)
library(fabletools)
library(feasts)
library(distributional)
library(lubridate)
library(tidyr)
library(forecast)
library(zoo)
library(scales)
library(fable.prophet)
ลองทำงานในตัวอย่าง/โฟลเดอร์เพื่อเริ่มต้น
# Define datapaths
power_consum_path <- "dataset\stunde_2015_2024\Realisierter_Stromverbrauch_201501010000_202407090000_Stunde.csv"
power_consum_smard_prediction_path <- "dataset\propgnose_vom_smard\Prognostizierter_Stromverbrauch_202401010000_202407090000_Stunde.csv"
# Load Smard Prediction
power_consum_smard_prediction_loaded <- load_power_consum(path=power_consum_smard_prediction_path)
raw_smard_pred <- power_consum_smard_prediction_loaded$raw_data
cleaned_smard_pred <- power_consum_smard_prediction_loaded$cleaned_data
cleaned_smard_pred <- cleaned_smard_pred |>
mutate(.model = "SMARD")
names(cleaned_smard_pred)[names(cleaned_smard_pred) == "PowerConsum"] <- ".mean"
# Load PowerConsum Data
power_consum_loaded <- load_power_consum(path=power_consum_path)
raw_power_consum <- power_consum_loaded$raw_data
cleaned_power_consum <- power_consum_loaded$cleaned_data
# Generate more features
cleaned_power_consum$localName[is.na(cleaned_power_consum$localName)] = "Working-Day"
cleaned_power_consum$MeanLastWeek <- rollapply(cleaned_power_consum$PowerConsum, width = 24*8, FUN = function(x) mean(x[1:(24*8-25)]), align = "right", fill = NA)
cleaned_power_consum$MeanLastTwoDays <- rollapply(cleaned_power_consum$PowerConsum, width = 24*3, FUN = function(x) mean(x[1:(24*3-25)]), align = "right", fill = NA)
cleaned_power_consum$MaxLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) max(x[1:(24*2-25)]), align = "right", fill = NA)
cleaned_power_consum$MinLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) min(x[1:(24*2-25)]), align = "right", fill = NA)
คุณลักษณะต่อไปนี้สร้างขึ้นจากชุดข้อมูลและ Holiday API:
| ดัชนี | ชื่อคอลัมน์ | คำอธิบาย |
|---|---|---|
| 1 | วันที่จาก | สำหรับการตรวจสอบความถูกต้องของ DateIndex (คล้ายกัน แต่ดิบ) |
| 2 | พาวเวอร์คอนซัม | การใช้พลังงานในหน่วยเมกะวัตต์ |
| 3 | ดัชนีวันที่ | การประทับเวลา (ปปปป-ดด-วว ชช:นน:วว) |
| 4 | วันธรรมดา | Mo, Di, Mi, Do, Fr, Sa, So (วันธรรมดาเป็นภาษาเยอรมัน) |
| 5 | วันที่ | วันที่ (ปปปป-ดด-วว) |
| 6 | ปี | ปี เย้ |
| 7 | สัปดาห์ | สัปดาห์ที่ 0-53 |
| 8 | ชั่วโมง | เลขที่ชั่วโมง 0-24 |
| 9 | เดือน | เดือนที่ 1-12 |
| 10 | ชื่อท้องถิ่น | ชื่อของวันหยุดสำหรับการประทับเวลา |
| 11 | วันทำงาน | 1/0 ถ้าวันทำงาน (Werktag) แล้ว 1 |
| 12 | โม | 1/0 ถ้าวันจันทร์ก็ 1 |
| 13 | ดิ | 1/0 ถ้าวันอังคารก็ 1 |
| 14 | มิ | 1/0 ถ้าวันพุธก็ 1 |
| 15 | ทำ | 1/0 ถ้าวันพฤหัสบดีก็ 1 |
| 16 | คุณพ่อ | 1/0 ถ้าวันศุกร์ก็ 1 |
| 17 | ส | 1/0 ถ้าวันเสาร์ก็ 1 |
| 18 | ดังนั้น | 1/0 ถ้าวันอาทิตย์ก็ 1 (ไม่จำเป็น ถ้าใช้จันทร์-เสาร์) |
| 19 | วันหยุด | 1/0 หากเป็นวันหยุดก็ให้ 1 |
| 20 | วันทำงานวันหยุดสุดสัปดาห์ | หากเป็นวันหยุด วันหยุดสุดสัปดาห์ หรือวันทำงาน (สำหรับแปลงคือ Char.) |
| 21 | วันหยุดและวันทำงาน | 1/0 หากวันหยุดตรงกับวันทำงานก็จะเป็น 1 |
| 22 | วันสุดท้ายไม่ใช่วันทำงาน | 1/0 ถ้าวันสุดท้ายไม่ใช่วันทำงานก็เท่ากับ 1 |
| 23 | วันสุดท้ายไม่ได้ทำงานและตอนนี้วันทำงาน | 1/0 ถ้าวันสุดท้ายไม่ใช่วันทำงานและตอนนี้เป็นวันทำงานแล้ว 1 |
| 24 | วันถัดไปไม่ทำงานวันและตอนนี้วันทำงาน | 1/0 ถ้าวันถัดไปไม่ใช่วันทำงานและตอนนี้เป็นวันทำงานแล้ว 1 |
| 25 | วันสุดท้ายเป็นวันหยุดและไม่ใช่วันหยุดสุดสัปดาห์ | 1/0 หากวันสุดท้ายเป็นวันหยุดและไม่ใช่วันหยุดสุดสัปดาห์ก็จะเป็น 1 |
| 26 | วันถัดไปเป็นวันหยุดและไม่ใช่วันหยุดสุดสัปดาห์ | 1/0 หากวันถัดไปเป็นวันหยุดและไม่ใช่วันหยุดสุดสัปดาห์ ให้ 1 |
| 27 | ชื่อวันหยุด | คล้ายกับ localName (ชื่อของวันหยุด) |
| 28 | วันสิ้นปี | 1/0 ถ้าเป็นสิ้นปี (สัปดาห์ที่ 52 หรือ 53) |
| 29 | สัปดาห์แรกของปี | 1/0 ถ้าเป็นต้นปี (สัปดาห์ที่ 1) |
| 30 | วันหยุดขยายออกไป | 1/0 วันหยุดล่าช้า (6 ชั่วโมงถึงวันถัดไป) |
| 31 | วันหยุดเรียบ | HolidayExtend + sin(2*pi(ชั่วโมง)+1)/24) |
| 32 | หมายความว่าสัปดาห์ที่แล้ว | ค่าเฉลี่ยกำลังการบริโภคของสัปดาห์ที่แล้ว (กะ: 24*8-25) |
| 33 | MeanLastTwoDays | Mean PowerConsum ของสองวันที่ผ่านมา (Shift: 24*3-25) |
| 34 | MaxLastOneDay | Max PowerConsum ของวันสุดท้าย (Shift: 24*2-25) |
| 35 | นาทีสุดท้ายหนึ่งวัน | ปริมาณการใช้พลังงานขั้นต่ำของวันสุดท้าย (Shift: 24*2-25) |
ในการศึกษานี้มีชุดข้อมูลการใช้พลังงานในประเทศเยอรมนีจาก SMARD ปี 2015 - 2024
รูปที่ 1 แสดงชุดข้อมูลดิบที่มีค่าหายไป (สีแดง) การประทับเวลาซ้ำ (สีแดงเข้ม) และการใช้พลังงานเมื่อเวลาผ่านไป (สีเทา) ความละเอียดรายชั่วโมง ด้วยค่าที่หายไปหนึ่งค่าและค่าซ้ำอีกหนึ่งค่าทุกปี จึงทำให้ง่ายต่อการล้างชุดข้อมูล โดยรวมแล้วเป็นชุดที่เกือบสะอาด หลังจากล้างชุดข้อมูลแล้ว จะมีการสังเกตที่เป็นไปได้สำหรับการใช้พลังงาน:
มีวิธีง่ายๆ ในการเติมเต็มช่องว่างด้วยการสังเกตครั้งสุดท้าย (เป็นไปได้ เนื่องจากความละเอียดมีขนาดใหญ่เพียงพอ และเนื่องจากมีค่าที่ขาดหายไปเพียงไม่กี่ค่า) ค่าแรกถูกเก็บไว้สำหรับการทำซ้ำ
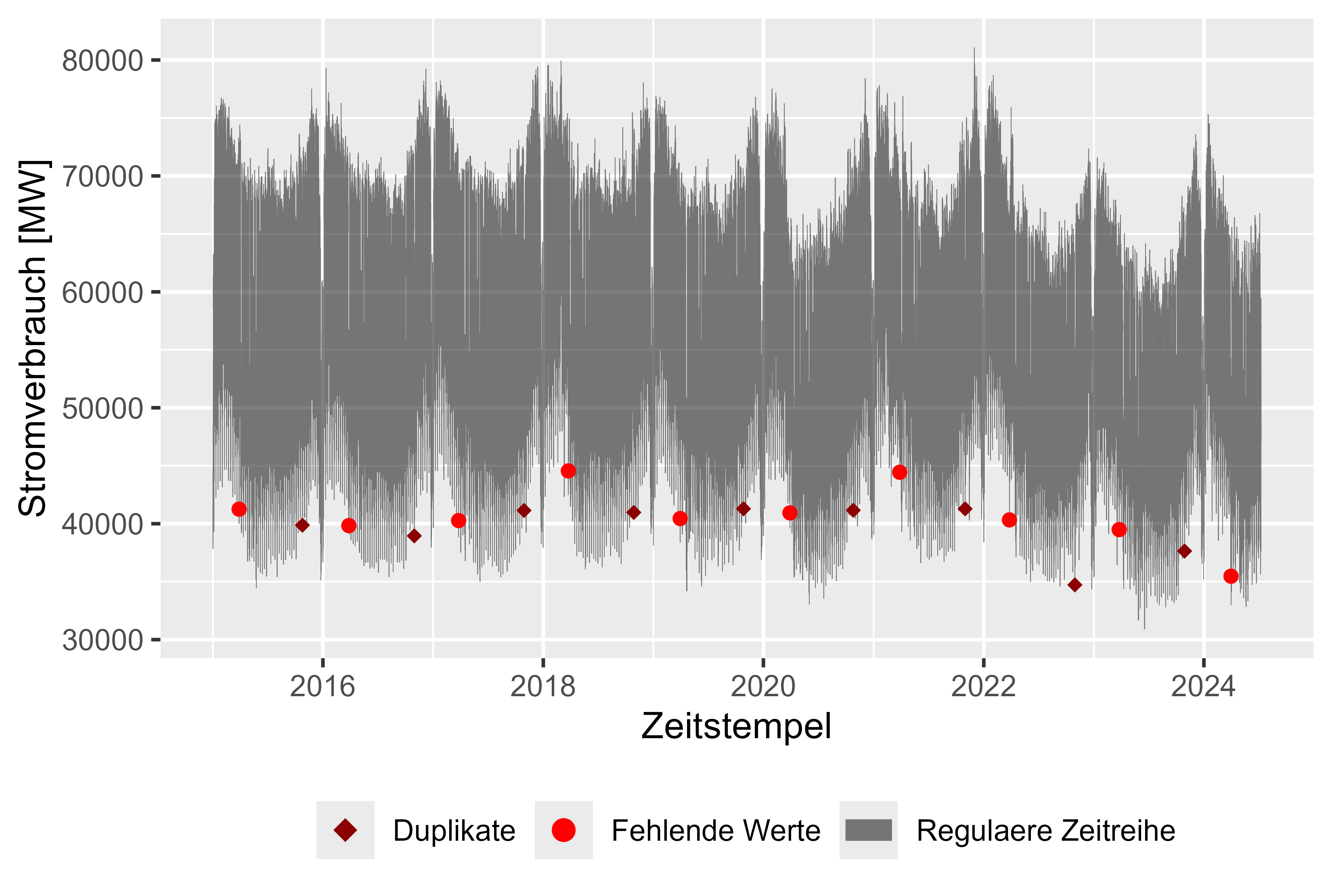รูปที่ 1 การใช้พลังงานดิบ
local_name_colors <- c(
"Christi Himmelfahrt" = palette()[2],
"Erster Weihnachtstag" = palette()[2],
"Karfreitag" = palette()[2],
"Neujahr" = palette()[2],
"Ostermontag" = palette()[2],
"Pfingstmontag" = palette()[2],
"Reformationstag" = palette()[2],
"Tag der Arbeit" = palette()[2],
"Tag der Deutschen Einheit" = palette()[2],
"Zweiter Weihnachtstag" = palette()[2],
"Regulärer Tag" = palette()[1]
)
week_colors <- c(
"Mo" = palette()[1],
"Di" = palette()[1],
"Mi" = palette()[1],
"Do" = palette()[1],
"Fr" = palette()[1],
"Sa" = palette()[2],
"So" = palette()[2]
)
working_colors <- c("1" = "#2E9FDF", "0" = "#FC4E07")
whw_colors <- c(
"FeiertagnKein Wochenende" = "black",
"Kein FeiertagnKein Wochenende" = "red",
"Kein FeiertagnWochenende" = "orange",
"FeiertagnWochenende" = "blue"
)
p <- cleaned_power_consum |>
gg_tsdisplay(PowerConsum, plot_type = "partial", lag = 100)
ggsave(
"plots/power_consum_acf_pacf.png",
plot = p,
width = 5.5,
height = 3.7,
dpi = 600
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MinLastOneDay.png",
x = "MinLastOneDay",
y = "PowerConsum",
x_label = "Minimaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MaxLastOneDay.png",
x = "MaxLastOneDay",
y = "PowerConsum",
x_label = "Maximaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastWeek.png",
x = "MeanLastWeek",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 7 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastTwoDays.png",
x = "MeanLastTwoDays",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 2 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkdayHolidayWeekend",
file_name = "plots\workday_holiday_weekend_histogram.png",
colors = whw_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "Holiday",
file_name = "plots\holiday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Werktag oder Wochenende",
name_1 = "Feiertag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "HolidayAndWorkDay",
file_name = "plots\holiday_workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Werktag",
name_1 = "Feiertag am Werktag"
)
plot_by_group(
cleaned_power_consum,
group_name = "HolidayName",
file_name = "plots\holiday_boxplot.png",
colors = local_name_colors,
title = "Übersicht der einzelnen Feiertage",
y="PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "Weekday",
file_name = "plots\weekday_boxplot.png",
colors = week_colors,
title = "Übersicht der einzelnen Wochentage",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_boxplot.png",
colors = working_colors,
title = "Übersicht, ob Feiertag (FALSE) oder Werktag (TRUE)",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_column(
df = cleaned_power_consum,
x = "Hour",
y = "PowerConsum",
x_label = "Stunden",
y_label = "Stromverbrauch [MW]",
file_name = "plots\hour_boxplot.png",
title = "Übersicht der einzelnen Stunden"
)
plot_by_column(
df = cleaned_power_consum,
x = "Month",
y = "PowerConsum",
x_label = "Monate",
y_label = "Stromverbrauch [MW]",
file_name = "plots\month_boxplot.png",
title = "Übersicht der einzelnen Monate"
)
plot_by_column(
df = cleaned_power_consum,
x = "Week",
y = "PowerConsum",
x_label = "Woche",
y_label = "Stromverbrauch [MW]",
file_name = "plots\week_boxplot.png",
title = "Übersicht der einzelnen Wochen"
)
plot_by_column(
df = cleaned_power_consum,
x = "Year",
y = "PowerConsum",
x_label = "Jahr",
y_label = "Stromverbrauch [MW]",
file_name = "plots\year_boxplot.png",
title = "Übersicht der einzelnen Jahre"
)
plot_year_month_week_day(
df=cleaned_power_consum,
date_column="DateIndex",
y="PowerConsum",
from_year=2015,
to_year=2024,
from_week=0,
to_week=53,
year_for_week=2018,
from_day=1,
to_day=30,
month_for_day=4,
year_for_day=2018,
from_month=1,
to_month=12,
year_for_month=2018,
holiday="Holiday",
day_of_week = "Weekday"
)
ส่วนต่อไปนี้จะกล่าวถึงรายละเอียดของข้อมูลมากขึ้นเรื่อยๆ เราจะเริ่มต้นที่นี่ด้วยการเป็นตัวแทนประจำปี
รูปที่ 2 เป็นตัวแทนรายปีของปี 2558-2567 เราจะสังเกตเห็นได้ว่าในช่วงต้นปีมีการใช้พลังงานเพิ่มขึ้น และในช่วงปลายปีมีการลดลง (คริสต์มาส ปีใหม่) โดยรวมแล้วจะมีลักษณะเป็นรูปยิ้มหรือโค้งคำนับ
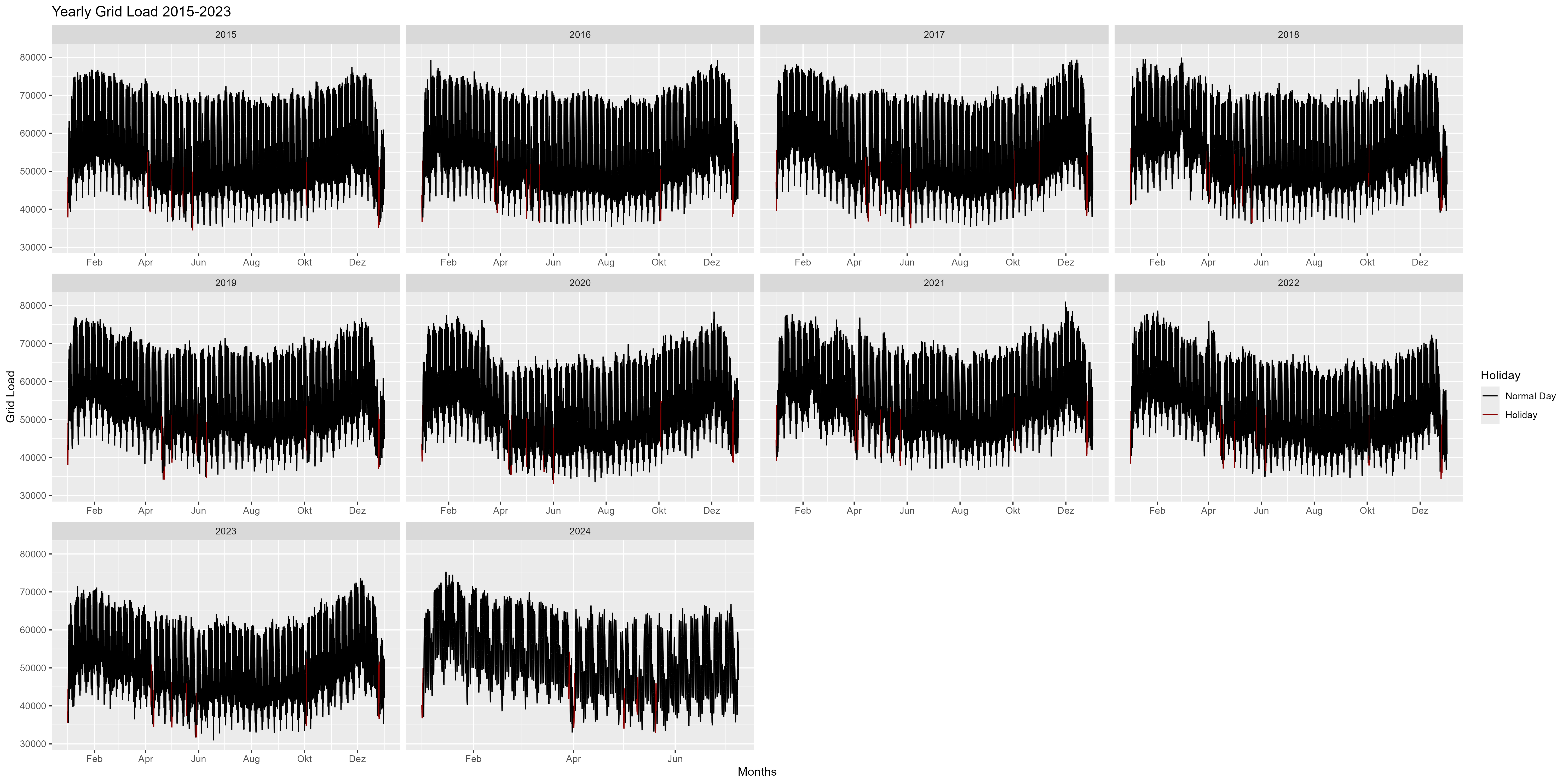รูปที่ 2 การใช้พลังงานด้านเดียวทุกปี
ลองรวมปีทั้งหมดแล้วแบ่งออกเป็นสัปดาห์ Boxplots ในรูปที่ 3 รวมกันทุกปี เราจะเห็นรูปแบบได้ละเอียดยิ่งขึ้น เริ่มต้นและสิ้นปีจะแสดงด้วยสีแดง และแสดงการลดลงจาก "รูปร่างยิ้ม" ตามปกติ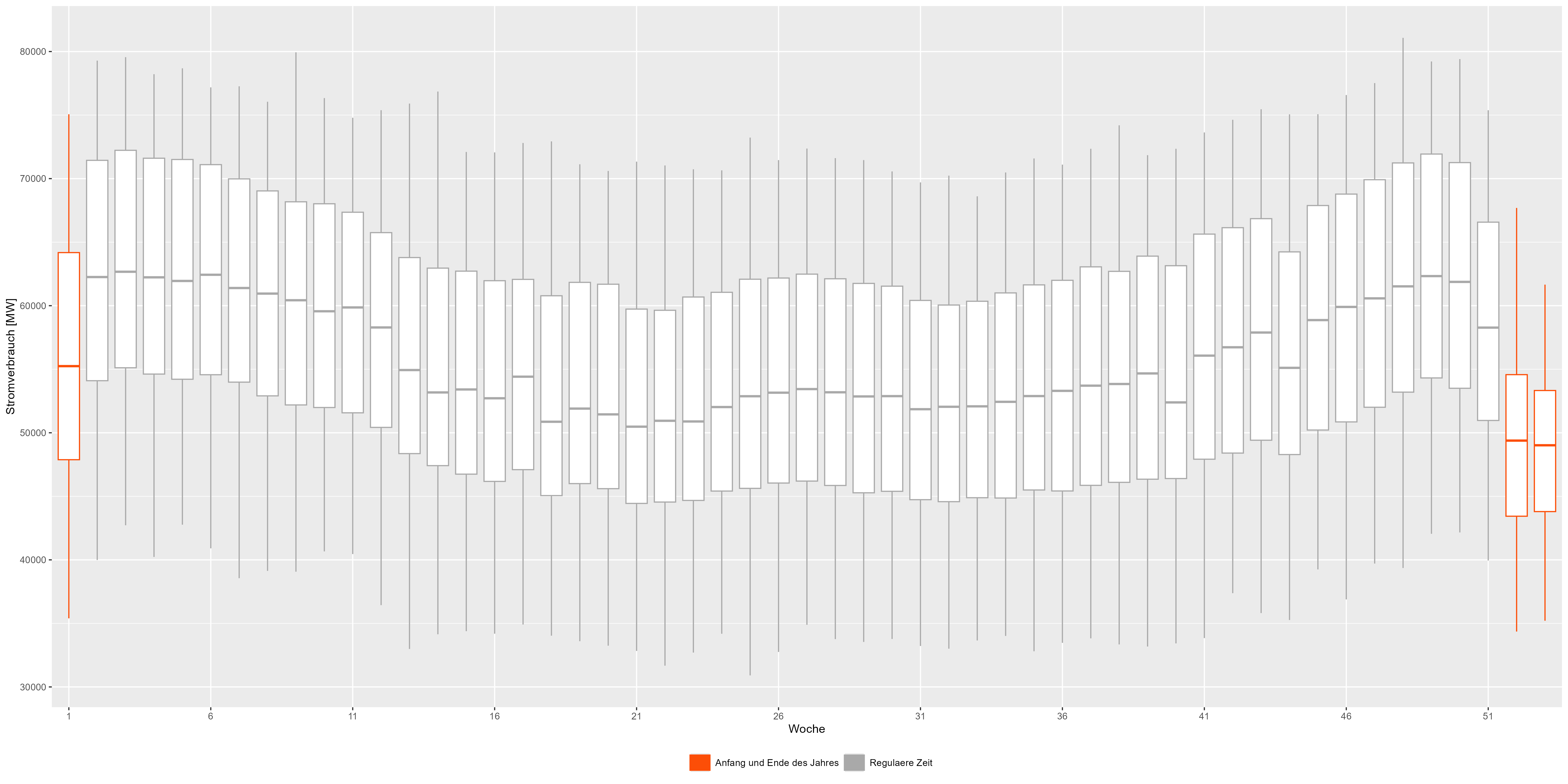
รูปที่ 3 การใช้พลังงานข้อมูลรวมรายสัปดาห์
เรามาดูรายละเอียดเพิ่มเติมและดูในปี 2018 เป็นตัวอย่าง รูปที่ 4 คือการแสดงรายเดือนของปี 2018 เราจะดูรายละเอียดเพิ่มเติมในช่วงปลายปีได้ที่นี่ ประมาณวันที่ 24 ธันวาคม มีการใช้พลังงานลดลง ที่น่าสังเกตอีกอย่างคือวันหยุดสุดสัปดาห์และวันหยุดนักขัตฤกษ์ (สีแดง) ลดลงสำหรับทุกสุดสัปดาห์และทุกวันหยุด
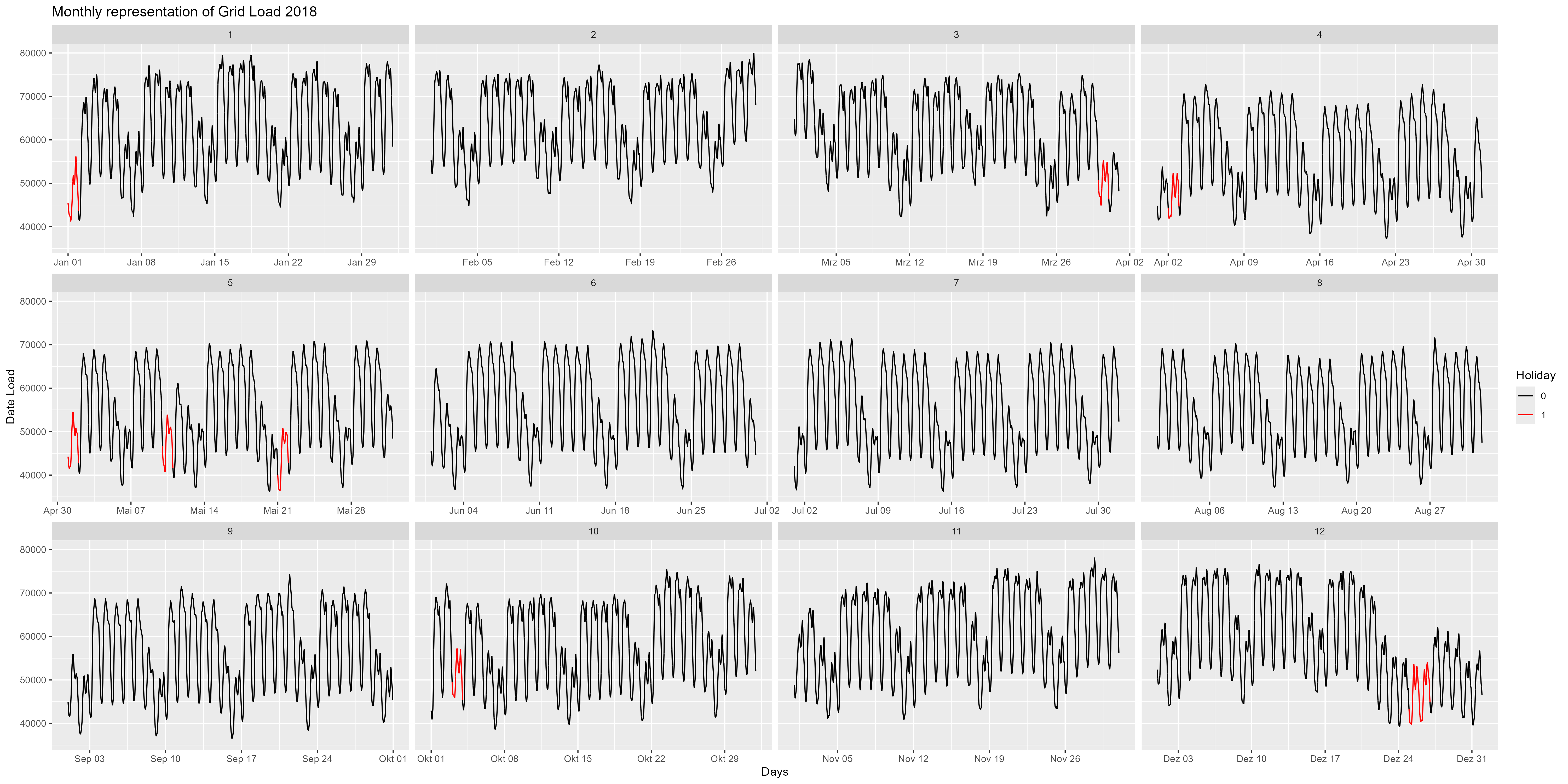รูปที่ 4 การใช้พลังงานทุกเดือนเป็นด้านเดียว
เราสามารถไปไกลกว่านี้ได้และตรวจสอบการแสดงข้อมูลรายชั่วโมง รูปที่ 5 แสดง Boxplot รวมทุกชั่วโมง นอกจากนี้ยังมีเวลากลางคืนลดลง (21.00-06.00 น.) และช่วงเวลากลางวัน/เวลาทำงานเพิ่มขึ้น (06.00-21.00 น.) รวมถึงรูปแบบที่ต้องรวมไว้ในโมเดลด้วย
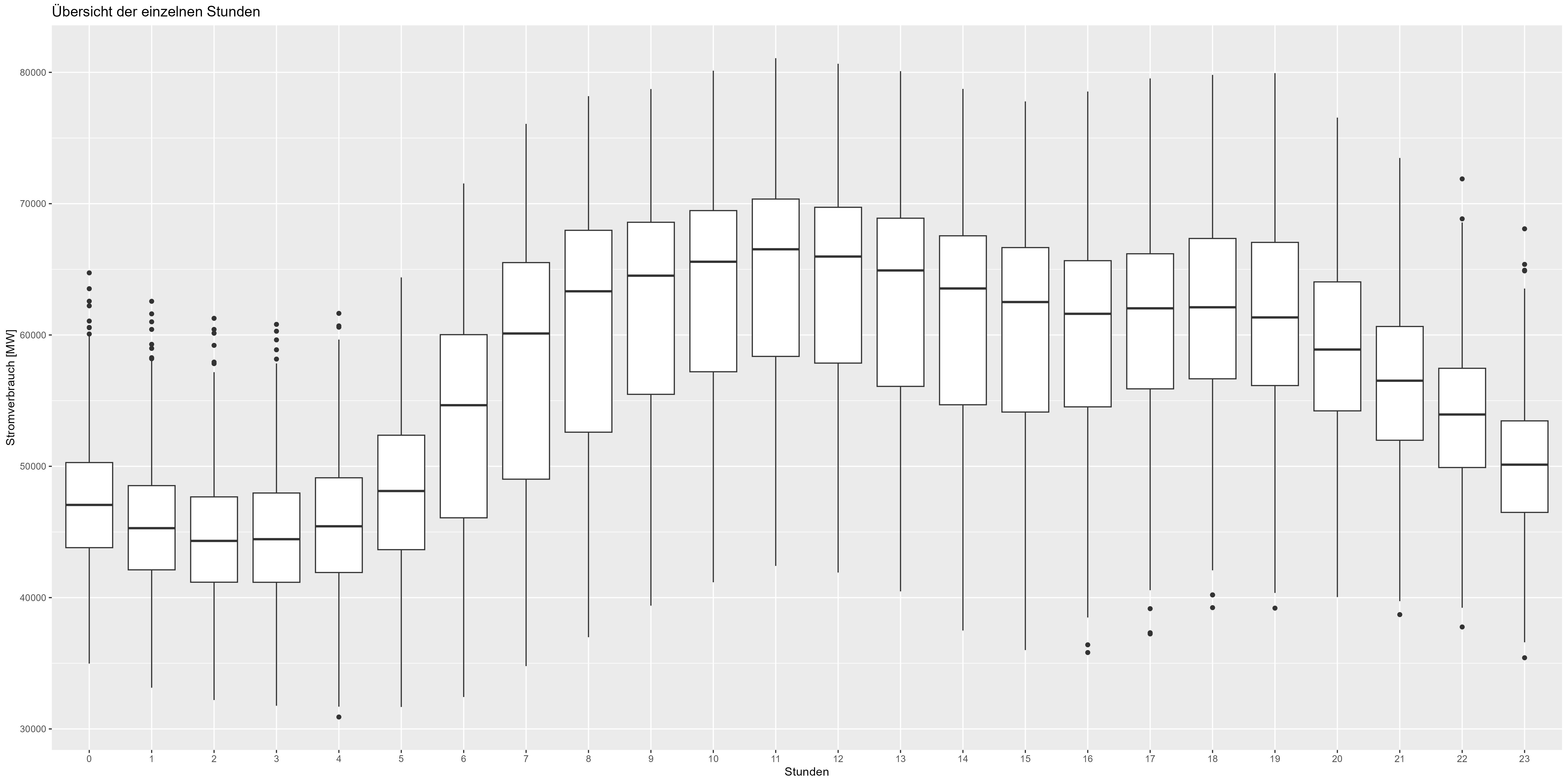รูปที่ 5 การใช้พลังงานข้อมูลรวมรายชั่วโมง
มาพูดถึงวันธรรมดากันดีกว่า ตามที่คาดไว้ในช่วงสุดสัปดาห์ การใช้พลังงานลดลง "Durchschnitt" คือค่าเฉลี่ย รูปที่ 6 แสดงวันธรรมดาทั้งหมด (รวม) ในช่วงหลายปีที่ผ่านมา มีการลดลงประมาณ 10,000 MW ในช่วงสุดสัปดาห์
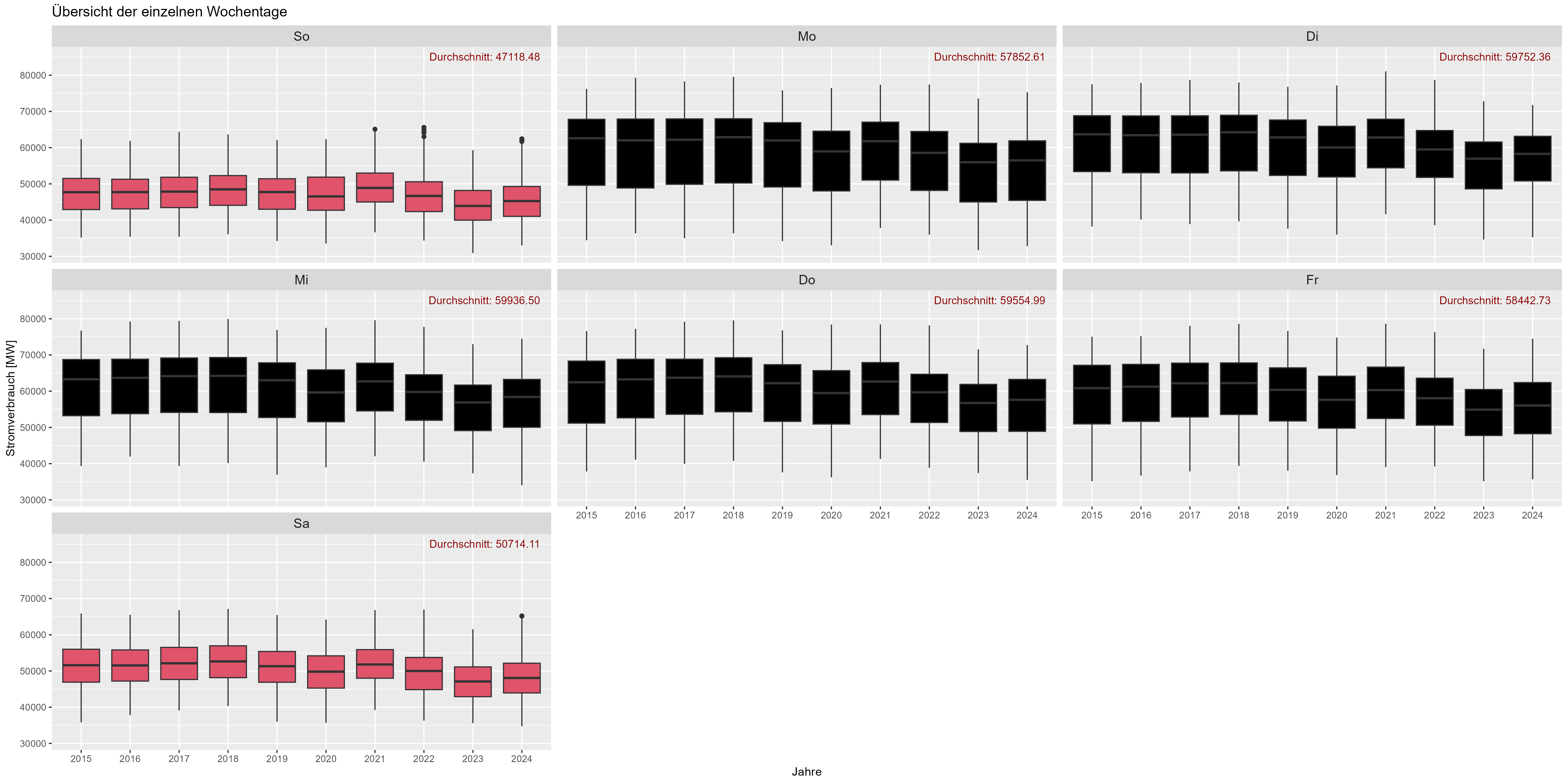รูปที่ 6 การใช้พลังงาน "ผลกระทบวันในสัปดาห์"
รูปที่ 8 แสดงผลวันหยุด "Durchschnitt" คือการใช้พลังงานเฉลี่ยตลอดหลายปีที่ผ่านมา มีการใช้พลังงานเพิ่มขึ้นอย่างมากสำหรับ "วันทำงาน" (สีเทาเข้ม) เมื่อเทียบกับวันหยุด (สีแดง) เราสามารถสรุปได้ว่าวันหยุดก็เหมือนกับวันหยุดสุดสัปดาห์สำหรับการใช้พลังงาน"
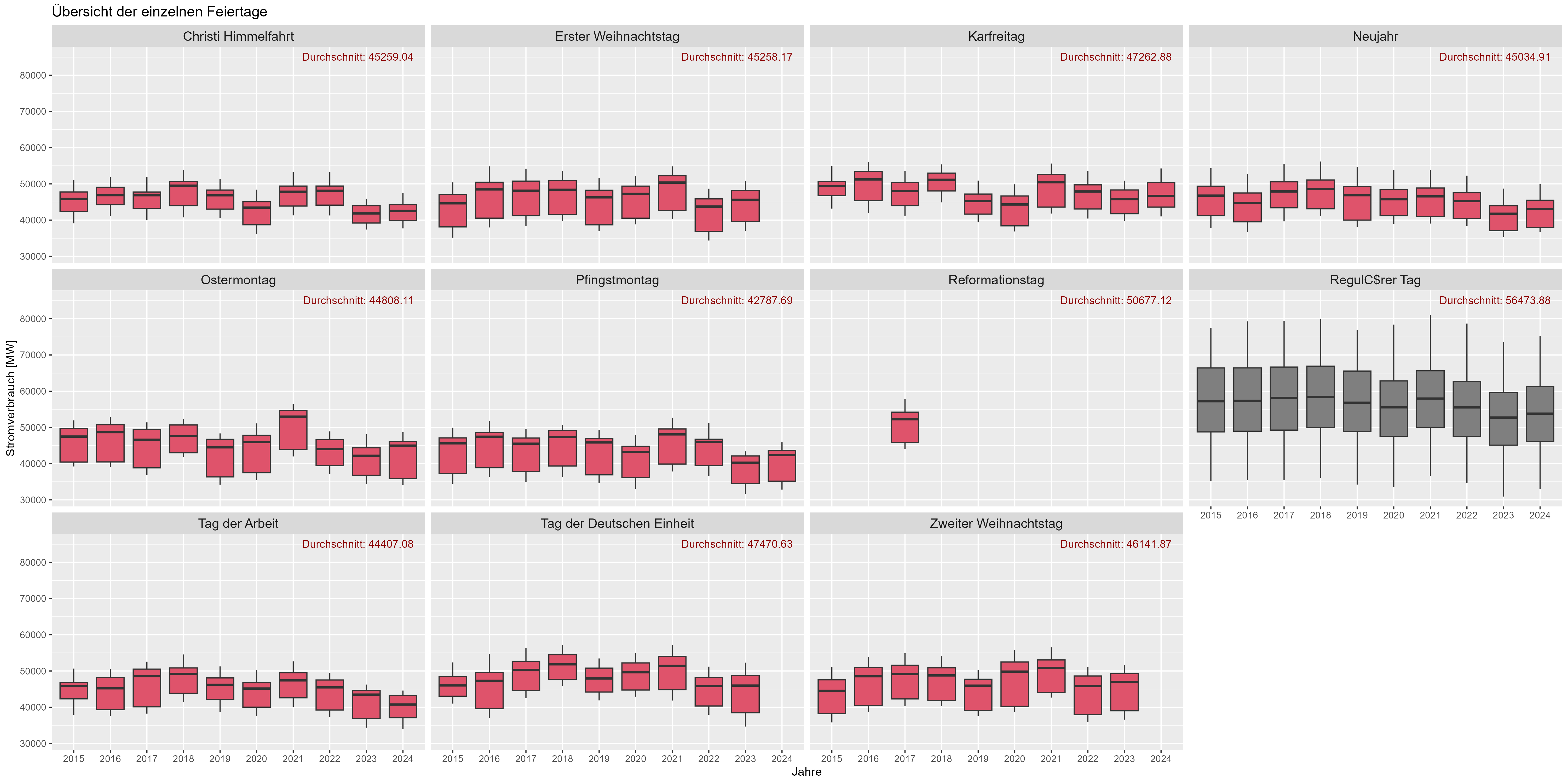รูปที่ 6 การใช้พลังงาน "ผลวันหยุด"
รูปที่ 7 แสดงถึงพฤติกรรมที่แตกต่างกันในแต่ละวัน มี 4 หมวด "Feiertag Kein Wochenende" แปลว่าเป็นวันหยุด แต่ไม่ใช่วันหยุดสุดสัปดาห์ "Feiertag Wochenende" หมายความว่าเป็นวันหยุดและวันหยุดสุดสัปดาห์ "Kein Feiertag Kein Wochenende" หมายความว่าเป็นวันทำงานปกติ และ "Kein Feiertag Wochenende" หมายความว่าเป็นเพียงวันหยุดสุดสัปดาห์ เราสามารถสังเกตการแจกแจงที่คล้ายกันสำหรับวันทำงานที่ ไม่ใช่ ปกติตามที่สันนิษฐานไว้
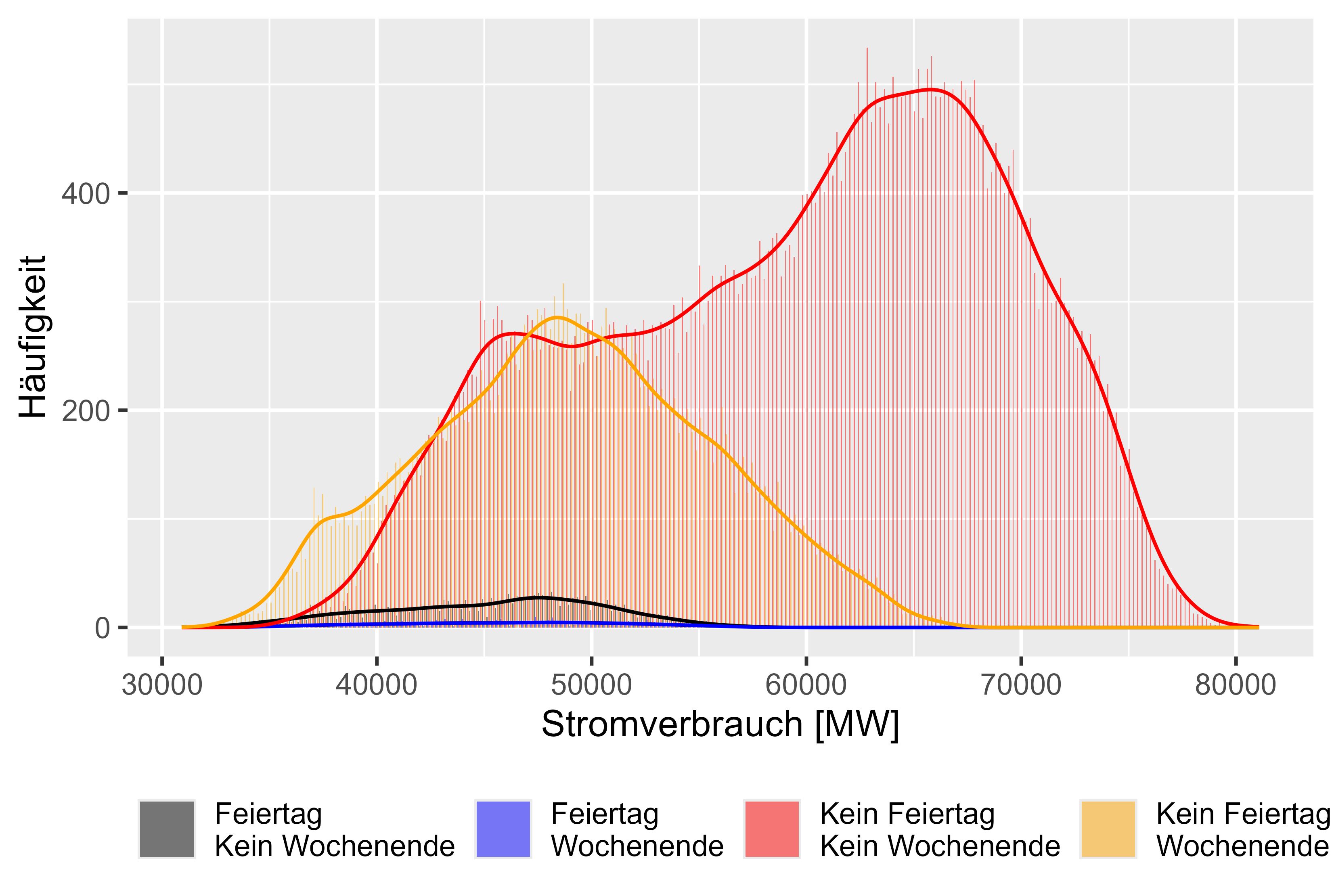รูปที่ 7 การใช้พลังงาน "ผลต่าง" เปรียบเทียบ
ค่าที่ล่าช้า เช่น MeanLastTwoDays, MeanLastWeek, MaxLastOneDay และ MinLastOneDay เป็นคุณลักษณะที่สร้างขึ้น
คล้ายกับที่กล่าวไว้ใน DOI: 10.1109/TPWRS.2011.2162082 - การพยากรณ์โหลดระยะสั้นโดยอิงตามแบบจำลองการเติมสารกึ่งพารามิเตอร์
รูปที่ 8-11 (สีแดงไม่ใช่วันทำการ) แสดงถึงค่าที่ล่าช้านี้เทียบกับการใช้พลังงานจริง
มีความสัมพันธ์กันเล็กน้อยสำหรับคุณลักษณะที่สร้างขึ้นนี้
# Check Correlation
cor <- cor(cleaned_power_consum[sapply(cleaned_power_consum, is.numeric)], method = c("pearson", "kendall", "spearman"), use = "complete.obs")
| คุณสมบัติ | ความสัมพันธ์กับ PowerConsum |
|---|---|
| วันหยุดเรียบ | -0.556194 |
| หมายความว่าสัปดาห์ที่แล้ว | 0.389044 |
| MeanLastTwoDays | 0.201253 |
| MaxLastOneDay | 0.320193 |
| นาทีสุดท้ายหนึ่งวัน | 0.348583 |
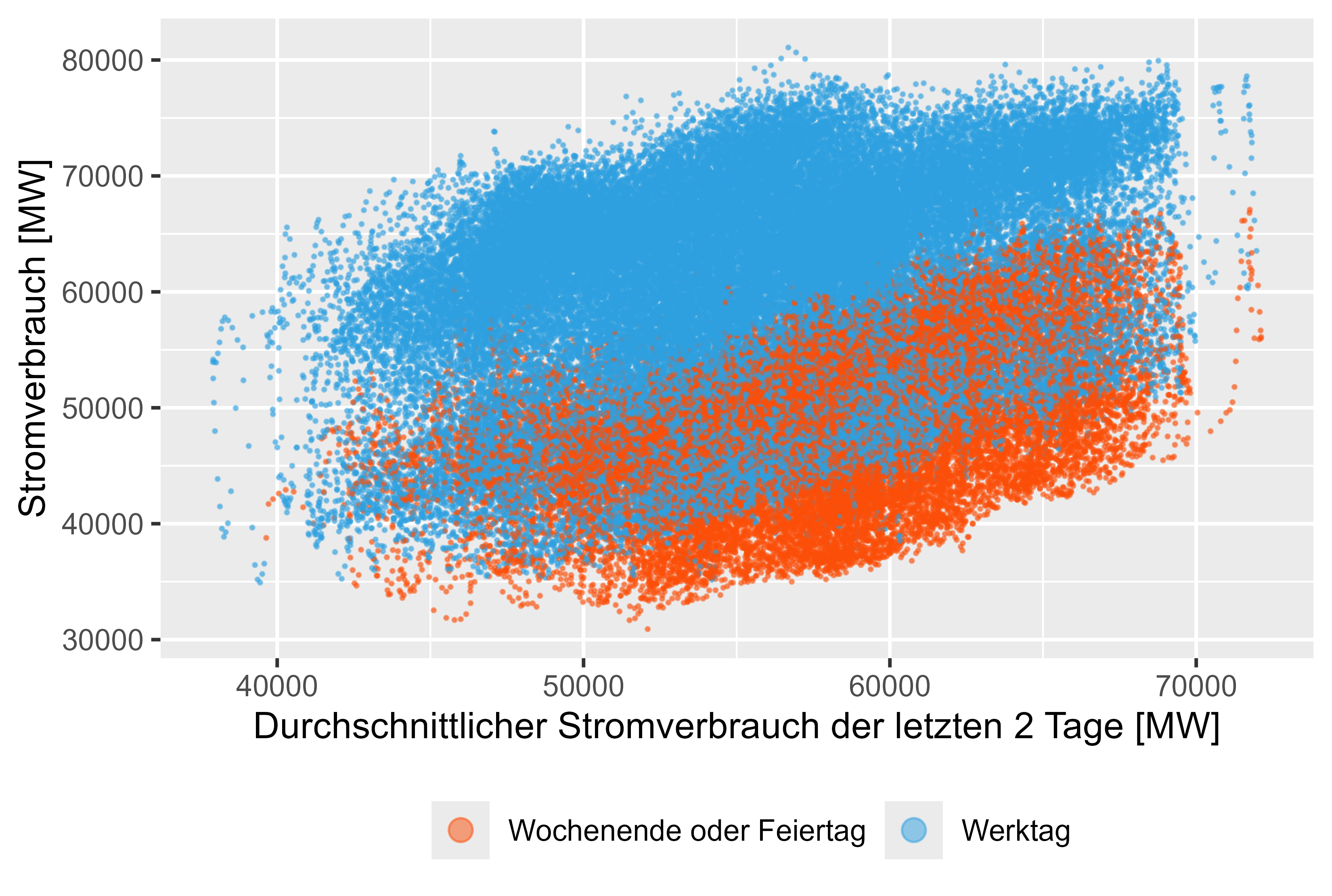รูปที่ 8 การใช้พลังงาน - MeanLastTwoDays
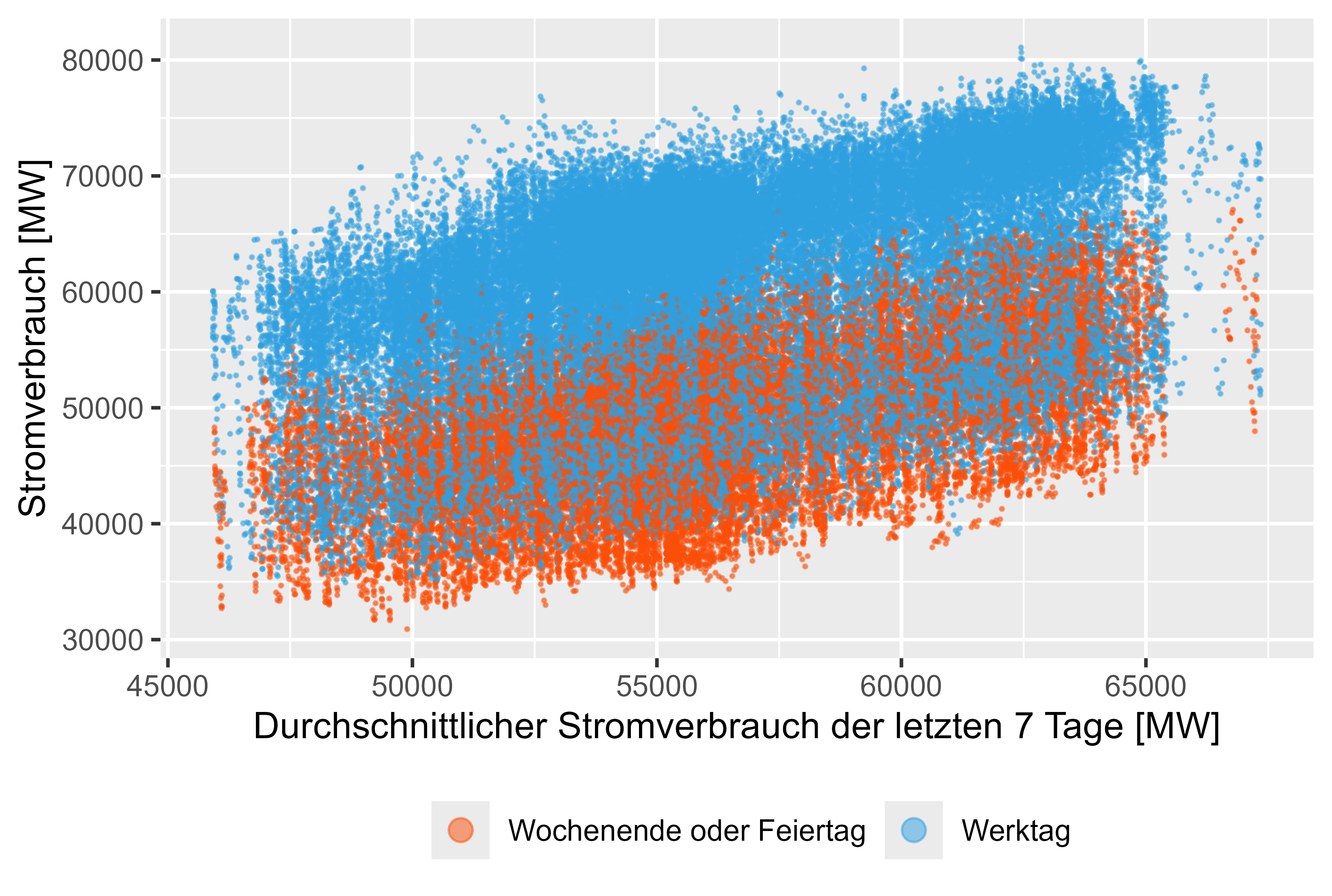รูปที่ 9 การใช้พลังงาน - MeanLastWeek
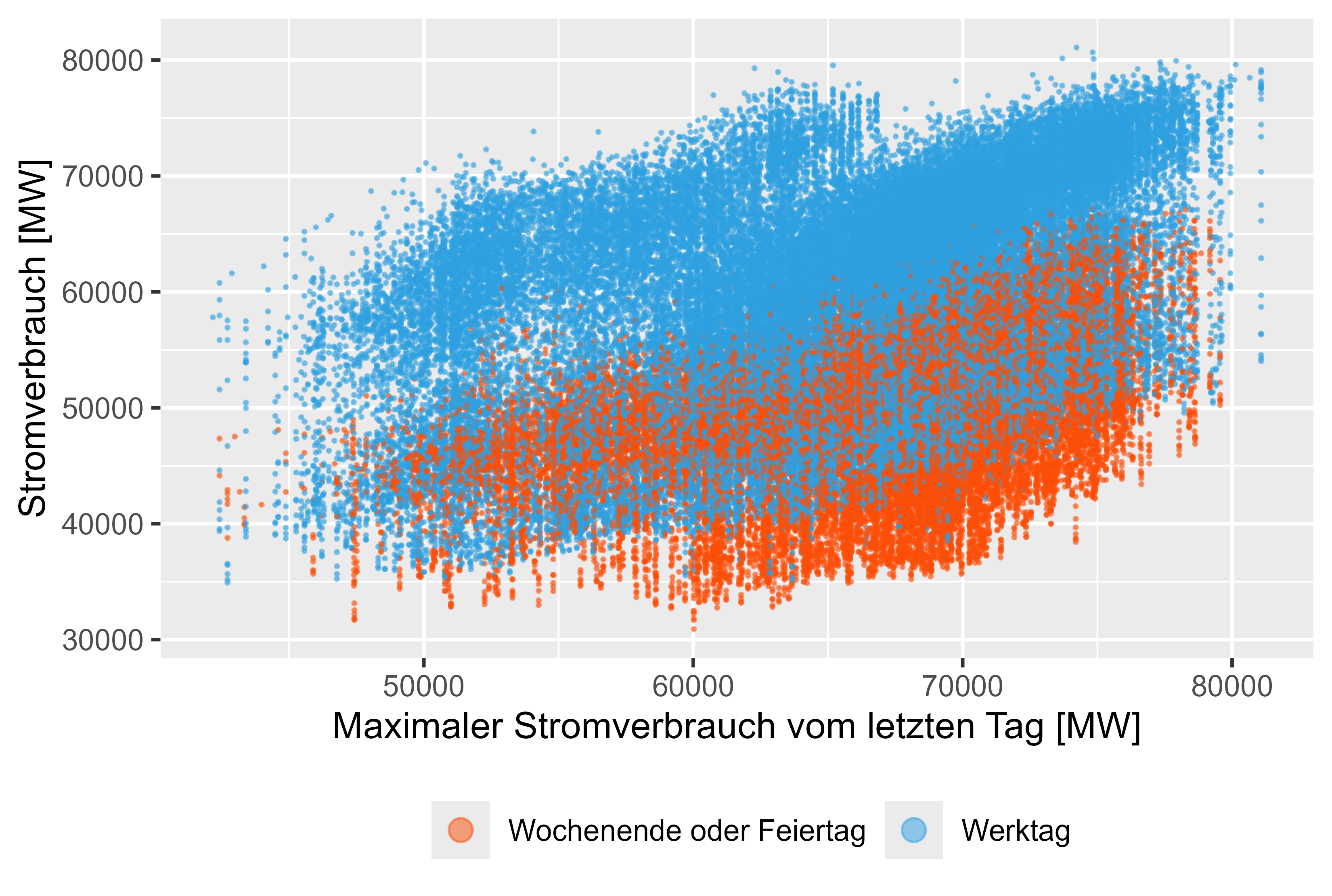รูปที่ 10 การใช้พลังงาน - MaxLastOneDay
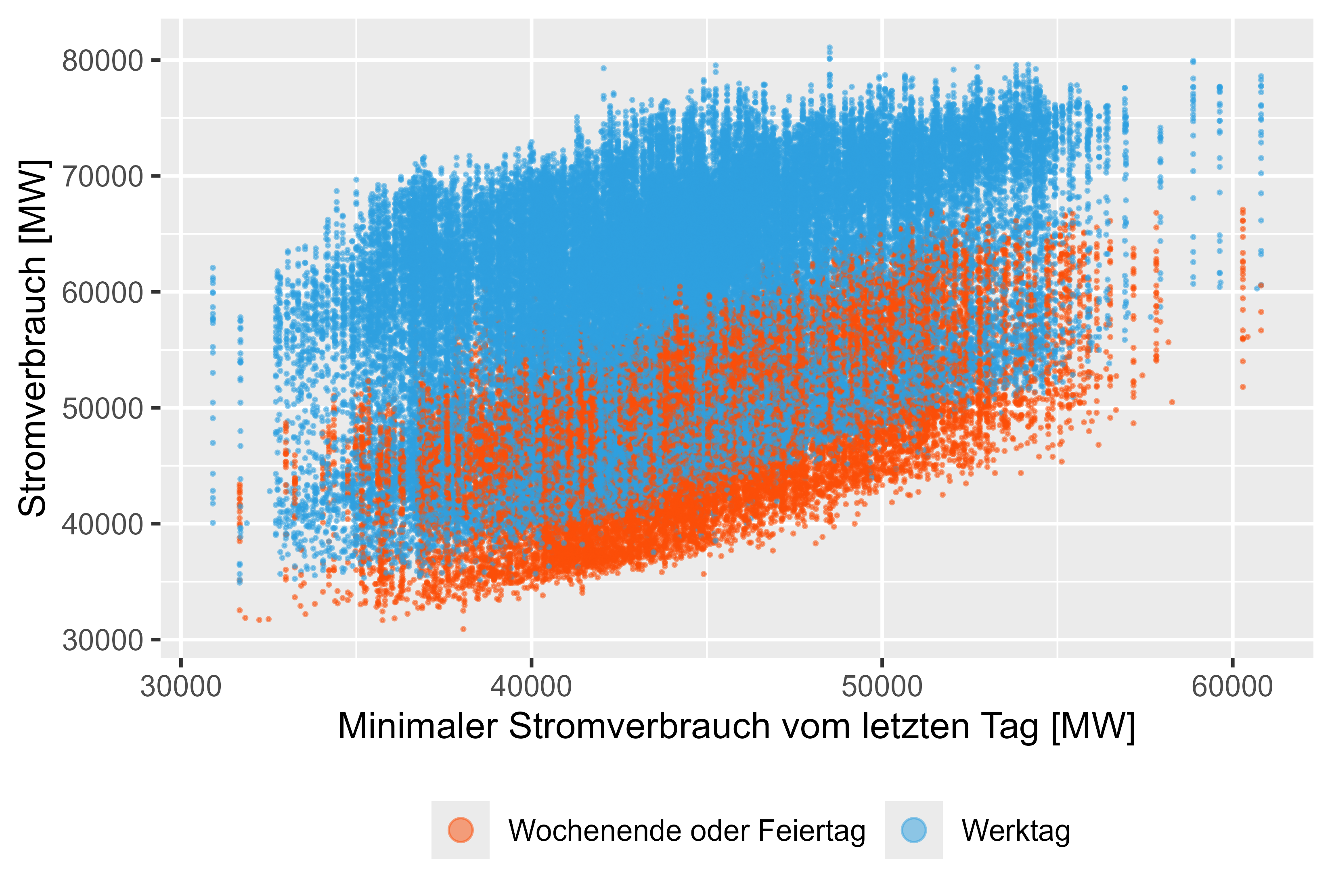รูปที่ 11 การใช้พลังงาน - MinLastOneDay
มีฤดูกาลที่ซับซ้อน สำหรับการแก้ไขรายชั่วโมงจะมีตามฤดูกาลเป็นรายปี รายสัปดาห์ และรายวัน ซึ่งจะต้องมีการติดตามตามโมเดล วิธีแก้ปัญหานี้เป็นไปตามที่กล่าวไว้ใน การพยากรณ์: หลักการและการปฏิบัติ บทที่ 12.1 ฤดูกาลที่ซับซ้อนเพื่อใช้เงื่อนไขที่สี่เพื่อนำเสนอและประกอบผ่าน cos() และ sin() ฤดูกาลที่ซับซ้อน
เราสามารถพิจารณาพล็อต ACF และ PACF เพียงเล็กน้อย โดยมีการเพิ่มขึ้นที่มีนัยสำคัญเล็กน้อย แต่เป็นเพียงการแสดงค่าที่ล่าช้า 96 ค่า หากเราใช้การสังเกตที่ล่าช้าประมาณ 9,000 ครั้งเป็นเวลาหนึ่งปี ฤดูกาลจะมีความซับซ้อน นั่นเป็นเหตุผลว่าทำไมการใช้เทอมสี่เรียร์จึงง่ายกว่า มันยังทำงานได้ไม่ดีนักเพียงแค่ค้นหาส่วนประกอบ PDQ และ pdq ด้วย
ARIMA(...
stepwise=FALSE,
greedy=FALSE,
approx=FALSE)
ตัวมันเอง นอกจากนี้เวลาในการฝึกอบรมยังเพิ่มขึ้นอย่างมากโดยไม่มีเงื่อนไขที่สี่
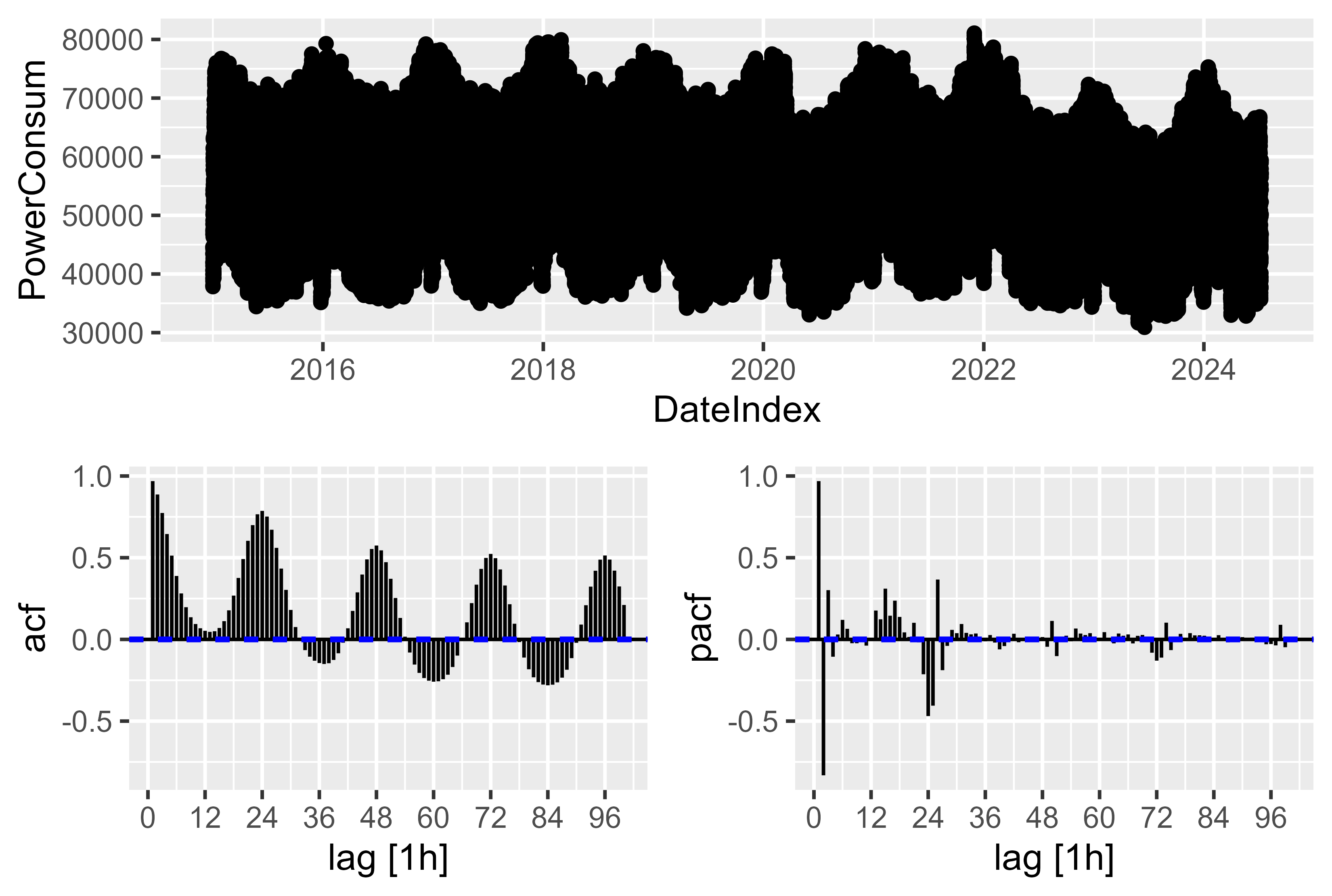รูปที่ 12 การใช้พลังงาน - ACF PACF แผนการใช้พลังงานดิบ
การผสมผสานคุณสมบัติที่ดีที่สุดในงานนี้คือ:
เพื่อเปรียบเทียบแบบจำลองที่เราใช้เมตริก MAE และ MAPE SMARD เป็นโมเดลของ "Bundesnetzagentur" จากเพจ SMARD แบบจำลองศาสดาพยากรณ์ก็ทดลองใช้เช่นกัน ทำได้ดี แต่ยังไม่ดีพอ
ค่าพยากรณ์ SMARD ถึง MAPE ที่ 3.6% <- ไม่ได้อยู่ในการศึกษานี้
ข้อมูลการฝึกอบรม:
โมเดลที่ดีที่สุดที่พบจนถึงสงคราม LHM + DHR (linear-harmonic-model + dynamic-harmonic-regression)
แนวคิดคือการรวมโมเดลเชิงเส้นเข้ากับโมเดล ARIMA เพราะมันเป็นเรื่องยากสำหรับโมเดล ARIMA ที่จะจัดการกับตัวแปรจำลองสำหรับวันหยุด ดังนั้นนางแบบทั้งมวลจึงช่วยออกมา
train_power_consum <- cleaned_power_consum |>
filter(year(DateIndex) > 2020 & (year(DateIndex) < 2024))
generate_models(model_name = "model/mean_naive_drift",
train_power_consum = train_power_consum)
train_power_consum_v5 <- train_power_consum |>
mutate(HolidaySmoothed = Holiday + sin(2 * pi * (as.numeric(Hour)+1) / 24))
holiday_effect_model <- lm(
PowerConsum ~
HolidaySmoothed,
data = train_power_consum_v5
)
saveRDS(holiday_effect_model, file = "ensemble_model/version_5/holiday_effect_2021_2023.rds")
train_power_consum_v5$Residuals <- residuals(holiday_effect_model)
fit <- train_power_consum_v5 |>
model(
ARIMA = ARIMA(Residuals ~
PDQ(0,0,0)
+ pdq(d=0)
+ MeanLastWeek
+ WorkDay
+ EndOfTheYear # new
+ FirstWeekOfTheYear # new
+ MeanLastTwoDays
+ MaxLastOneDay
+ MinLastOneDay
+ fourier(period = "day", K = 6)
+ fourier(period = "week", K = 7)
+ fourier(period = "year", K = 3)
)
)
saveRDS(fit, file = "ensemble_model/version_5/arima_2021_2023.rds")
เราสามารถเห็นภาพเอฟเฟกต์และวิธีการทำงานของโมเดลได้ รูปที่ 13 แสดงแนวคิดเบื้องหลังโมเดลนี้ ก่อนอื่น เราปรับแบบจำลอง LHM ให้เหมาะสมและคำนวณส่วนที่เหลือ ฝึกแบบจำลอง DHR ตามส่วนที่เหลือและสรุปทั้งสองอย่าง มันเป็นเหมือนกระจกเงาบน LHM และดันค่ากลับไปด้านบน
สำหรับโมเดล LHM เราใช้แนวทางง่ายๆ ในการสร้างกราฟไซนัสซึ่งทำซ้ำทุกๆ 24 ชั่วโมง และลดลงหรือเพิ่มขึ้นในวันหยุดหรือวันทำงาน
ด้วยการคาดการณ์ LHM จากข้อมูลใหม่ เราสามารถคาดการณ์ปริมาณคงเหลือสำหรับข้อมูลใหม่ได้ Residuals + LHM เลื่อนค่ากลับไปยังตำแหน่ง "ถูกต้อง"
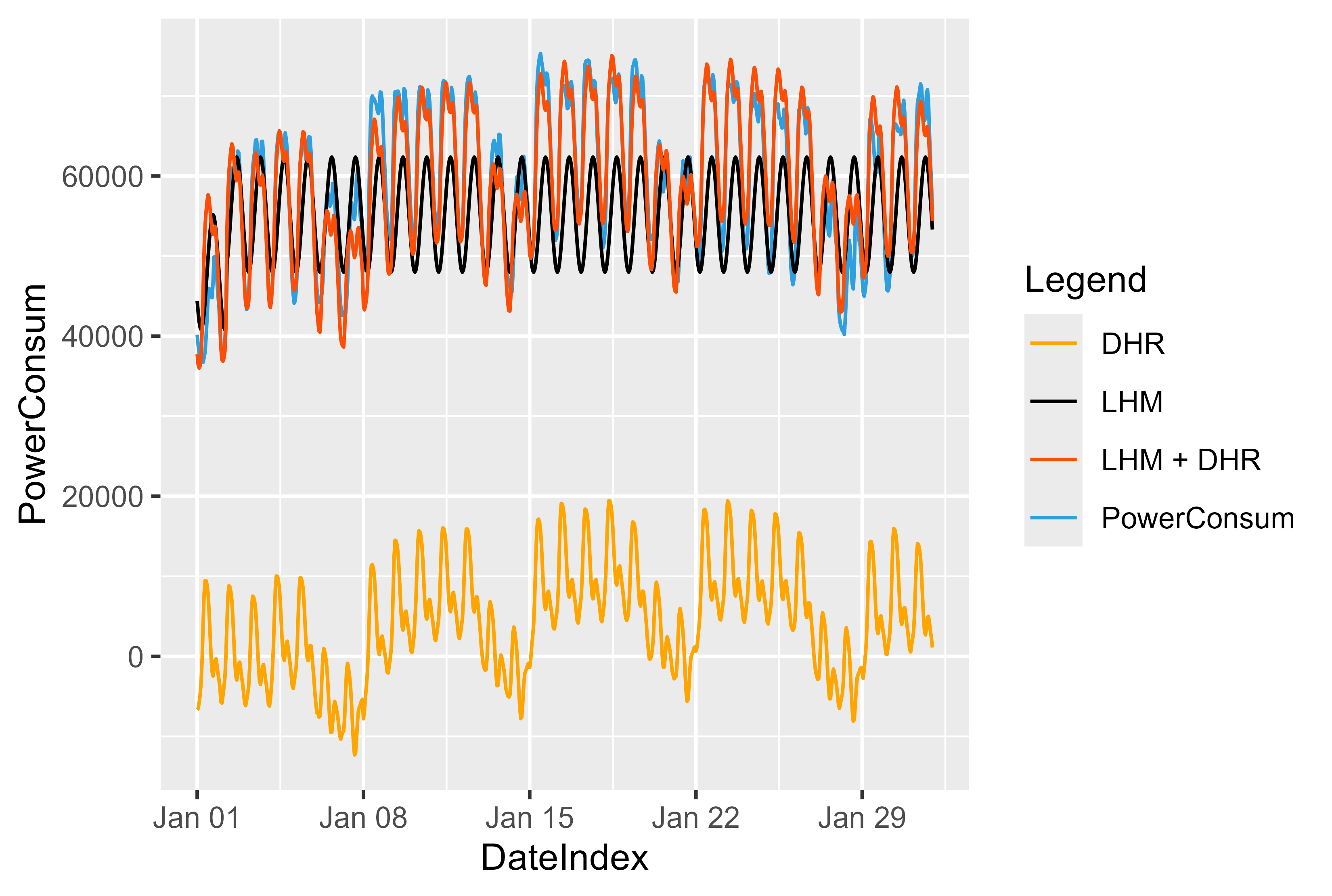รูปที่ 13 การแสดงโมเดล LHM + DHR
ensembled_fc <- load_ensembled_models(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
real_data = cleaned_power_consum,
smard_fc = cleaned_smard_pred,
model_path = "ensemble_model"
)
all_forecasts_ensembled <- ensembled_fc$all_forecasts
raw_fc_ensembled <- ensembled_fc$raw_forecasts
fc <- load_all_model_results(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
smard_fc = cleaned_smard_pred,
real_data = cleaned_power_consum
)
all_forecasts <- fc$combined_forecasts
raw_fc <- fc$raw_forecasts
metric_results <- calculate_metrics(fc_data = all_forecasts, fc_data_ensembled=all_forecasts_ensembled)
# Plot best Model for single Models
name_of_best_model_for_single_model <- plot_forecast(
all_forecasts = all_forecasts,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
raw_fc = raw_fc,
month_to_plot = 1,
days_to_plot = 40
)
# Plot best Model for ensembled Models
name_of_best_model_ensembled <- plot_forecast_ensembled(
all_forecasts = all_forecasts_ensembled,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
month_to_plot = 1,
days_to_plot = 40
)
# Residuals Compared with SMARD
plot_compare_with_smard(
all_forecasts = all_forecasts_ensembled,
name_of_best_model = name_of_best_model_ensembled
)
# LHM DHM representation
plot_representation_of_lhm_dhm_components(path_dhm = "ensemble_model/version_5/arima_2021_2023.rds",
path_lhm = "ensemble_model/version_5/holiday_effect_2021_2023.rds",
from_month = 1,
to_month = 1,
raw_fc_ensembled = raw_fc_ensembled)
คะแนนที่มั่นคงของ MAPE 3.8% สำหรับ version_5 (รุ่น LHM + DHR)
เรามาดูรายละเอียดกันดีกว่าว่าเราจะใช้เฉพาะโมเดล ARIMA (arima_14) หรือไม่ รูปที่ 14 แสดงถึงผลลัพธ์สำหรับรุ่นนี้ เราจะเห็นวันหยุด (สีส้ม) วันหยุดสุดสัปดาห์ (สีแดง) และวันธรรมดา (สีน้ำเงิน) มีค่าผิดปกติที่สำคัญสำหรับวันหยุด แม้ว่าจะมีตัวแปรจำลองสำหรับโมเดล ARIMA แต่ก็ไม่สามารถตรวจจับวันหยุดได้อย่างถูกต้อง
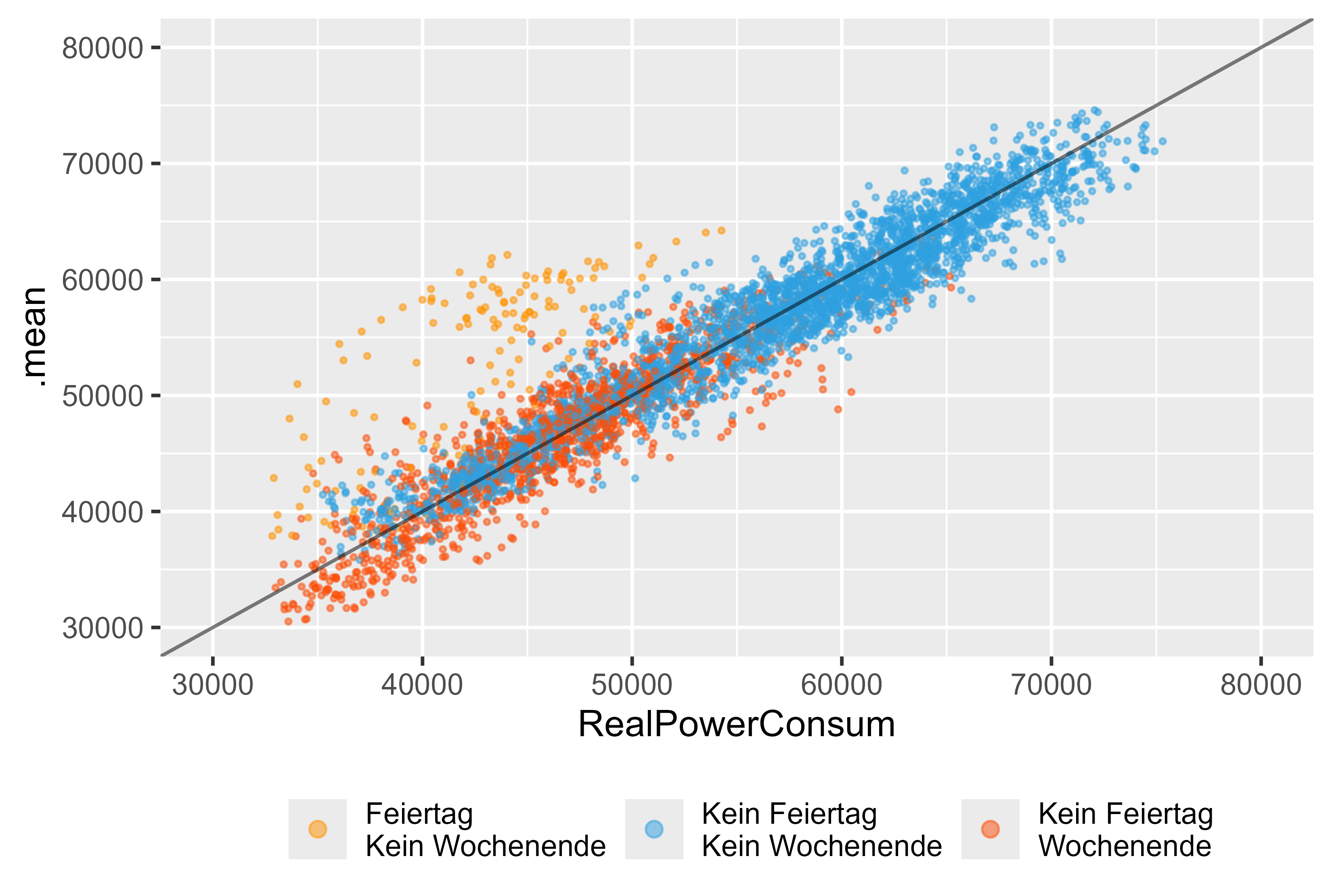รูปที่ 14 การคาดการณ์เทียบกับมูลค่าจริง ARIMA (DHR, arima_14) ในรูปแบบเดียว
ในทางกลับกัน โมเดล LHM + DHR แสดงให้เห็นประสิทธิภาพที่ดีขึ้นในช่วงวันหยุด รูปที่ 15 แสดงถึงมัน
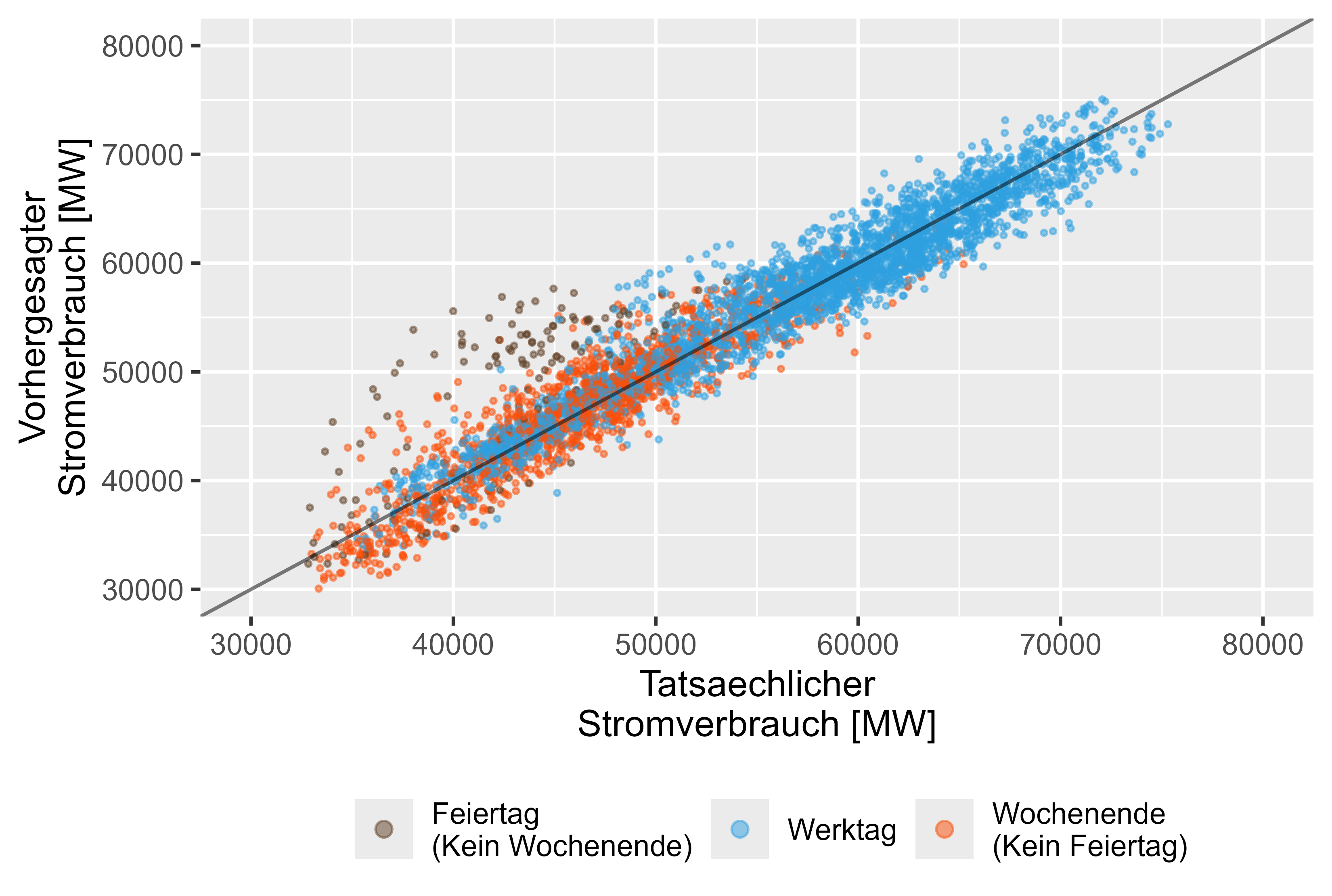รูปที่ 15 การคาดการณ์เทียบกับมูลค่าจริง LHM + DHR แบบจำลองทั้งมวล
รูปที่ 16 แสดงการคาดการณ์เดือนมกราคม 2567 ถือว่าสมเหตุสมผล
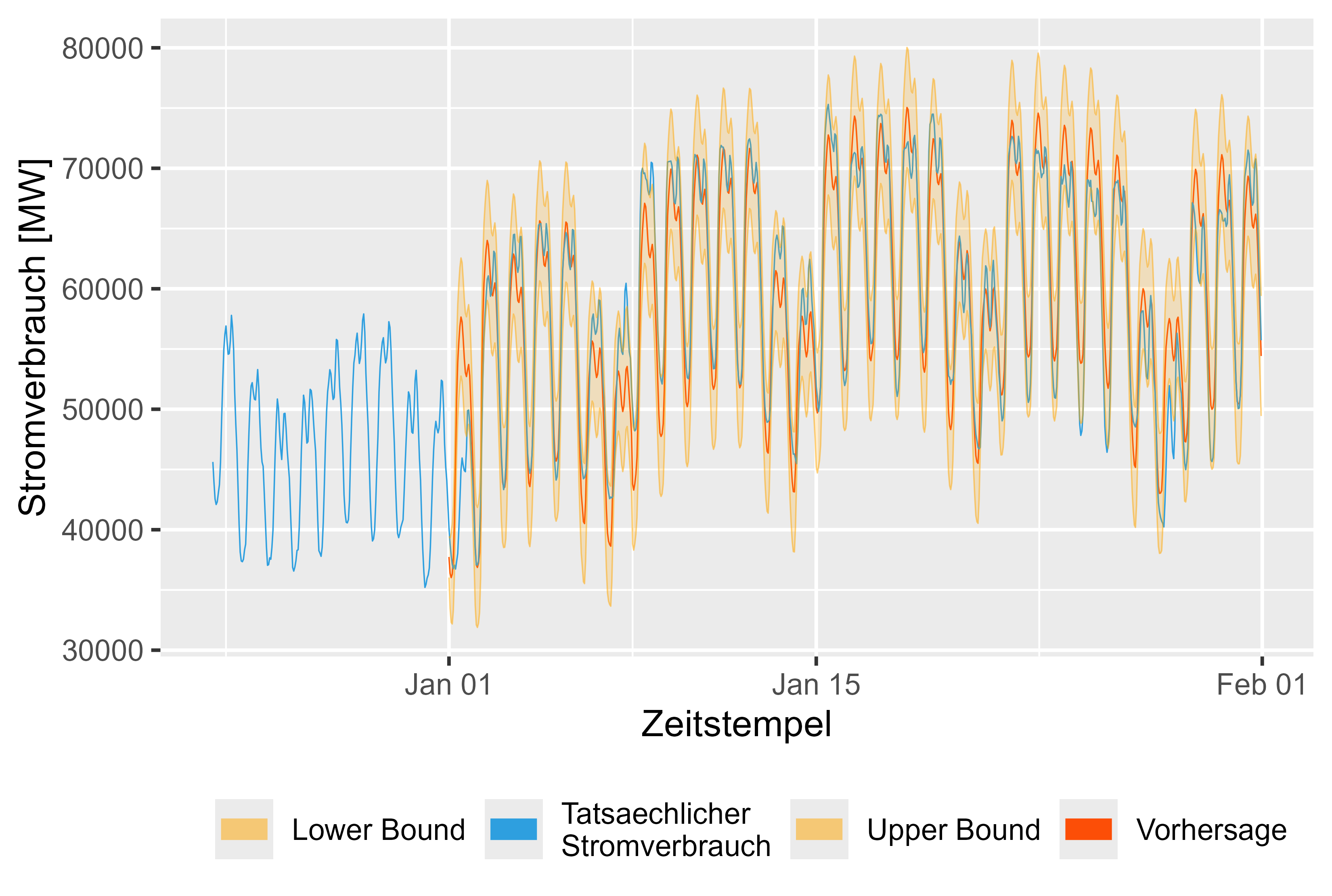รูปที่ 16 การคาดการณ์เทียบกับมูลค่าจริง LHM + DHR สำหรับเดือนมกราคม 2567
นอกจากนี้ส่วนที่เหลือของโมเดลเมื่อเปรียบเทียบกับรุ่น SMARD ก็ดูดีเช่นกัน มีจุดเพิ่มขึ้นเล็กน้อยซึ่งอาจมีนัยสำคัญและอาจเตรียมการได้ดีขึ้นโดยการสร้างแบบจำลอง แต่โดยรวมแล้วได้ผลที่มั่นคง
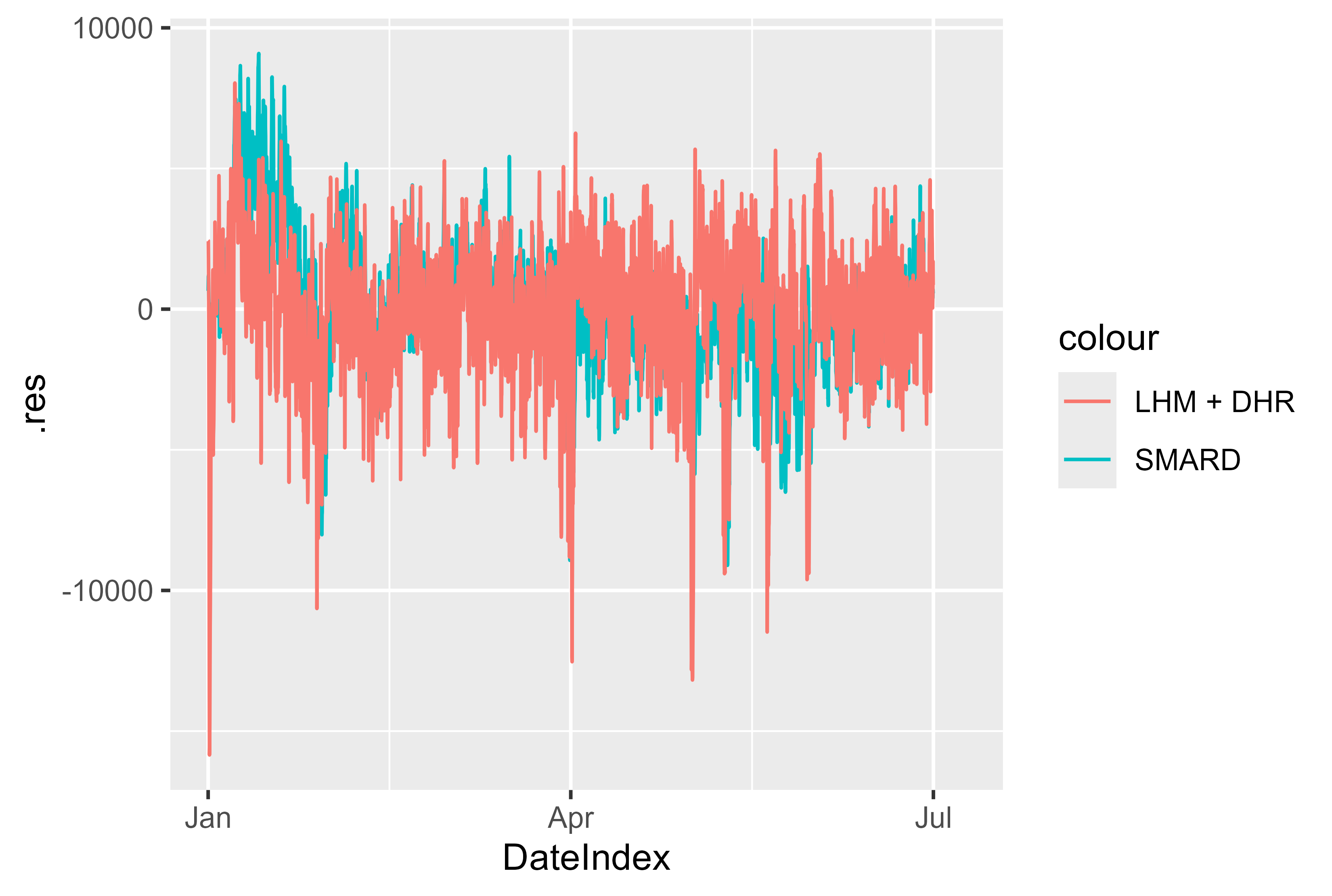ภาพที่ 17 ปริมาณคงเหลือ LHM + DHR เดือนมกราคม-กรกฎาคม 2567
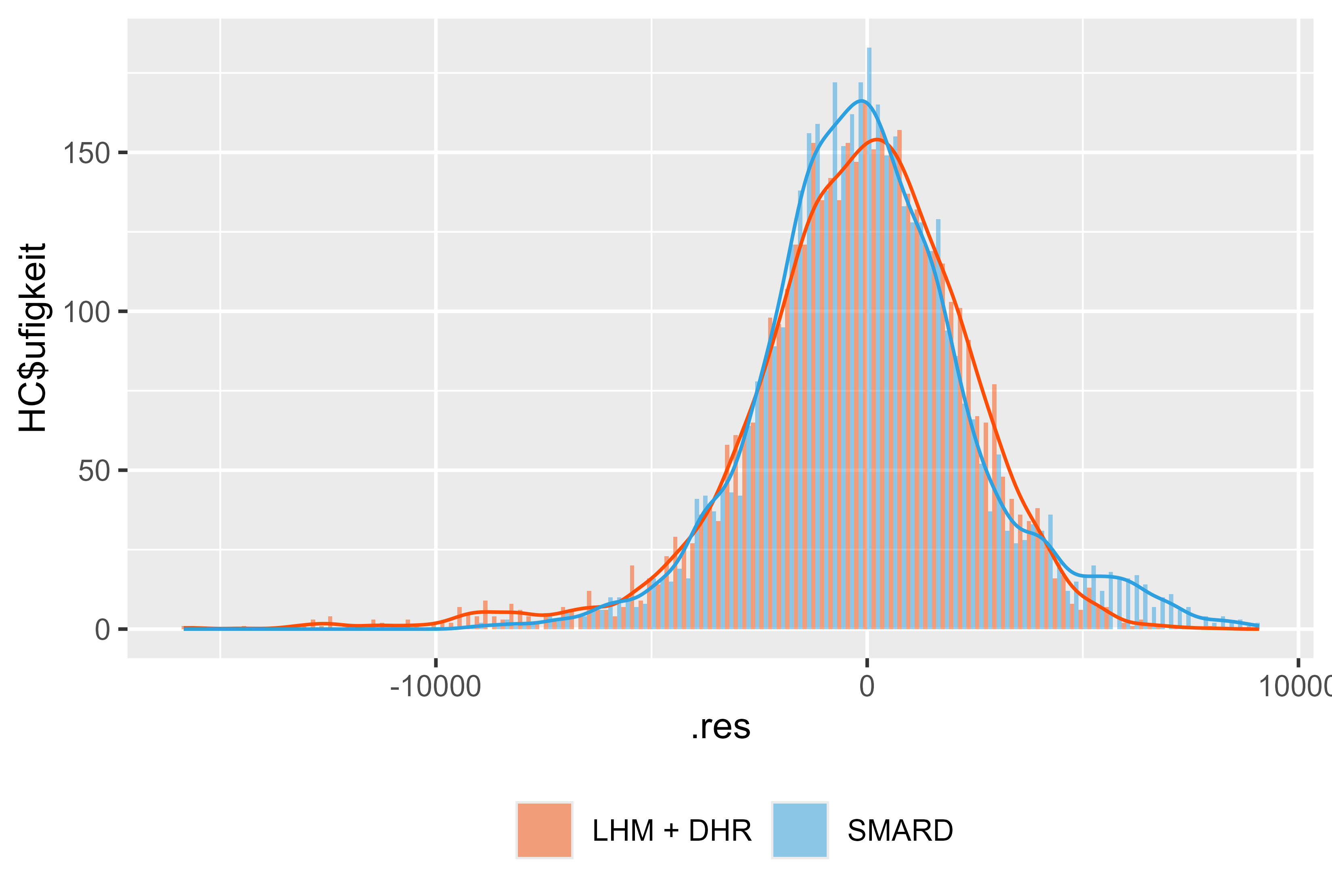ภาพที่ 18 ปริมาณคงเหลือ LHM + DHR เดือนมกราคม-กรกฎาคม 2567
| ดัชนี | ชื่อรุ่น | RMSE | เมเป | แม่ | ประกอบ |
|---|---|---|---|---|---|
| 2 | ข้อสังเกตที่แท้จริง | 0.000 | 0.000000 | 0.000 | จริง |
| 3 | สมาร์ท | 2480.693 | 3.602140 | 1869.466 | เท็จ |
| 4 | สมาร์ท | 2480.693 | 3.602140 | 1869.466 | จริง |
| 5 | รุ่น_5 | 2626.807 | 3.816012 | 1937.670 | จริง |
| 6 | รุ่น_0 | 2613.258 | 3.846888 | 1946.314 | จริง |
| 7 | รุ่น_7 | 2770.359 | 4.107272 | 2076.045 | จริง |
| 8 | รุ่น_8 | 2775.441 | 4.146788 | 2091.153 | จริง |
| 9 | รุ่น_9 | 2887.179 | 4.177841 | 2100.381 | จริง |
| 10 | รุ่น_6 | 2906.242 | 4.216517 | 2142.092 | จริง |
| 11 | arima_14_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | เท็จ |
| 12 | arima_18_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | เท็จ |
| 13 | รุ่น_4 | 2875.929 | 4.535388 | 2255.645 | จริง |
| 14 | รุ่น_2 | 2905.990 | 4.580770 | 2279.624 | จริง |
| 15 | arima_9_2021_2023.rds | 3267.160 | 4.611857 | 2302.918 | เท็จ |
| 16 | arima_2_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | เท็จ |
| 17 | arima_4_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | เท็จ |
| 18 | arima_5_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | เท็จ |
| 19 | arima_13_2021_2023.rds | 3283.745 | 4.619636 | 2307.415 | เท็จ |
| 20 | arima_10_2021_2023.rds | 3265.913 | 4.625508 | 2314.395 | เท็จ |
| 21 | arima_0_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | เท็จ |
| 22 | arima_17_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | เท็จ |
| 23 | arima_16_2021_2023.rds | 3298.902 | 4.673116 | 2334.857 | เท็จ |
| 24 | arima_1_2021_2023.rds | 3312.429 | 4.696342 | 2340.193 | เท็จ |
| 24 | ศาสดา_0_2021_2023.rds | 3044.849 | 4.711527 | 2435.572 | เท็จ |
| 25 | arima_8_2021_2023.rds | 3332.217 | 4.716612 | 2358.085 | เท็จ |
| 26 | arima_11_2021_2023.rds | 3358.020 | 4.758970 | 2388.791 | เท็จ |
| 27 | arima_12_2021_2023.rds | 3430.191 | 5.022772 | 2495.067 | เท็จ |
| 28 | arima_7_2021_2023.rds | 3475.671 | 5.049287 | 2510.903 | เท็จ |
| 29 | รุ่น_3 | 3546.729 | 5.064654 | 2570.530 | จริง |
| 30 | arima_15_2021_2023.rds | 3734.584 | 5.165147 | 2606.661 | เท็จ |
| 31 | arima_6_2021_2023.rds | 3748.583 | 5.375326 | 2723.837 | เท็จ |
| 32 | รุ่น_1 | 4495.568 | 6.483477 | 3229.647 | จริง |
| 33 | arima_3_2021_2023.rds | 4558.982 | 6.953247 | 3453.387 | เท็จ |
| 34 | tslm_0_2021_2023.rds | 6760.994 | 11.189119 | 5694.949 | เท็จ |
| 35 | Mean_2021_2023.rds | 9489.303 | 16.406032 | 8101.476 | เท็จ |
| 36 | naive_2021_2023.rds | 14699.338 | 20.797370 | 12130.587 | เท็จ |
| 37 | drift_2021_2023.rds | 14763.692 | 20.917883 | 12200.002 | เท็จ |
บันทึก:
ตรวจสอบตัวอย่าง/ensemble_model_2022_forecast หรือตัวอย่าง/ensemble_model_2023_forecast
เราอาจรวมปัจจัยเพิ่มเติม เช่น:
