แก้ปริศนาหอคอยแห่งฮานอยด้วยการเรียนรู้แบบเสริมกำลัง
ในสภาพแวดล้อม Python ที่ติดตั้ง Numpy และ Pandas ให้รันสคริปต์ hanoi.py เพื่อสร้างสามแปลงที่แสดงในส่วนผลลัพธ์ สคริปต์สามารถปรับให้เข้ากับการเล่นเกมโดยใช้ดิสก์จำนวนที่แตกต่างกัน N ได้อย่างง่ายดาย
เมื่อเร็วๆ นี้การเรียนรู้แบบเสริมกำลังได้รับความสนใจอีกครั้งด้วยการเอาชนะ AlphaGo ของ Google Deepmind ซึ่งเป็นผู้เล่น Go มืออาชีพ ที่นี่ไขปริศนาที่ง่ายกว่า: เกม Tower of Hanoi การนำไปปฏิบัติเป็นไปตามอัลกอริธึม Q-learning ตามที่เสนอโดย Watkins & Dayan [1]
เกมหอคอยแห่งฮานอยประกอบด้วยหมุดสามอันและดิสก์หลายขนาดหลายขนาดซึ่งสามารถเลื่อนไปบนหมุดได้ ปริศนาเริ่มต้นด้วยดิสก์ทั้งหมดเรียงซ้อนกันบนหมุดแรกตามลำดับจากน้อยไปหามาก โดยดิสก์ที่ใหญ่ที่สุดอยู่ด้านล่างและเล็กที่สุดอยู่ด้านบน วัตถุประสงค์ของเกมคือการย้ายดิสก์ทั้งหมดไปยังหมุดที่สาม การย้ายที่ถูกต้องตามกฎหมายเพียงอย่างเดียวคือการย้ายดิสก์บนสุดจากหมุดหนึ่งไปยังอีกหมุดหนึ่ง โดยมีข้อจำกัดว่าห้ามวางดิสก์บนดิสก์ที่มีขนาดเล็กกว่า รูปที่ 1 แสดงวิธีแก้ปัญหาที่ดีที่สุดสำหรับดิสก์ 4 แผ่น

รูปที่ 1 โซลูชั่นภาพเคลื่อนไหวของปริศนา Tower of Hanoi สำหรับ 4 ดิสก์ (ที่มา: วิกิพีเดีย)
หลังจาก Anderson [2] เรานำเสนอสถานะของเกมด้วยสิ่งอันดับ โดยที่องค์ประกอบที่ i ระบุว่าหมุดใดที่ดิสก์ที่ i เปิดอยู่ ดิสก์จะมีป้ายกำกับตามขนาดที่เพิ่มขึ้น ดังนั้นสถานะเริ่มต้นคือ (111) และสถานะสุดท้ายที่ต้องการคือ (333) (รูปที่ 2)
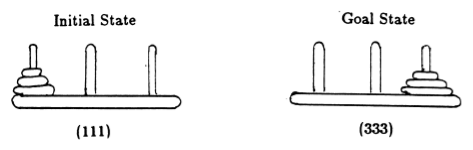
รูปที่ 2 สถานะเริ่มต้นและเป้าหมายของปริศนาหอคอยฮานอยพร้อมดิสก์ 3 แผ่น (จาก [2])
สถานะของปริศนาและการเปลี่ยนระหว่างสถานะเหล่านั้นซึ่งสอดคล้องกับการเคลื่อนไหวทางกฎหมายจะสร้างกราฟการเปลี่ยนสถานะของปริศนา ซึ่งแสดงในรูปที่ 3
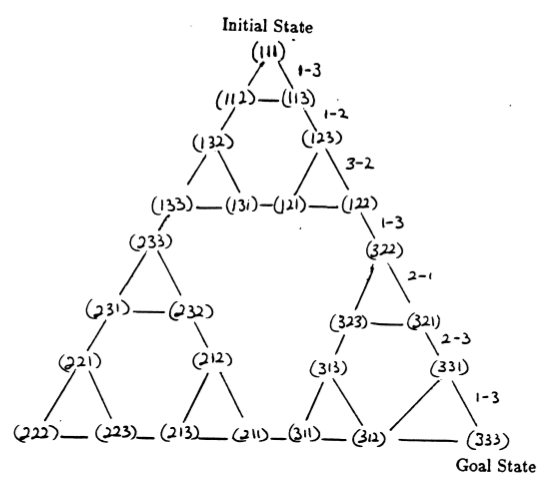
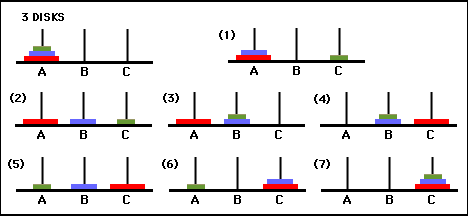
รูปที่ 3 กราฟการเปลี่ยนแปลงสถานะสำหรับปริศนาหอคอยฮานอยสามดิสก์ (ด้านบน) และวิธีแก้ปัญหา 7 การเคลื่อนไหวที่เหมาะสมที่สุด (ด้านล่าง) ซึ่งเป็นไปตามเส้นทางทางด้านขวามือของกราฟ (จาก [2] และ Mathforum.org)
จำนวนการเคลื่อนไหวขั้นต่ำที่จำเป็นในการไขปริศนาหอคอยแห่งฮานอยคือ 2 N - 1 โดยที่ N คือจำนวนดิสก์ ดังนั้นสำหรับ N = 3 ปริศนาสามารถแก้ไขได้ใน 7 การเคลื่อนไหว ดังแสดงในรูปที่ 3 ในส่วนต่อไปนี้ เราจะสรุปว่า Q-learning บรรลุผลสำเร็จได้อย่างไร
R และเมทริกซ์ 'มูลค่าการกระทำ' Q สำหรับ 2 ดิสก์ ขั้นตอนแรกในโปรแกรมคือการสร้าง เมทริกซ์รางวัล R ซึ่งรวบรวมกฎของเกมและให้รางวัลสำหรับการชนะ เพื่อความง่าย เมทริกซ์รางวัลจะแสดงสำหรับดิสก์ N = 2 ในรูปที่ 4
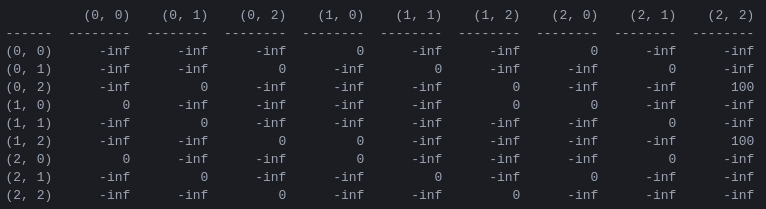
รูปที่ 4 รางวัลเมทริกซ์ R สำหรับปริศนาหอคอยฮานอยที่มีดิสก์ N = 2 แผ่น องค์ประกอบที่ ( i , j ) แสดงถึงรางวัลสำหรับการย้ายจากสถานะ i ไป j สถานะจะถูกติดป้ายกำกับด้วยสิ่งอันดับดังในรูปที่ 2 และ 3 โดยมีความแตกต่างที่หมุดถูกจัดทำดัชนี 'pythonically' จาก 0 ถึง 2 แทนที่จะเป็นจาก 1 ถึง 3 การเคลื่อนไหวที่นำไปสู่สถานะเป้าหมาย (2,2) จะได้รับรางวัล ของ 100 การเคลื่อนไหวที่ผิดกฎหมายของ และการเคลื่อนไหวอื่นๆ ทั้งหมดของ 0
เมทริกซ์รางวัล R อธิบายเฉพาะรางวัล ทันที เท่านั้น รางวัล 100 สามารถทำได้จากสถานะสุดท้าย (0,2) และ (1,2) เท่านั้น ในรัฐอื่นๆ แต่ละการเคลื่อนไหวที่เป็นไปได้ 2 หรือ 3 ครั้งจะได้รับรางวัลเท่ากับ 0 และไม่มีเหตุผลที่ชัดเจนในการเลือกอย่างใดอย่างหนึ่ง
ท้ายที่สุดแล้ว เราพยายามที่จะกำหนด 'คุณค่า' ให้กับการเคลื่อนไหวที่เป็นไปได้ในแต่ละรัฐ เพื่อที่ว่าด้วยการเพิ่มค่าเหล่านี้ให้สูงสุด เราจะสามารถกำหนด นโยบาย ที่นำไปสู่ทางออกที่ดีที่สุดได้ เมทริกซ์ของ 'ค่า' สำหรับแต่ละการกระทำในแต่ละสถานะเรียกว่า Q และสามารถแก้แบบวนซ้ำหรือ 'เรียนรู้' ในลักษณะสุ่มตามที่อธิบายโดย Watkins และ Dayan [1] ผลลัพธ์สำหรับดิสก์ 2 แผ่นแสดงในรูปที่ 5
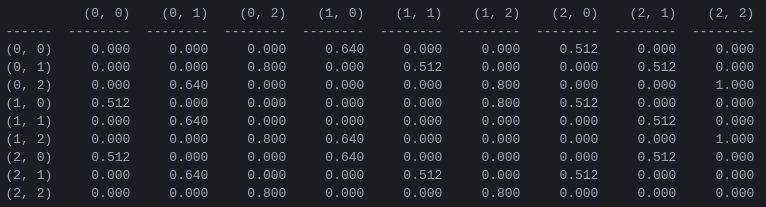
รูปที่ 5 เมทริกซ์ 'มูลค่าการดำเนินการ' Q สำหรับเกม Tower of Hanoi ที่มีดิสก์ 2 แผ่น เรียนรู้ด้วยปัจจัยลด = 0.8 ปัจจัยการเรียนรู้ = 1.0 และตอนการฝึกอบรม 1,000 ตอน
ค่าของเมทริกซ์ Q คือน้ำหนักโดยพื้นฐานแล้ว ซึ่งสามารถกำหนดให้กับจุดยอดของกราฟการเปลี่ยนสถานะในรูปที่ 3 ซึ่งนำทางเอเจนต์จากสถานะเริ่มต้นไปยังสถานะเป้าหมายด้วยวิธีที่สั้นที่สุดเท่าที่จะเป็นไปได้ ในตัวอย่างนี้ โดยการเริ่มต้นที่สถานะ (0,0) และเลือกการเคลื่อนไหวที่มีค่าสูงสุดของ Q อย่างต่อเนื่อง ผู้อ่านสามารถโน้มน้าวตัวเองว่าเมทริกซ์ Q นำเอเจนต์ผ่านลำดับของสถานะ (0,0) - (1 ,0) - (1,2) - (2,2) ซึ่งสอดคล้องกับแนวทางการแก้ปัญหาที่เหมาะสมที่สุด 3 จังหวะของเกม Tower of Hanoi 2 ดิสก์ (รูปที่ 6)
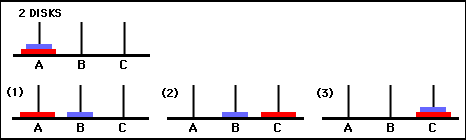
รูปที่ 6 วิธีแก้ปัญหาเกม Tower of Hanoi พร้อมดิสก์ 2 แผ่น สถานะที่ต่อเนื่องกันจะแสดงด้วย (0,0), (1,0), (1,2) และ (2,2) ตามลำดับ (ที่มา: mathforum.org)
ในตัวอย่างนี้ เมื่อเมทริกซ์ Q ได้บรรจบกันเป็นค่าที่เหมาะสมที่สุด จะกำหนดนโยบาย คงที่ : แต่ละแถวมีการดำเนินการหนึ่งรายการโดยมีค่าสูงสุดที่ไม่ซ้ำกัน อย่างไรก็ตาม ในระหว่างกระบวนการเรียนรู้ การกระทำที่แตกต่างกันอาจมีค่า Q เท่ากัน (โดยเฉพาะอย่างยิ่ง นี่เป็นกรณีเมื่อเริ่มต้นการฝึกเมื่อ Q เริ่มต้นเป็นเมทริกซ์ที่เป็นศูนย์) ในการจำลองที่นำเสนอในส่วนต่อไปนี้ สถานการณ์ดังกล่าวได้รับการจัดการโดยนโยบาย สุ่ม ต่อไปนี้: ในกรณีที่ค่า Q สูงสุดถูกใช้ร่วมกันในหลายการกระทำ ให้เลือกการกระทำอย่างใดอย่างหนึ่งเหล่านี้โดยการสุ่ม
ประสิทธิภาพของอัลกอริธึม Q-learning สามารถวัดได้โดยการนับจำนวนการเคลื่อนไหวที่ใช้ (โดยเฉลี่ย) เพื่อไขปริศนาหอคอยแห่งฮานอย จำนวนนี้จะลดลงตามจำนวนตอนการฝึกจนกว่าจะถึงค่าที่เหมาะสมที่สุด 2 N - 1 โดยที่ N คือจำนวนดิสก์ ดังแสดงในรูปที่ 7 สำหรับ N = 2, 3 และ 4
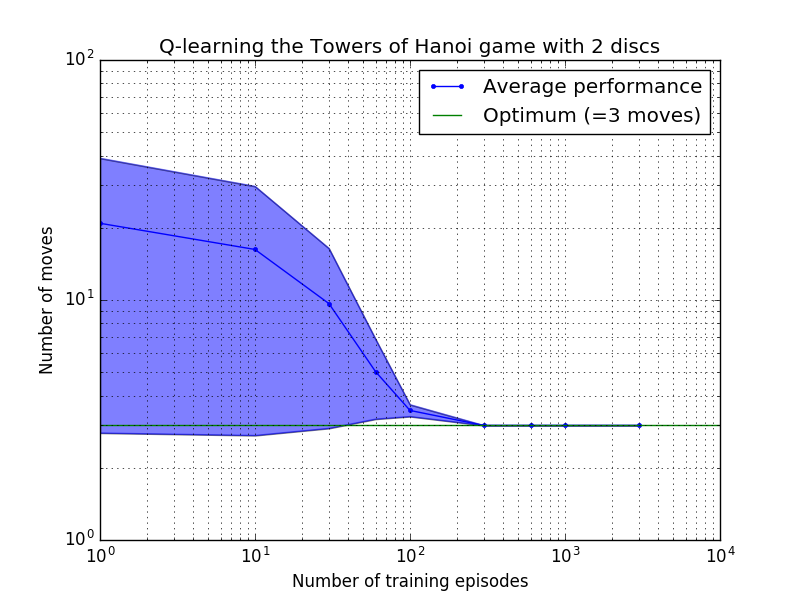
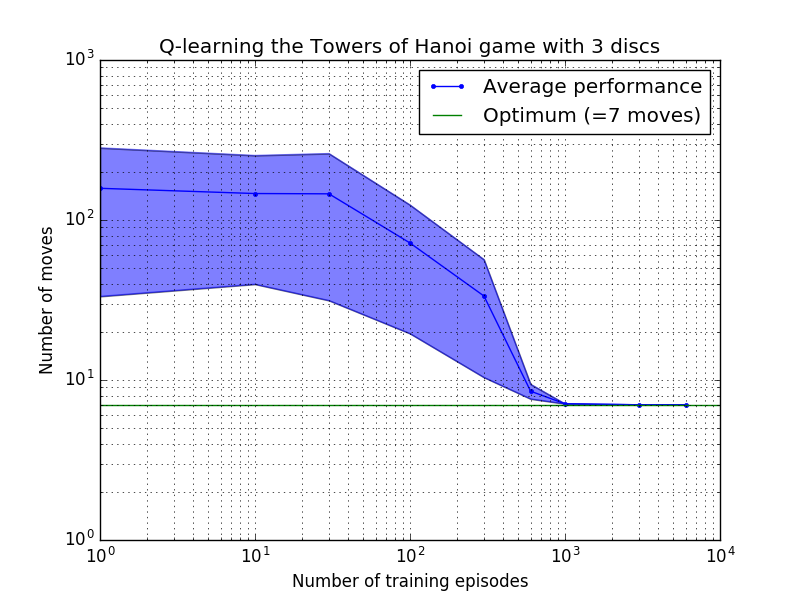
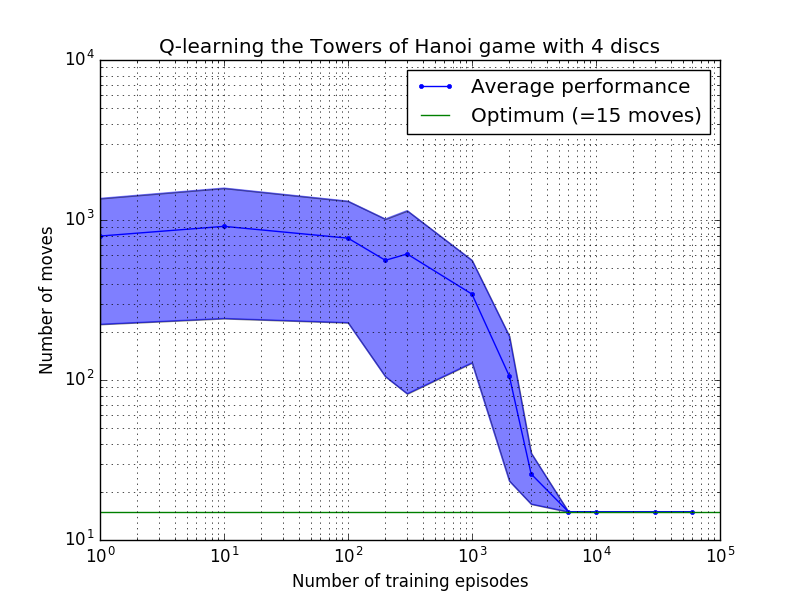
รูปที่ 7 ประสิทธิภาพของอัลกอริธึม Q-learning สำหรับเกม Tower of Hanoi ที่มีดิสก์ 2, 3 และ 4 แผ่นจากบนลงล่าง ในทุกกรณี การเรียนรู้ดำเนินการโดยมีปัจจัยคิดลด = 0.8 และปัจจัยการเรียนรู้ = 1.0 เส้นโค้งสีน้ำเงินทึบแสดงถึงประสิทธิภาพโดยเฉลี่ยในช่วง 100 ยุคของการฝึกซ้อมและการเล่นเกม 100 ครั้งสำหรับแต่ละนโยบายสุ่มผลลัพธ์ ขอบเขตบนและล่างของพื้นที่สีน้ำเงินที่แรเงาจะหักล้างจากค่าเฉลี่ยด้วยค่าเบี่ยงเบนมาตรฐานโดยประมาณ (สำหรับ N = 3 และ N = 4 จำนวนตอนการฝึกอบรมและเวลาในการเล่นลดลงเหลือ 10 และ 10 ตามลำดับ เนื่องจากข้อจำกัดในการคำนวณ)
คุณลักษณะที่น่าสนใจของคุณลักษณะการเรียนรู้ในรูปที่ 7 คือ ในทุกกรณี การเรียนรู้จะช้าในช่วงแรก และตัวแทนแทบจะไม่ทำได้ดีไปกว่านโยบาย 'การฝึกอบรมแบบศูนย์' ในการเลือกการเคลื่อนไหวโดยการสุ่ม เมื่อถึงจุดหนึ่ง การเรียนรู้จะไปถึง 'จุดเปลี่ยน' จากนั้นจึงมาบรรจบกันเป็นจำนวนการเคลื่อนไหวที่เหมาะสมที่สุดด้วยความเร่ง (แม้ว่าระดับลอการิทึมจะเกินจริงไปบ้างก็ตาม)
สคริปต์ Python ประสบความสำเร็จในการไขปริศนา Tower of Hanoi ได้อย่างเหมาะสมที่สุดสำหรับดิสก์จำนวนเท่าใดก็ได้โดย Q-learning สคริปต์สามารถปรับให้เข้ากับปัญหาอื่นๆ ได้อย่างง่ายดายด้วยเมทริกซ์รางวัล R ที่แตกต่างกัน
จำนวนตอนการฝึกอบรมที่จำเป็นในการรวมกันเป็นโซลูชันที่ดีที่สุดจะเพิ่มขึ้นอย่างมากตามจำนวนดิสก์ N : สำหรับดิสก์ N=2 จะใช้เวลา ~300 ตอน ในขณะที่สำหรับ N=4 จะใช้เวลา ~6,000 การปรับปรุงที่เป็นไปได้ของอัลกอริธึมการเรียนรู้คือการอนุญาตให้ค้นหาวิธีแก้ปัญหาแบบเรียกซ้ำโดยอัตโนมัติ ดังที่ทำโดย Hengst [3]
[ 1 ] Watkins & Dayan, Q-learning , การเรียนรู้ของเครื่อง, 8, 279-292 (1992) (ไฟล์ PDF)
[ 2 ] แอนเดอร์สัน การเรียนรู้และการแก้ปัญหาด้วยระบบการเชื่อมต่อหลายชั้น ปริญญาเอก วิทยานิพนธ์ (2529) (ไฟล์ PDF)
[ 3 ] Hengst, การค้นพบลำดับชั้นในการเรียนรู้แบบเสริมแรงด้วย HEXQ , การดำเนินการในการประชุมนานาชาติเรื่อง Machine Learning ครั้งที่ 19 (2002) (ไฟล์ PDF)