nano neuron

นาโนนิวรอน

7 ฟังก์ชั่น JavaScript ง่ายๆ ที่จะทำให้คุณรู้สึกว่าเครื่องจักรสามารถ "เรียนรู้" ได้อย่างไร

ในภาษาอื่น: Русский, Português

คุณอาจจะสนใจ ? การทดลองการเรียนรู้ของเครื่องเชิงโต้ตอบ

TL;ดร

NanoNeuron เป็นแนวคิด Neuron เวอร์ชัน ที่เรียบง่ายเกินไป จาก Neural Networks NanoNeuron ได้รับการฝึกฝนให้แปลงค่าอุณหภูมิจากเซลเซียสเป็นฟาเรนไฮต์

ตัวอย่างโค้ด NanoNeuron.js มีฟังก์ชัน JavaScript ง่ายๆ 7 รายการ (ซึ่งเกี่ยวข้องกับการคาดการณ์แบบจำลอง การคำนวณต้นทุน การแพร่กระจายไปข้างหน้า/ข้างหลัง และการฝึกอบรม) ซึ่งจะทำให้คุณรู้สึกว่าเครื่องจักรสามารถ "เรียนรู้" ได้อย่างไร ไม่มีไลบรารีของบุคคลที่สาม ไม่มีชุดข้อมูลภายนอกหรือการอ้างอิง มีเพียงฟังก์ชัน JavaScript ล้วนๆ และเรียบง่ายเท่านั้น

? ฟังก์ชั่นเหล่านี้ ไม่ใช่ คำแนะนำที่สมบูรณ์สำหรับการเรียนรู้ของเครื่อง แนวคิดการเรียนรู้ของเครื่องจำนวนมากถูกข้ามและทำให้ง่ายเกินไป! การลดความซับซ้อนนี้มีวัตถุประสงค์เพื่อให้ผู้อ่านมีความเข้าใจ พื้นฐาน และความรู้สึกว่าเครื่องจักรสามารถเรียนรู้ได้อย่างไร และท้ายที่สุดก็ทำให้ผู้อ่านรับรู้ว่าไม่ใช่ "การเรียนรู้ของเครื่อง MAGIC" แต่เป็น "คณิตศาสตร์การเรียนรู้ของเครื่อง" หรือไม่

สิ่งที่ NanoNeuron ของเราจะได้เรียนรู้

คุณคงเคยได้ยินเกี่ยวกับเซลล์ประสาทในบริบทของโครงข่ายประสาทเทียม NanoNeuron นั้นเรียบง่ายกว่า และเราจะนำไปใช้ตั้งแต่ต้น ด้วยเหตุผลที่เรียบง่าย เราจะไม่สร้างเครือข่ายบน NanoNeurons ด้วยซ้ำ เราจะทำให้มันทั้งหมดทำงานด้วยตัวมันเอง และทำการทำนายที่มหัศจรรย์ให้กับเรา กล่าวคือ เราจะสอน NanoNeuron เอกพจน์นี้ให้แปลง (ทำนาย) อุณหภูมิจากเซลเซียสเป็นฟาเรนไฮต์

อย่างไรก็ตาม สูตรในการแปลงเซลเซียสเป็นฟาเรนไฮต์คือ:

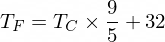
แต่ตอนนี้ NanoNeuron ของเรายังไม่รู้เรื่องนี้...

โมเดลนาโนนิวรอน

ลองใช้ฟังก์ชันแบบจำลอง NanoNeuron ของเรา มันใช้การพึ่งพาเชิงเส้นพื้นฐานระหว่าง x และ y ซึ่งดูเหมือน y = w * x + b เพียงแค่บอกว่า NanoNeuron ของเราเป็น "เด็ก" ใน "โรงเรียน" ที่ถูกสอนให้วาดเส้นตรงในพิกัด XY

ตัวแปร w ​​, b คือพารามิเตอร์ของโมเดล NanoNeuron รู้เพียงพารามิเตอร์สองตัวนี้ของฟังก์ชันเชิงเส้นเท่านั้น พารามิเตอร์เหล่านี้เป็นสิ่งที่ NanoNeuron จะ "เรียนรู้" ในระหว่างกระบวนการฝึกอบรม

สิ่งเดียวที่ NanoNeuron ทำได้คือเลียนแบบการพึ่งพาเชิงเส้น ในวิธี predict() จะยอมรับอินพุต x และทำนายเอาต์พุต y ไม่มีเวทย์มนตร์ที่นี่

 function NanoNeuron ( w , b ) {
  this . w = w ;
  this . b = b ;
  this . predict = ( x ) => {
    return x * this . w + this . b ;
  }
}

(...เดี๋ยวก่อน... การถดถอยเชิงเส้นใช่คุณหรือเปล่า?) ?

การแปลงเซลเซียสเป็นฟาเรนไฮต์

ค่าอุณหภูมิในหน่วยเซลเซียสสามารถแปลงเป็นฟาเรนไฮต์ได้โดยใช้สูตรต่อไปนี้: f = 1.8 * c + 32 โดยที่ c คืออุณหภูมิในหน่วยเซลเซียส และ f คืออุณหภูมิที่คำนวณได้ในหน่วยฟาเรนไฮต์

 function celsiusToFahrenheit ( c ) {
  const w = 1.8 ;
  const b = 32 ;
  const f = c * w + b ;
  return f ;
} ;

ท้ายที่สุดแล้ว เราต้องการสอน NanoNeuron ให้เลียนแบบฟังก์ชันนี้ (เพื่อเรียนรู้ว่า w = 1.8 และ b = 32 ) โดยไม่ทราบพารามิเตอร์เหล่านี้ล่วงหน้า

นี่คือลักษณะของฟังก์ชันการแปลงเซลเซียสเป็นฟาเรนไฮต์:

การสร้างชุดข้อมูล

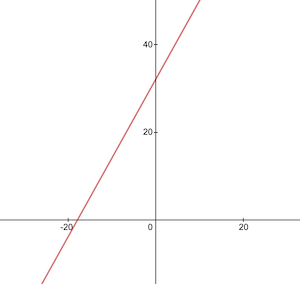
ก่อนการฝึกอบรม เราจำเป็นต้องสร้าง ชุดข้อมูล การฝึกอบรม และทดสอบตามฟังก์ชัน celsiusToFahrenheit() ชุดข้อมูลประกอบด้วยคู่ของค่าอินพุตและค่าเอาต์พุตที่มีป้ายกำกับอย่างถูกต้อง

ในชีวิตจริง ในกรณีส่วนใหญ่ ข้อมูลนี้จะถูกรวบรวมแทนที่จะสร้างขึ้น ตัวอย่างเช่น เราอาจมีชุดรูปภาพตัวเลขที่วาดด้วยมือและชุดตัวเลขที่สอดคล้องกันซึ่งอธิบายว่าแต่ละภาพเขียนตัวเลขอะไร

เราจะใช้ข้อมูลตัวอย่างการฝึกอบรมเพื่อฝึก NanoNeuron ของเรา ก่อนที่ NanoNeuron ของเราจะเติบโตและสามารถตัดสินใจได้ด้วยตัวเอง เราต้องสอนมันว่าอะไรถูกและสิ่งผิดโดยใช้ตัวอย่างการฝึกอบรม

เราจะใช้ตัวอย่าง TEST เพื่อประเมินว่า NanoNeuron ของเราทำงานได้ดีเพียงใดกับข้อมูลที่ไม่ได้เห็นระหว่างการฝึก นี่คือจุดที่เราเห็นได้ว่า "ลูก" ของเราเติบโตขึ้นและสามารถตัดสินใจได้ด้วยตัวเอง

 function generateDataSets ( ) {
  // xTrain -> [0, 1, 2, ...],
  // yTrain -> [32, 33.8, 35.6, ...]
  const xTrain = [ ] ;
  const yTrain = [ ] ;
  for ( let x = 0 ; x < 100 ; x += 1 ) {
    const y = celsiusToFahrenheit ( x ) ;
    xTrain . push ( x ) ;
    yTrain . push ( y ) ;
  }

  // xTest -> [0.5, 1.5, 2.5, ...]
  // yTest -> [32.9, 34.7, 36.5, ...]
  const xTest = [ ] ;
  const yTest = [ ] ;
  // By starting from 0.5 and using the same step of 1 as we have used for training set
  // we make sure that test set has different data comparing to training set.
  for ( let x = 0.5 ; x < 100 ; x += 1 ) {
    const y = celsiusToFahrenheit ( x ) ;
    xTest . push ( x ) ;
    yTest . push ( y ) ;
  }

  return [ xTrain , yTrain , xTest , yTest ] ;
}

ต้นทุน (ข้อผิดพลาด) ของการทำนาย

เราจำเป็นต้องมีตัวชี้วัดที่จะแสดงให้เห็นว่าการคาดการณ์ของแบบจำลองของเราใกล้เคียงแค่ไหนในการแก้ไขค่า การคำนวณต้นทุน (ข้อผิดพลาด) ระหว่างค่าเอาต์พุตที่ถูกต้องของ y และ prediction ที่ NanoNeuron ของเราสร้างขึ้น จะดำเนินการโดยใช้สูตรต่อไปนี้:

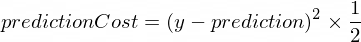
นี่เป็นข้อแตกต่างง่ายๆ ระหว่างสองค่า ยิ่งค่าอยู่ใกล้กัน ความแตกต่างก็จะน้อยลง เราใช้กำลัง 2 ตรงนี้เพื่อกำจัดจำนวนลบ เพื่อว่า (1 - 2) ^ 2 จะเหมือนกับ (2 - 1) ^ 2 การหารด้วย 2 เกิดขึ้นเพียงเพื่อทำให้สูตรการขยายพันธุ์แบบย้อนกลับง่ายขึ้น (ดูด้านล่าง)

ฟังก์ชันต้นทุนในกรณีนี้จะง่ายเพียง:

 function predictionCost ( y , prediction ) {
  return ( y - prediction ) ** 2 / 2 ; // i.e. -> 235.6
}

การขยายพันธุ์ไปข้างหน้า

การเผยแพร่ไปข้างหน้าหมายถึงการคาดการณ์สำหรับตัวอย่างการฝึกอบรมทั้งหมดจากชุดข้อมูล xTrain และ yTrain และคำนวณต้นทุนเฉลี่ยของการคาดการณ์เหล่านั้นไปพร้อมกัน

ณ จุดนี้ เราเพียงปล่อยให้ NanoNeuron ของเราแสดงความคิดเห็น โดยปล่อยให้มันเดาว่าจะแปลงอุณหภูมิอย่างไร มันอาจจะผิดอย่างโง่เขลาที่นี่ ต้นทุนเฉลี่ยจะแสดงให้เราเห็นว่าโมเดลของเราผิดพลาดอย่างไรในขณะนี้ มูลค่าต้นทุนนี้มีความสำคัญมากตั้งแต่เปลี่ยนพารามิเตอร์ NanoNeuron w และ b และโดยทำการเผยแพร่ไปข้างหน้าอีกครั้ง เราจะสามารถประเมินได้ว่า NanoNeuron ของเราฉลาดขึ้นหรือไม่หลังจากการเปลี่ยนแปลงพารามิเตอร์เหล่านี้

ต้นทุนเฉลี่ยจะคำนวณโดยใช้สูตรต่อไปนี้:

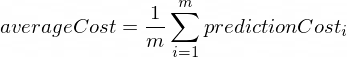
โดยที่ m คือตัวอย่างการฝึกอบรมจำนวนหนึ่ง (ในกรณีของเรา: 100 )

นี่คือวิธีที่เราอาจนำไปใช้ในโค้ด:

 function forwardPropagation ( model , xTrain , yTrain ) {
  const m = xTrain . length ;
  const predictions = [ ] ;
  let cost = 0 ;
  for ( let i = 0 ; i < m ; i += 1 ) {
    const prediction = nanoNeuron . predict ( xTrain [ i ] ) ;
    cost += predictionCost ( yTrain [ i ] , prediction ) ;
    predictions . push ( prediction ) ;
  }
  // We are interested in average cost.
  cost /= m ;
  return [ predictions , cost ] ;
}

การขยายพันธุ์แบบย้อนกลับ

เมื่อเรารู้ว่าการคาดการณ์ของ NanoNeuron ถูกหรือผิด (โดยอิงจากต้นทุนเฉลี่ย ณ จุดนี้) เราควรทำอย่างไรเพื่อให้การคาดการณ์แม่นยำยิ่งขึ้น

การขยายพันธุ์แบบย้อนกลับทำให้เรามีคำตอบสำหรับคำถามนี้ การแพร่กระจายแบบย้อนกลับเป็นกระบวนการประเมินต้นทุนของการทำนายและการปรับพารามิเตอร์ของ NanoNeuron w และ b เพื่อให้การคาดการณ์ครั้งต่อไปและในอนาคตแม่นยำยิ่งขึ้น

นี่คือสถานที่ที่แมชชีนเลิร์นนิงดูเหมือนเป็นเวทมนตร์ ?‍♂️ แนวคิดหลักที่นี่คือ อนุพันธ์ ซึ่งแสดงขั้นตอนที่ต้องดำเนินการเพื่อให้เข้าใกล้ฟังก์ชันต้นทุนขั้นต่ำที่สุด

โปรดจำไว้ว่าการค้นหาฟังก์ชันต้นทุนขั้นต่ำคือเป้าหมายสูงสุดของกระบวนการฝึกอบรม หากเราพบว่าค่าของ w และ b ทำให้ฟังก์ชันต้นทุนเฉลี่ยของเรามีค่าน้อย นั่นหมายความว่าโมเดล NanoNeuron สามารถคาดการณ์ได้ดีและแม่นยำมาก

อนุพันธ์เป็นหัวข้อใหญ่และแยกจากกันซึ่งเราจะไม่กล่าวถึงในบทความนี้ MathIsFun เป็นแหล่งข้อมูลที่ดีในการทำความเข้าใจขั้นพื้นฐาน

สิ่งหนึ่งที่เกี่ยวกับอนุพันธ์ที่จะช่วยให้คุณเข้าใจว่าการแพร่กระจายแบบย้อนกลับทำงานอย่างไร อนุพันธ์ตามความหมายแล้วคือเส้นสัมผัสเส้นโค้งของฟังก์ชันที่ชี้ไปยังทิศทางของฟังก์ชันขั้นต่ำ

แหล่งที่มาของภาพ: MathIsFun

ตัวอย่างเช่น จากแผนภาพด้านบน คุณจะเห็นว่าหากเราอยู่ที่จุด (x=2, y=4) แล้วความชันจะบอกให้เราไป left และ down เพื่อไปยังจุดต่ำสุดของฟังก์ชัน โปรดสังเกตด้วยว่ายิ่งความชันมากเท่าไร เราก็ควรเคลื่อนที่ให้ถึงจุดต่ำสุดเร็วขึ้นเท่านั้น

อนุพันธ์ของฟังก์ชัน averageCost ของเราสำหรับพารามิเตอร์ w และ b มีลักษณะดังนี้:

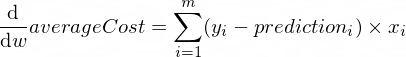
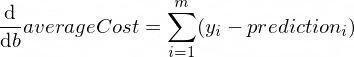
โดยที่ m คือตัวอย่างการฝึกอบรมจำนวนหนึ่ง (ในกรณีของเรา: 100 )

คุณสามารถอ่านเพิ่มเติมเกี่ยวกับกฎอนุพันธ์และวิธีหาอนุพันธ์ของฟังก์ชันที่ซับซ้อนได้ที่นี่

 function backwardPropagation ( predictions , xTrain , yTrain ) {
  const m = xTrain . length ;
  // At the beginning we don't know in which way our parameters 'w' and 'b' need to be changed.
  // Therefore we're setting up the changing steps for each parameters to 0.
  let dW = 0 ;
  let dB = 0 ;
  for ( let i = 0 ; i < m ; i += 1 ) {
    dW += ( yTrain [ i ] - predictions [ i ] ) * xTrain [ i ] ;
    dB += yTrain [ i ] - predictions [ i ] ;
  }
  // We're interested in average deltas for each params.
  dW /= m ;
  dB /= m ;
  return [ dW , dB ] ;
}

การฝึกอบรมโมเดล

ตอนนี้เรารู้วิธีประเมินความถูกต้องของแบบจำลองของเราสำหรับตัวอย่างชุดการฝึกทั้งหมด ( การเผยแพร่ไปข้างหน้า ) นอกจากนี้เรายังรู้วิธีปรับเปลี่ยนพารามิเตอร์ w และ b เล็กน้อยของโมเดล NanoNeuron ของเรา ( การเผยแพร่แบบย้อนกลับ ) แต่ปัญหาคือถ้าเราเรียกใช้การเผยแพร่ไปข้างหน้าแล้วจึงเผยแพร่ย้อนหลังเพียงครั้งเดียว โมเดลของเราจะไม่เพียงพอในการเรียนรู้กฎ/แนวโน้มจากข้อมูลการฝึกอบรม คุณอาจเปรียบเทียบกับการเข้าเรียนโรงเรียนประถมศึกษาหนึ่งวันสำหรับเด็กก็ได้ เขา/เธอควรจะไปโรงเรียนไม่ใช่แค่ครั้งเดียว แต่วันแล้ววันเล่าปีแล้วปีเล่าเพื่อเรียนรู้บางสิ่งบางอย่าง

ดังนั้นเราจึงจำเป็นต้องทำซ้ำการเผยแพร่ไปข้างหน้าและข้างหลังสำหรับโมเดลของเราหลายครั้ง นั่นคือสิ่งที่ฟังก์ชัน trainModel() ทำ มันเหมือนกับ "ครู" สำหรับโมเดล NanoNeuron ของเรา:

• มันจะใช้เวลา ( epochs ) กับโมเดล NanoNeuron ที่โง่เขลาเล็กน้อยของเราและพยายามฝึก / สอนมัน
• มันจะใช้ "หนังสือ" เฉพาะ (ชุดข้อมูล xTrain และ yTrain ) สำหรับการฝึกอบรม
• มันจะผลักดันให้ลูกของเราเรียนรู้มากขึ้น (เร็วขึ้น) โดยใช้พารามิเตอร์อัตราการเรียนรู้ alpha

คำไม่กี่คำเกี่ยวกับอัตราการเรียนรู้ alpha นี่เป็นเพียงตัวคูณสำหรับค่า dW และ dB ที่เราคำนวณระหว่างการขยายพันธุ์แบบย้อนกลับ ดังนั้นอนุพันธ์จึงชี้เราไปในทิศทางที่เราต้องใช้เพื่อค้นหาฟังก์ชันต้นทุนขั้นต่ำ (เครื่องหมาย dW และ dB ) และยังแสดงให้เราเห็นว่าเราต้องไปเร็วแค่ไหนในทิศทางนั้น (ค่าสัมบูรณ์ของ dW และ dB ) ตอนนี้เราต้องคูณขนาดขั้นตอนเหล่านั้นเป็น alpha เพียงเพื่อปรับการเคลื่อนไหวของเราให้เร็วขึ้นหรือช้าลง บางครั้งหากเราใช้ค่าสูงสำหรับ alpha เราอาจกระโดดข้ามค่าต่ำสุดแล้วไม่พบเลย

การเปรียบเทียบกับครูก็คือ ยิ่งเขา/เธอผลัก "เด็กนาโน" ของเราแรงขึ้นเท่าไร "เด็กนาโน" ของเราก็จะเรียนรู้ได้เร็วยิ่งขึ้นเท่านั้น แต่ถ้าครูผลักแรงเกินไป "เด็ก" ก็จะมีอาการทางประสาทและชนะ ไม่สามารถเรียนรู้อะไรได้เลยใช่ไหม?

นี่คือวิธีที่เราจะอัปเดตพารามิเตอร์ w และ b ของโมเดลของเรา:

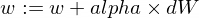
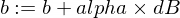
และนี่คือฟังก์ชันเทรนเนอร์ของเรา:

 function trainModel ( { model , epochs , alpha , xTrain , yTrain } ) {
  // The is the history array of how NanoNeuron learns.
  const costHistory = [ ] ;

  // Let's start counting epochs.
  for ( let epoch = 0 ; epoch < epochs ; epoch += 1 ) {
    // Forward propagation.
    const [ predictions , cost ] = forwardPropagation ( model , xTrain , yTrain ) ;
    costHistory . push ( cost ) ;
  
    // Backward propagation.
    const [ dW , dB ] = backwardPropagation ( predictions , xTrain , yTrain ) ;
  
    // Adjust our NanoNeuron parameters to increase accuracy of our model predictions.
    nanoNeuron . w += alpha * dW ;
    nanoNeuron . b += alpha * dB ;
  }

  return costHistory ;
}

นำชิ้นส่วนทั้งหมดมารวมกัน

ตอนนี้เรามาใช้ฟังก์ชันที่เราสร้างขึ้นด้านบนกันดีกว่า

มาสร้างอินสแตนซ์โมเดล NanoNeuron ของเรากันดีกว่า ในขณะนี้ NanoNeuron ไม่ทราบว่าควรตั้งค่าใดสำหรับพารามิเตอร์ w และ b ลองตั้งค่า w และ b แบบสุ่มกัน

 const w = Math . random ( ) ; // i.e. -> 0.9492
const b = Math . random ( ) ; // i.e. -> 0.4570
const nanoNeuron = new NanoNeuron ( w , b ) ;

สร้างชุดข้อมูลการฝึกอบรมและทดสอบ

 const [ xTrain , yTrain , xTest , yTest ] = generateDataSets ( ) ;

มาฝึกโมเดลด้วยขั้นตอนที่เพิ่มขึ้นเล็กน้อย ( 0.0005 ) สำหรับ 70000 epoch คุณสามารถเล่นกับพารามิเตอร์เหล่านี้ได้ โดยจะมีการกำหนดไว้เชิงประจักษ์

 const epochs = 70000 ;
const alpha = 0.0005 ;
const trainingCostHistory = trainModel ( { model : nanoNeuron , epochs , alpha , xTrain , yTrain } ) ;

เรามาตรวจสอบว่าฟังก์ชันต้นทุนเปลี่ยนแปลงไปอย่างไรในระหว่างการฝึกอบรม เราคาดว่าค่าใช้จ่ายหลังการฝึกอบรมน่าจะต่ำกว่าเมื่อก่อนมาก นี่หมายความว่า NanoNeuron ฉลาดขึ้น ตรงกันข้ามก็เป็นไปได้เช่นกัน

 console . log ( 'Cost before the training:' , trainingCostHistory [ 0 ] ) ; // i.e. -> 4694.3335043
console . log ( 'Cost after the training:' , trainingCostHistory [ epochs - 1 ] ) ; // i.e. -> 0.0000024

นี่คือการเปลี่ยนแปลงค่าใช้จ่ายในการฝึกอบรมในยุคต่างๆ บนแกน x คือเลขยุค x1000

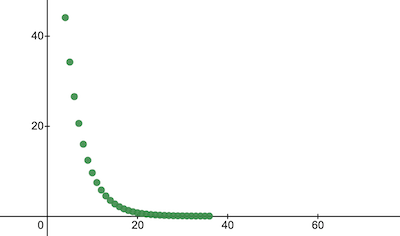
มาดูพารามิเตอร์ของ NanoNeuron เพื่อดูว่าได้เรียนรู้อะไรบ้าง เราคาดหวังว่าพารามิเตอร์ NanoNeuron w และ b จะคล้ายกับพารามิเตอร์ที่เรามีในฟังก์ชัน celsiusToFahrenheit() ( w = 1.8 และ b = 32 ) เนื่องจาก NanoNeuron ของเราพยายามเลียนแบบ

 console . log ( 'NanoNeuron parameters:' , { w : nanoNeuron . w , b : nanoNeuron . b } ) ; // i.e. -> {w: 1.8, b: 31.99}

ประเมินความแม่นยำของแบบจำลองสำหรับชุดข้อมูลทดสอบเพื่อดูว่า NanoNeuron ของเราจัดการกับการคาดการณ์ข้อมูลที่ไม่รู้จักใหม่ๆ ได้ดีเพียงใด คาดว่าต้นทุนการทำนายชุดทดสอบจะใกล้เคียงกับต้นทุนการฝึกอบรม นี่หมายความว่า NanoNeuron ของเราทำงานได้ดีกับข้อมูลที่รู้จักและไม่รู้จัก

 [ testPredictions , testCost ] = forwardPropagation ( nanoNeuron , xTest , yTest ) ;
console . log ( 'Cost on new testing data:' , testCost ) ; // i.e. -> 0.0000023

ตอนนี้ เนื่องจากเราเห็นว่า "เด็ก" NanoNeuron ของเราทำงานได้ดีใน "โรงเรียน" ในระหว่างการฝึก และเขาสามารถแปลงอุณหภูมิเซลเซียสเป็นฟาเรนไฮต์ได้อย่างถูกต้อง แม้ว่าข้อมูลจะไม่ได้เห็น เราก็สามารถเรียกมันว่า "อัจฉริยะ" ได้ และถามคำถามบางอย่างกับเขา นี่เป็นเป้าหมายสูงสุดของกระบวนการฝึกอบรมทั้งหมด

 const tempInCelsius = 70 ;
const customPrediction = nanoNeuron . predict ( tempInCelsius ) ;
console . log ( `NanoNeuron "thinks" that ${ tempInCelsius } °C in Fahrenheit is:` , customPrediction ) ; // -> 158.0002
console . log ( 'Correct answer is:' , celsiusToFahrenheit ( tempInCelsius ) ) ; // -> 158

ใกล้แล้ว! ในฐานะมนุษย์เราทุกคน NanoNeuron ของเรานั้นดีแต่ไม่เหมาะ :)

ขอให้มีความสุขกับการเรียนรู้!

วิธีเปิดใช้งาน NanoNeuron

คุณสามารถโคลนพื้นที่เก็บข้อมูลและรันในเครื่องได้:

git clone https://github.com/trekhleb/nano-neuron.git
cd nano-neuron

node ./NanoNeuron.js

ข้ามแนวคิดการเรียนรู้ของเครื่อง

แนวคิดแมชชีนเลิร์นนิงต่อไปนี้ถูกข้ามและทำให้ง่ายขึ้นเพื่อให้อธิบายได้ง่าย

การฝึกอบรม/การทดสอบการแยกชุดข้อมูล

โดยปกติแล้วคุณจะมีชุดข้อมูลขนาดใหญ่ชุดเดียว ขึ้นอยู่กับจำนวนตัวอย่างในชุดนั้น คุณอาจต้องการแบ่งออกเป็นสัดส่วน 70/30 สำหรับชุดฝึก/ชุดทดสอบ ข้อมูลในชุดควรสุ่มสับก่อนแยก หากจำนวนตัวอย่างมีขนาดใหญ่ (เช่น ล้าน) การแยกอาจเกิดขึ้นในสัดส่วนที่ใกล้กับ 90/10 หรือ 95/5 สำหรับชุดข้อมูลฝึก/ทดสอบ

เครือข่ายนำพลังมา

โดยปกติแล้วคุณจะไม่สังเกตเห็นการใช้เซลล์ประสาทแบบสแตนด์อโลนเพียงเซลล์เดียว พลังอยู่ในเครือข่ายของเซลล์ประสาทดังกล่าว เครือข่ายอาจเรียนรู้คุณสมบัติที่ซับซ้อนกว่านี้มาก NanoNeuron เพียงอย่างเดียวดูเหมือนเป็นการถดถอยเชิงเส้นอย่างง่ายมากกว่าโครงข่ายประสาทเทียม

อินพุตการทำให้เป็นมาตรฐาน

ก่อนการฝึกอบรม การปรับค่าอินพุตให้เป็นมาตรฐานจะดีกว่า

การใช้งานแบบเวกเตอร์

สำหรับเครือข่าย การคำนวณแบบเวกเตอร์ (เมทริกซ์) จะทำงานเร็วกว่า for วนซ้ำมาก โดยปกติแล้วการเผยแพร่ไปข้างหน้า/ย้อนกลับจะทำงานได้เร็วกว่ามากหากนำไปใช้ในรูปแบบเวกเตอร์และคำนวณโดยใช้ เช่น ไลบรารี Numpy Python

ฟังก์ชันต้นทุนขั้นต่ำ

ฟังก์ชันต้นทุนที่เราใช้ในตัวอย่างนี้เป็นแบบเรียบง่ายเกินไป ควรมีส่วนประกอบลอการิทึม การเปลี่ยนฟังก์ชันต้นทุนจะเปลี่ยนอนุพันธ์ด้วย ดังนั้นขั้นตอนการขยายพันธุ์ด้านหลังจะใช้สูตรที่แตกต่างกัน

ฟังก์ชั่นการเปิดใช้งาน

โดยปกติแล้วเอาต์พุตของเซลล์ประสาทควรถูกส่งผ่านฟังก์ชันกระตุ้น เช่น Sigmoid หรือ ReLU หรืออื่นๆ

ผู้เขียน

• @trekhleb