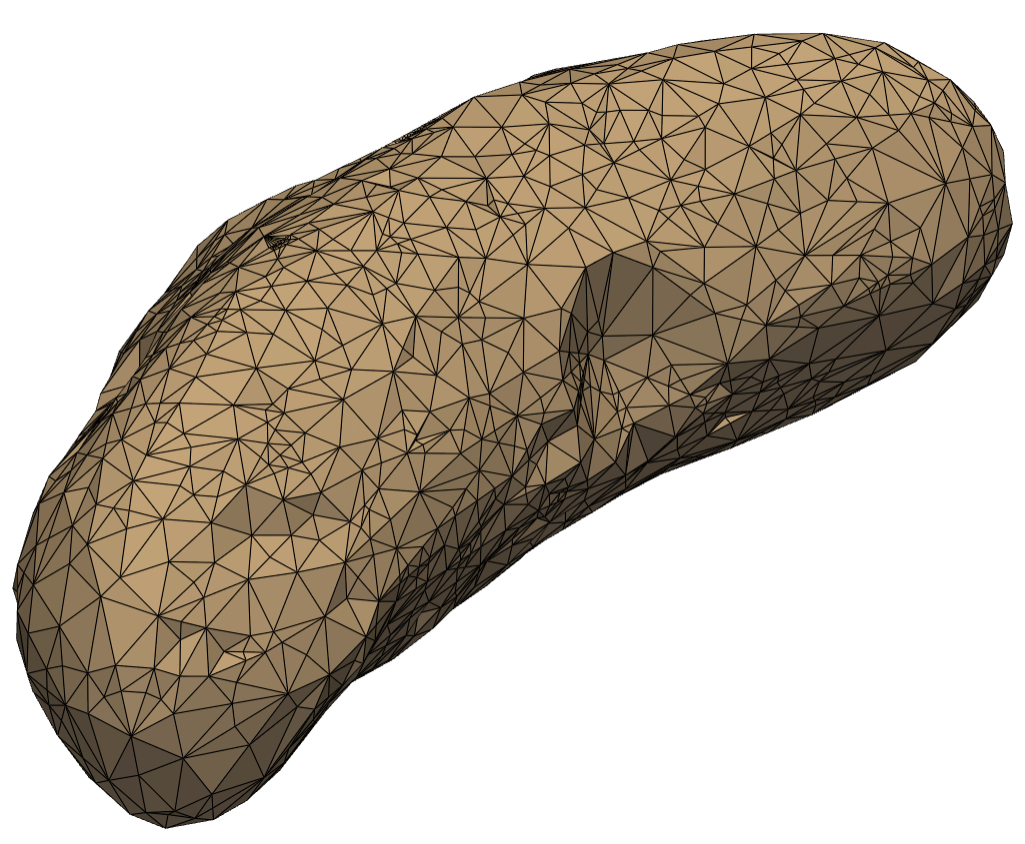
ตาข่ายของ (433) Eros ที่มี 739 จุดยอดและ 1474 ใบหน้า
รหัสนี้เป็นการใช้งานที่ผ่านการตรวจสอบความถูกต้องใน C ++ 17 ของแบบจำลองแรงโน้มถ่วงหลายรูปแบบโดย Tsoulis และคณะนอกจากนี้โมเดลยังให้การผูกมัด Python มันถูกสร้างขึ้นในขั้นต้นในโครงการความร่วมมือระหว่างทีมแนวคิดขั้นสูงของ Tu Munich และ ESA
หากการใช้งานนี้พิสูจน์ได้ว่าเป็นประโยชน์สำหรับคุณโปรดพิจารณาอ้างถึงเอกสารประกอบที่ตีพิมพ์ใน วารสารซอฟต์แวร์โอเพ่นซอร์ส
การดำเนินการขึ้นอยู่กับกระดาษ Tsoulis, D. , 2012 การคำนวณเชิงวิเคราะห์ของแรงโน้มถ่วงแบบเต็มของแรงโน้มถ่วงแบบเต็มรูปแบบของแหล่งโพลีเฮดที่มีรูปทรงเป็นเนื้อเดียวกันโดยใช้อินทิกรัลเส้น ธรณีฟิสิกส์, 77 (2), pp.f1-F11 และการใช้งานที่สอดคล้องกันใน Fortran
รายละเอียดเพิ่มเติมสามารถพบได้ในกระดาษล่าสุด Tsoulis, Dimitrios; Gavriilidou, Georgia การทบทวนการคำนวณของสูตรการวิเคราะห์อินทิกรัลของสัญญาณแรงโน้มถ่วงหลายรูปแบบ การสำรวจทางธรณีฟิสิกส์, 2021, 69. Jg., nr. 8-9, S. 1745-1760 และการใช้งานที่สอดคล้องกันใน MATLAB ซึ่งขึ้นอยู่กับการใช้งานเดิมใน Fortran
บันทึก
หน้า GitHub ของโครงการนี้มีเอกสารประกอบเต็มรูปแบบของไลบรารี C ++ และอินเทอร์เฟซ Python รวมถึงพื้นหลังในโมเดลแรงโน้มถ่วงและการตั้งค่าขั้นสูงที่ไม่ได้มีรายละเอียดที่นี่
การประเมินผลของแบบจำลองแรงโน้มถ่วงหลายรูปแบบต้องใช้พารามิเตอร์ต่อไปนี้:
| ชื่อ |
|---|
| ตาข่ายหลายรูป |
| ความหนาแน่นคงที่ |
ตาข่ายและความหนาแน่นของค่าคงที่จะต้องตรงกัน ดูเอกสารเพื่อดูไฟล์ตาข่ายที่รองรับ
การคำนวณเอาต์พุตพารามิเตอร์ต่อไปนี้สำหรับทุกจุดคำนวณ p หน่วยของเอาต์พุตที่เกี่ยวข้องขึ้นอยู่กับหน่วยของพารามิเตอร์อินพุต (ตาข่ายและความหนาแน่น)! ดังนั้นถ้าเช่นตาข่ายของคุณอยู่ใน
| ชื่อ | หน่วย (ถ้าตาข่ายใน | การแสดงความคิดเห็น |
|---|---|---|
| ศักยภาพหรือเรียกว่าพลังงานเฉพาะ | ||
| การเร่งรัดแรงโน้มถ่วงในสามทิศทางคาร์ทีเซียน | ||
| อัตราการเปลี่ยนแปลงของการเปลี่ยนแปลงแรงโน้มถ่วง |
บันทึก
ผลผลิตของโมเดลแรงโน้มถ่วงนี้เชื่อในการประชุมทางธรณีวิทยาและธรณีฟิสิกส์ ดังนั้นศักยภาพ
ตัวอย่างต่อไปนี้แสดงวิธีใช้อินเทอร์เฟซ Python เพื่อคำนวณแรงโน้มถ่วงรอบลูกบาศก์:
import numpy as np
from polyhedral_gravity import Polyhedron , GravityEvaluable , evaluate , PolyhedronIntegrity , NormalOrientation
# We define the cube as a polyhedron with 8 vertices and 12 triangular faces
# The polyhedron's normals point outwards (see below for checking this)
# The density is set to 1.0
cube_vertices = np . array (
[[ - 1 , - 1 , - 1 ], [ 1 , - 1 , - 1 ], [ 1 , 1 , - 1 ], [ - 1 , 1 , - 1 ],
[ - 1 , - 1 , 1 ], [ 1 , - 1 , 1 ], [ 1 , 1 , 1 ], [ - 1 , 1 , 1 ]]
)
cube_faces = np . array (
[[ 1 , 3 , 2 ], [ 0 , 3 , 1 ], [ 0 , 1 , 5 ], [ 0 , 5 , 4 ], [ 0 , 7 , 3 ], [ 0 , 4 , 7 ],
[ 1 , 2 , 6 ], [ 1 , 6 , 5 ], [ 2 , 3 , 6 ], [ 3 , 7 , 6 ], [ 4 , 5 , 6 ], [ 4 , 6 , 7 ]]
)
cube_density = 1.0
computation_point = np . array ([ 0 , 0 , 0 ]) ก่อนอื่นเรากำหนดรูปทรงหลายเหลี่ยมความหนาแน่นคงที่จาก vertices และ faces
cube_polyhedron = Polyhedron (
polyhedral_source = ( cube_vertices , cube_faces ),
density = cube_density ,
) ในกรณีที่คุณต้องการส่งมอบโพลีเฮดตรอนผ่านรูปแบบไฟล์ที่รองรับเพียงแทนที่อาร์กิวเมนต์ polyhedral_source ด้วย รายการสตริง แต่ละสตริงเป็นเส้นทางไปยังรูปแบบไฟล์ที่รองรับเช่น polyhedral_source=["eros.node","eros.face"] หรือ polyhedral_source=["eros.mesh"]
ต่อเนื่องวิธีที่ง่ายที่สุดในการคำนวณแรงโน้มถ่วงคือการใช้ฟังก์ชั่น evaluate :
potential , acceleration , tensor = evaluate (
polyhedron = cube_polyhedron ,
computation_points = computation_point ,
parallel = True ,
) วิธีที่ก้าวหน้ายิ่งขึ้นคือการใช้คลาส GravityEvaluable มันแคชโครงสร้างข้อมูลภายในและคุณสมบัติซึ่งสามารถนำกลับมาใช้ใหม่สำหรับการประเมินหลายครั้ง สิ่งนี้มีประโยชน์อย่างยิ่งหากคุณต้องการคำนวณแรงโน้มถ่วงสำหรับจุดคำนวณหลายจุด แต่ไม่ทราบว่า "คะแนนในอนาคต" ล่วงหน้า
evaluable = GravityEvaluable ( polyhedron = cube_polyhedron ) # stores intermediate computation steps
potential , acceleration , tensor = evaluable (
computation_points = computation_point ,
parallel = True ,
)
# Any future evaluable call after this one will be faster โปรดทราบว่า computation_point อาจเป็น (n, 3) อาร์เรย์รูปทรงเพื่อคำนวณหลายจุดในครั้งเดียว ในกรณีนี้ค่าผลตอบแทนของ evaluate(..) หรือ GravityEvaluable จะเป็นรายการของแฝดสามซึ่งประกอบด้วยศักยภาพการเร่งความเร็วและเทนเซอร์
แบบจำลองแรงโน้มถ่วงต้องการให้บรรทัดฐานของหน่วยระนาบของโพลีเฮดตรอนทั้งหมดชี้ไปด้านนอกอย่างสม่ำเสมอหรือด้านในรูปทรงหลายเหลี่ยม คุณสามารถระบุสิ่งนี้ผ่าน normal_orientation คุณสมบัตินี้คือ - โดยค่าเริ่มต้น - ตรวจสอบเมื่อสร้าง Polyhedron ! ดังนั้นไม่ต้องกังวลมันเป็นไปไม่ได้หากไม่ปิดใช้งาน อย่างชัดเจน เพื่อสร้าง Polyhedron ที่ไม่ถูกต้อง คุณสามารถปิดการใช้งาน/ เปิดใช้งานการตั้งค่านี้ผ่าน Flag integrity_check เสริมและยังสามารถซ่อมแซมการสั่งซื้อผ่าน HEAL โดยอัตโนมัติ หากคุณมั่นใจว่าตาข่ายของคุณถูกกำหนดอย่างถูกต้อง (เช่นตรวจสอบหนึ่งครั้งด้วยการตรวจสอบความสมบูรณ์) คุณสามารถปิดการใช้งานการตรวจสอบนี้ (ผ่าน DISABLE ) เพื่อหลีกเลี่ยงค่าใช้จ่ายรันไทม์เพิ่มเติมของเช็ค
cube_polyhedron = Polyhedron (
polyhedral_source = ( cube_vertices , cube_faces ),
density = cube_density ,
normal_orientation = NormalOrientation . INWARDS , # OUTWARDS (default) or INWARDS
integrity_check = PolyhedronIntegrity . VERIFY , # VERIFY (default), DISABLE or HEAL
)เคล็ดลับ
ตัวอย่างและแปลงเพิ่มเติมแสดงไว้ในสมุดบันทึก Jupyter
ตัวอย่างต่อไปนี้แสดงวิธีใช้ไลบรารี C ++ เพื่อคำนวณแรงโน้มถ่วง มันทำงานแบบอะนาล็อกกับตัวอย่าง Python ด้านบน
// Defining the input like above in the Python example
std::vector<std::array< double , 3 >> vertices = ...
std::vector<std::array< size_t , 3 >> faces = ...
double density = 1.0 ;
// The constant density polyhedron is defined by its vertices & faces
// It also supports the hand-over of NormalOrientation and PolyhedronIntegrity as optional arguments
// as above described for the Python Interface
Polyhedron polyhedron{vertices, faces, density};
std::vector<std::array< double , 3 >> points = ...
std::array< double , 3 > point = points[ 0 ];
bool parallel = true ; ไลบรารี C ++ มีสองวิธีในการคำนวณแรงโน้มถ่วง ผ่านฟังก์ชั่นฟรี evaluate ...
const auto [pot, acc, tensor] = GravityModel::evaluate(polyhedron, point, parallel); ... หรือผ่านชั้นเรียน GravityEvaluable
// Instantiation of the GravityEvaluable object
GravityEvaluable evaluable{polyhedron};
// From now, we can evaluate the gravity model for any point with
const auto [potential, acceleration, tensor] = evaluable(point, parallel);
// or for multiple points with
const auto results = evaluable(points, parallel);ในทำนองเดียวกันกับ Python การใช้งาน C ++ ยังให้ความสามารถในการตรวจสอบตาข่าย
เคล็ดลับ
สำหรับการอ้างอิงให้ดูที่วิธีการหลักของการปฏิบัติการ C ++
อินเทอร์เฟซ Python สามารถติดตั้งได้อย่างง่ายดายด้วย conda:
conda install -c conda-forge polyhedral-gravity-modelเป็นตัวเลือกที่สองคุณยังสามารถติดตั้งอินเทอร์เฟซ Python ด้วย PIP จาก PYPI
pip install polyhedral-gravity ไบนารีสำหรับแพลตฟอร์มที่พบมากที่สุดมีอยู่ใน PYPI รวมถึง Windows, Linux และ MacOS สำหรับ MacOS และ Linux จะมีการจัดอันดับไบนารีสำหรับ x86_64 และ aarch64 ในกรณีที่ pip ใช้การแจกจ่ายแหล่งที่มาโปรดตรวจสอบให้แน่ใจว่าคุณมีคอมไพเลอร์ที่มีความสามารถ C ++ 17 ที่ติดตั้ง CMAKE
โครงการใช้การพึ่งพาต่อไปนี้ทั้งหมดจะถูกตั้งค่า โดยอัตโนมัติ ผ่าน CMake:
atan(..)โมดูลจะสร้างโดยใช้คอมไพเลอร์ C ++ 17 ที่มีความสามารถ CMake เพียงดำเนินการคำสั่งต่อไปนี้ในโฟลเดอร์รูทที่เก็บ:
pip install . ในการปรับเปลี่ยนตัวเลือกการสร้าง (เช่นการขนาน) ให้ดูที่ย่อหน้าถัดไป ตัวเลือกจะถูกแก้ไขโดยการตั้งค่าตัวแปรสภาพแวดล้อมก่อนที่จะดำเนิน pip install . คำสั่งเช่น:
export POLYHEDRAL_GRAVITY_PARALLELIZATION= " TBB "
pip install .(ตัวเลือก: สำหรับการสร้างที่เร็วขึ้นคุณสามารถติดตั้งการพึ่งพาทั้งหมดที่มีอยู่สำหรับระบบของคุณในสภาพแวดล้อม Python ในพื้นที่ของคุณด้วยวิธีนั้นพวกเขาจะไม่ถูกดึงมาจาก GitHub)
โปรแกรมสร้างขึ้นโดยใช้ CMake ก่อนอื่นให้แน่ใจว่าคุณติดตั้ง CMake จากนั้นทำตามขั้นตอนเหล่านี้:
mkdir build
cd build
cmake .. < options >
cmake --build .มีตัวเลือกต่อไปนี้:
| ชื่อ (ค่าเริ่มต้น) | ตัวเลือก |
|---|---|
polyhedral_gravity_parallelization ( CPP ) | CPP = การดำเนินการแบบอนุกรม / OMP หรือ TBB = การดำเนินการแบบขนานกับ TBB ของ OpenMP หรือ Intel |
Logging_level ( INFO ) | TRACE , DEBUG , INFO , WARN , ERROR , CRITICAL , OFF |
build_polyhedral_gravity_docs ( OFF ) | สร้างเอกสารนี้ |
build_polyhedral_gravity_tests ( ON ) | สร้างการทดสอบ |
build_polyhedral_python_interface ( ON ) | สร้างอินเทอร์เฟซ Python |
ในระหว่างการทดสอบ polyhedral_gravity_parallelization = TBB เป็นนักแสดงมากที่สุด ไม่แนะนำให้เปลี่ยน Logging_level เป็นอย่างอื่นนอกเหนือจาก INFO=2
การตั้งค่า CMAKE ที่แนะนำโดยใช้แบ็กเอนด์ TBB จะมีลักษณะเช่นนี้:
cmake .. -POLYHEDRAL_GRAVITY_PARALLELIZATION= " TBB "หลังจากสร้างโมเดลแรงโน้มถ่วงสามารถเรียกใช้ได้โดยการดำเนินการ:
./polyhedralGravity < YAML-Configuration-File > ในกรณีที่ YAML-configuration-file มีพารามิเตอร์ที่ต้องการ ตัวอย่างสำหรับไฟล์การกำหนดค่าและไฟล์ต้นฉบับหลายรูปแบบสามารถพบได้ในพื้นที่เก็บข้อมูลนี้ในโฟลเดอร์ /example-config/
การกำหนดค่าควรมีลักษณะคล้ายกับตัวอย่างที่ระบุไว้ด้านล่าง จำเป็นต้องระบุไฟล์ต้นฉบับของตาข่ายหลายเหลี่ยม (ข้อมูลเพิ่มเติมเกี่ยวกับไฟล์ที่รองรับในเอกสาร) ความหนาแน่นของโพลีเฮดตรอนและจุดคำนวณที่ต้องการซึ่งจะคำนวณเทนเซอร์แรงโน้มถ่วง อีกหนึ่งต้องระบุชื่อของไฟล์เอาต์พุต. csv
---
gravityModel :
input :
polyhedron : # polyhedron source-file(s)
- " ../example-config/data/tsoulis.node " # .node contains the vertices
- " ../example-config/data/tsoulis.face " # .face contains the triangular faces
density : 2670.0 # constant density, units must match with the mesh (see section below)
points : # Location of the computation point(s) P
- [ 0, 0, 0 ] # Here it is situated at the origin
check_mesh : true # Fully optional, enables mesh autodetect+repair of
# the polyhedron's vertex ordering (not given: true)
output :
filename : " gravity_result.csv " # The name of the output file
ปฏิบัติการสร้างไฟล์ CSV ที่มีอยู่
โครงการใช้ googletest สำหรับการทดสอบ ใน Oder เพื่อดำเนินการทดสอบเหล่านั้นเพียงดำเนินการคำสั่งต่อไปนี้ในไดเรกทอรีบิลด์:
ctestสำหรับชุดทดสอบ Python โปรดดำเนินการคำสั่งต่อไปนี้ในโฟลเดอร์รูทที่เก็บ:
pytestเรายินดีที่จะยอมรับการมีส่วนร่วมในโครงการในรูปแบบของคำแนะนำรายงานข้อผิดพลาดและการร้องขอดึง โปรดดูแนวทางการสนับสนุนสำหรับข้อมูลเพิ่มเติม