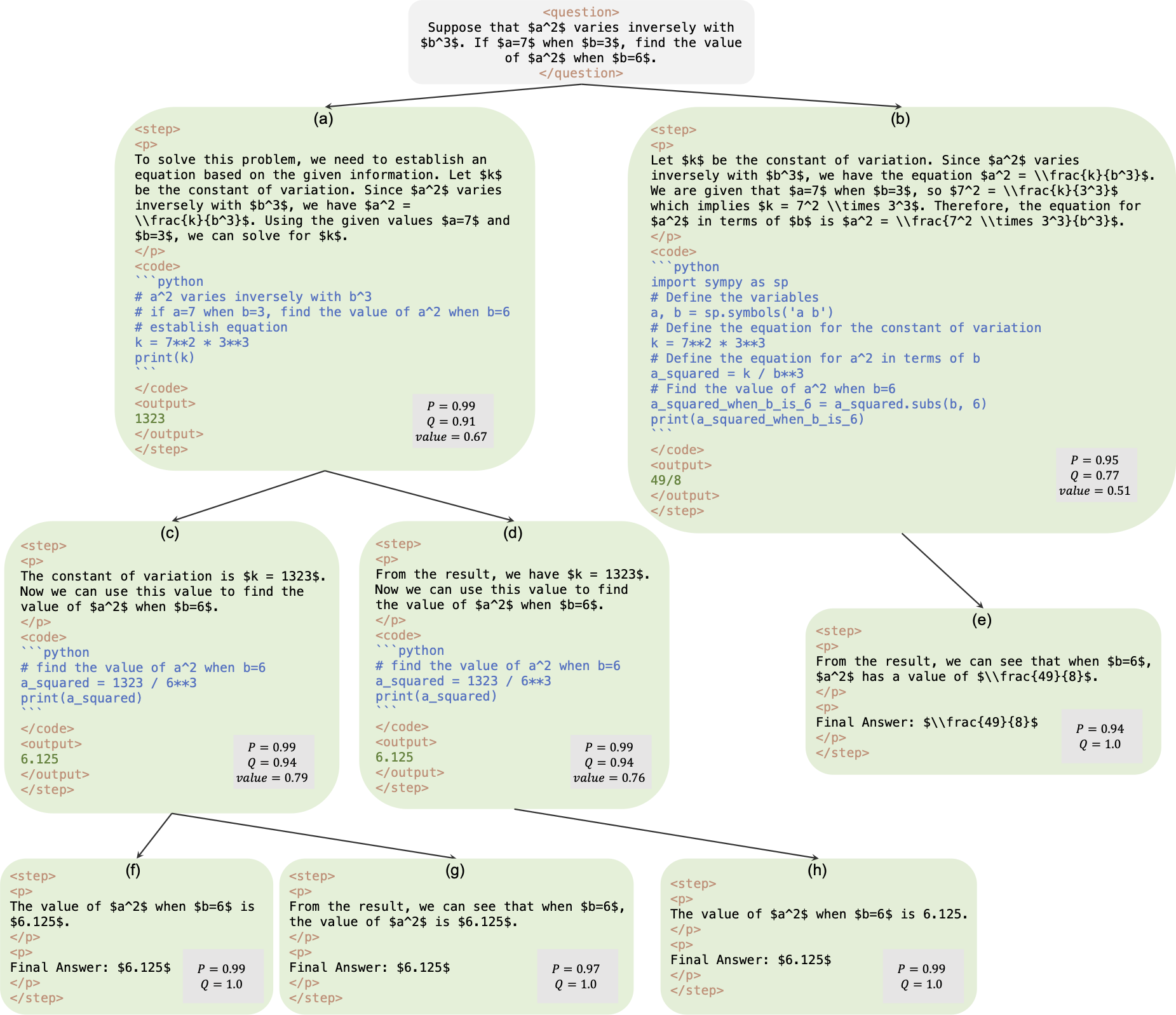
这是论文《AlphaMath 几乎为零：无流程的流程监督》的官方存储库。该代码是从我们内部公司代码库中提取的。因此，在复制我们论文中报告的数字时可能会存在轻微差异，但它们应该非常接近。我们的方法涉及仅使用从蒙特卡罗树搜索 (MCTS) 框架导出的数学推理来训练策略和价值模型，从而消除了对 GPT-4 或人工注释的需要。这是 MCTS 在第 3 轮中生成的训练实例的图示。
检查点：AlphaMath-7B 第 3 轮？ / AlphaMath-7B 第三轮？
数据集：AlphaMath-Round3-Trainset？训练数据的求解过程是根据第2轮中的MCTS和检查点自动生成的。包含正例和负例用于训练策略和价值模型。
训练代码：由于政策原因，我们只能发布一些关键功能的实现细节，基本上应该在你自己的训练代码中进行修改。
| 推理法 | 准确性 | 平均。每 q 的时间（秒） | 平均。步骤 | # 溶胶 |
|---|---|---|---|---|
| 贪婪的 | 53.62 | 1.6 | 3.1 | 1 |
| 少校@5 | 61.84 | 2.9 | 2.9 | 5 |
| 阶梯级梁 (1,5) | 62.32 | 3.1 | 3.0 | 前1名 |
| 5 次运行 + 少校@5 | 67.04 | x5 | x1 | 5 前 1 |
| 阶梯级梁 (2,5) | 64.66 | 2.4 | 2.4 | 前1名 |
| 阶梯梁 (3,5) | 65.74 | 2.3 | 2.2 | 前1名 |
| 阶梯梁 (5,5) | 65.98 | 4.7 | 2.3 | 前1名 |
| 1 次运行 + 少校@5 | 66.54 | x1 | x1 | 前 5 名 |
| 5 次运行 + 少校@5 | 69.94 | x5 | x1 | 5 前 1 |
| MCTS（N = 40） | 64.02 | 10.1 | 3.8 | 前1名 |
+ Maj@5需要运行 5 次，这鼓励了多样性。+ Maj@5直接使用5个候选，缺乏多样性。| 温度 | 0.6 | 1.0 |
|---|---|---|
| 阶梯级梁 (1,5) | 62.32 | 62.76 |
| 阶梯级梁 (2,5) | 64.66 | 65.60 |
| 阶梯梁 (3,5) | 65.74 | 66.28 |
| 阶梯梁 (5,5) | 65.98 | 66.38 |
对于步进级波束搜索，设置temperature=1.0可能会获得稍微更好的结果。
requirements.txt pip install -r requirements.txt
或者简单地按照cmds操作
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e . scripts/save_value_head.py将值头添加到LLM。 您可以运行以下两个命令之一。两者之间的准确度可能略有不同。在我们的机器中，第一个获得了 53.4%，第二个获得了 53.62%。
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
或者
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
在我们的机器上，在 MATH 测试集上，以下配置B1=1, B2=5的 cmd 可以达到 ~62%，配置B1=3, B2=5的 cmd 可以达到 ~65%。
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
计算准确度
python eval_output_jsonl.py
--res_file
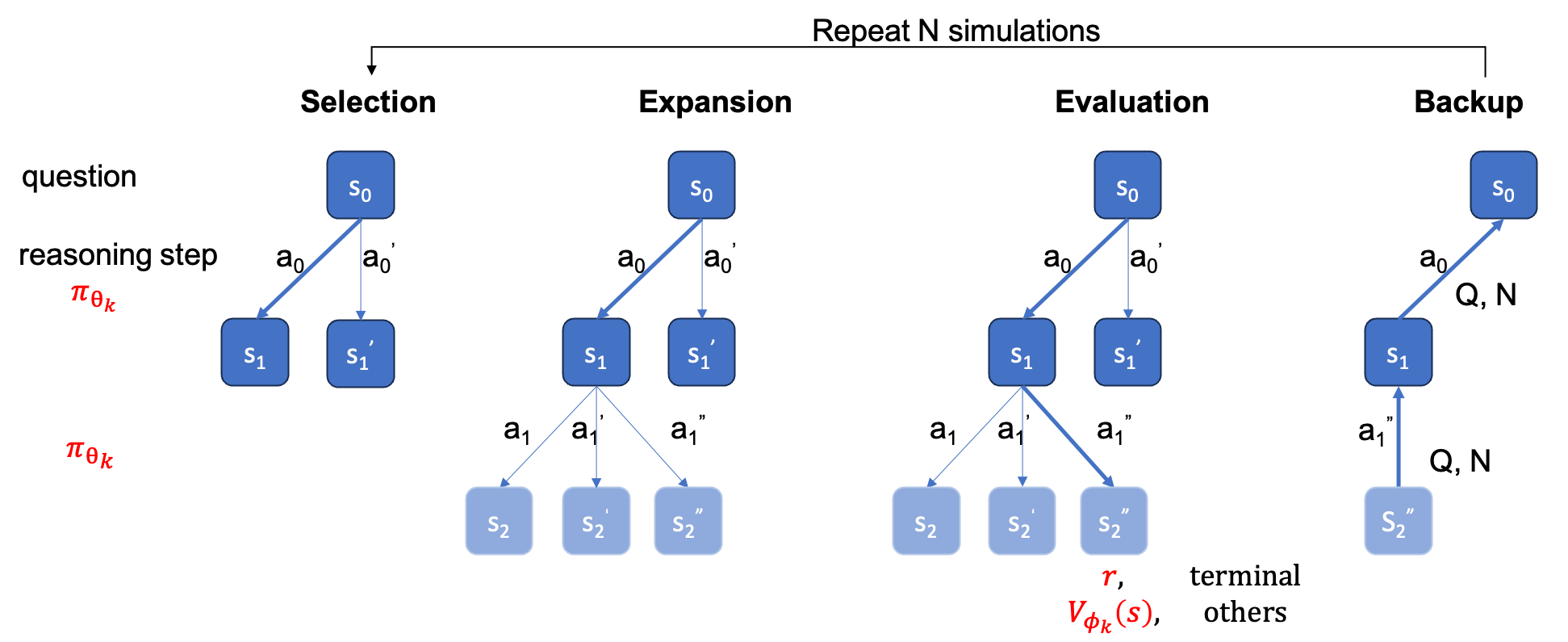
ground_truth （最终答案，不是求解过程）必须在qaf json 或 jsonl 文件中提供（示例格式可以参考../MARIO_EVAL/data/math_testset_annotation.json ）。
第一轮
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
回合 > 1，SFT 后
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
只有question将用于生成解决方案，但ground_truth将用于计算准确性。
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
与步级波束搜索不同，你需要首先构建一棵完整的树，然后你应该离线运行MCTS，然后计算准确性。
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl
注意：此评估脚本也可以通过步骤级波束搜索使用保存的树运行，并且精度应保持相同。
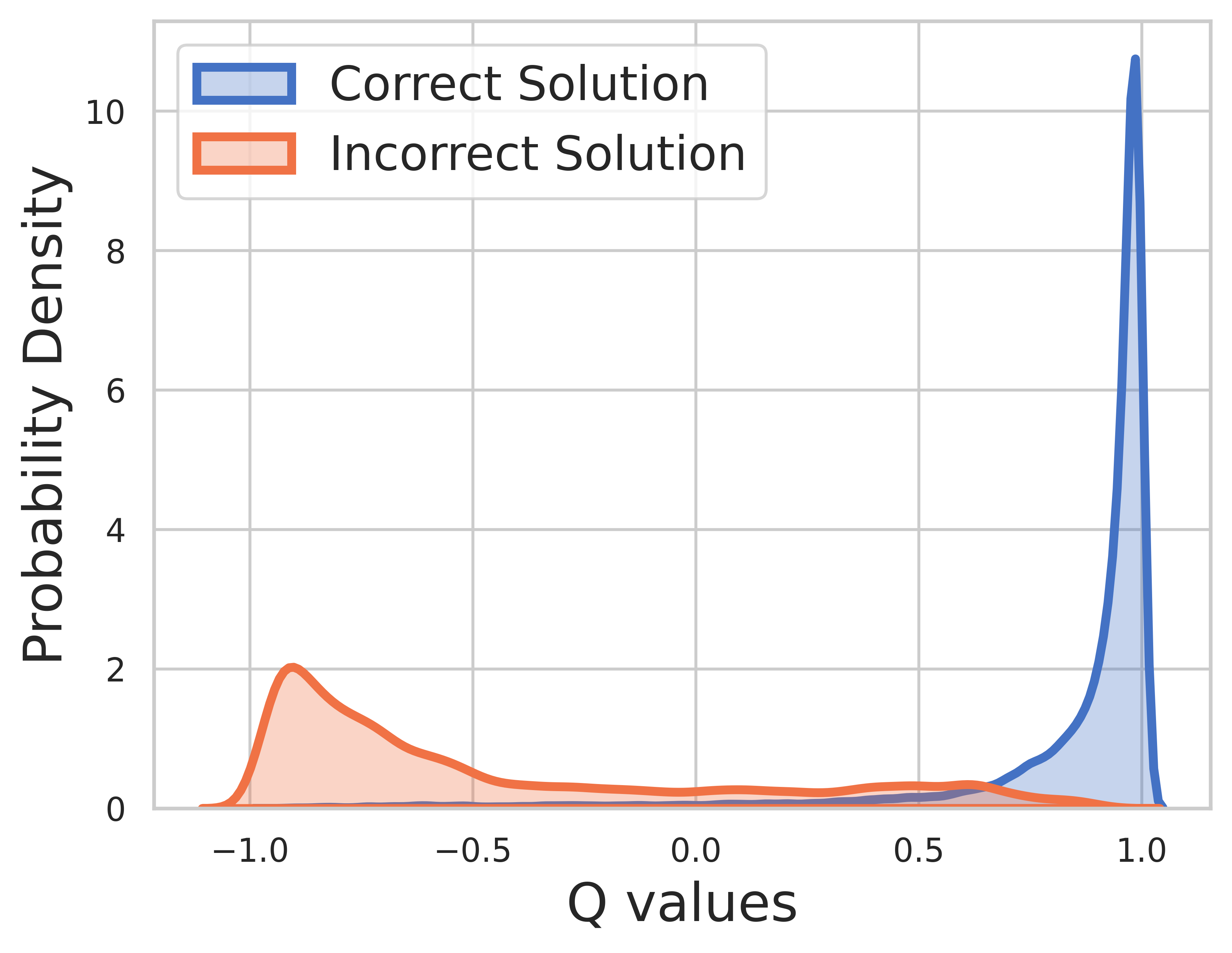
因为训练数据的基本事实是已知的，所以最后一步的值是奖励，并且 Q 值可以很好地收敛。
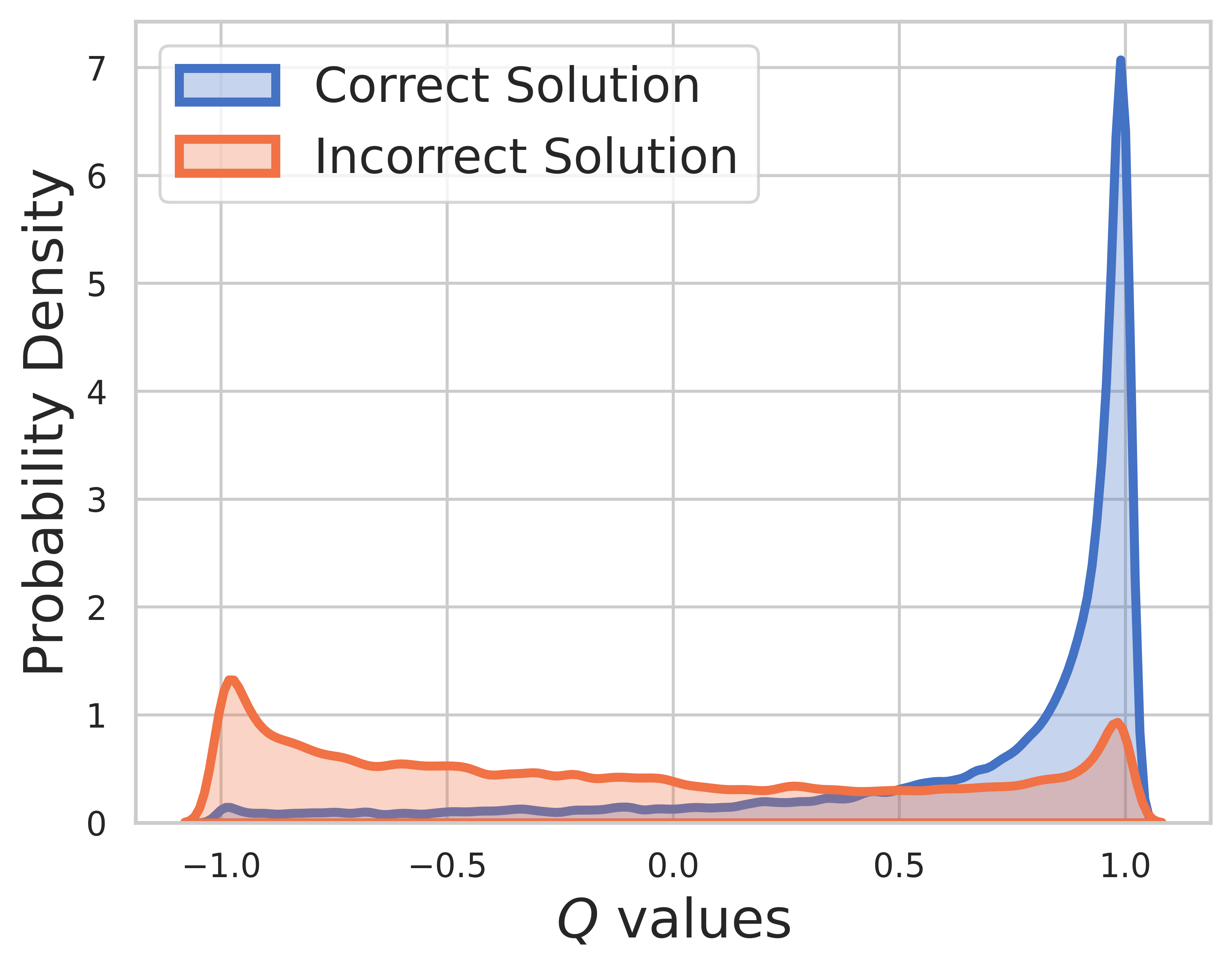
在测试集上，真实情况未知，因此 Q 值分布包括中间步骤和最终步骤。从这张图我们可以发现
MCTS 的 SVPO
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
MCTS版本
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
评估工具包
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
OVM（结果价值模型）版本
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}
