
这是 DSA.js 书的编码实现和 NPM 包的存储库。
在此存储库中,您可以找到 JavaScript 中算法和数据结构的实现。该材料可以用作开发人员的参考手册,也可以在面试前刷新特定主题。此外,您还可以找到更有效地解决问题的想法。
您可以克隆存储库或从 NPM 安装代码:
npm install dsa.js然后你可以将它导入到你的程序或 CLI 中
const { LinkedList , Queue , Stack } = require ( 'dsa.js' ) ;有关所有可用数据结构和算法的列表,请参阅index.js。
算法是每个程序员必不可少的工具箱。
当您必须对数据进行排序、在大数据集中搜索值、转换数据、将代码扩展到许多用户等时,您将需要注意算法运行时。算法只是解决问题所遵循的步骤,而数据结构是存储数据以供以后操作的地方。两者结合起来创建程序。
算法+数据结构=程序。
大多数编程语言和库确实提供了基本数据结构和算法的实现。然而,为了正确使用数据结构,您必须了解权衡以选择最适合工作的工具。
本材料将教您:
所有代码和解释都可以在此存储库中找到。您可以从(src 文件夹)中挖掘链接和代码示例。不过,内联代码示例并未展开(因为 Github 的 asciidoc 限制),但您可以按照路径查看实现。
注意:如果您喜欢更线性地使用信息,那么书籍格式会更适合您。
这些主题分为四个主要类别,如下所示:
计算机科学的金块没有任何繁琐的内容。 (点击展开)
计算机科学的金块,没有所有的繁文缛节
了解从代码示例计算运行时间
了解如何使用 Big O 表示法比较算法。 (点击展开)
了解如何使用 Big O 表示法比较算法。
使用 Big O 表示法比较算法
假设您想查找数组中的重复项。使用大 O 表示法,我们可以比较解决同一问题的不同解决方案,但在完成所需时间方面存在巨大差异。
- 使用地图的最佳解决方案
- 查找数组中的重复项(简单方法)
8个例子用代码解释如何计算时间复杂度。 (点击展开)
8个例子用代码解释如何计算时间复杂度
最常见的时间复杂度
时间复杂度图
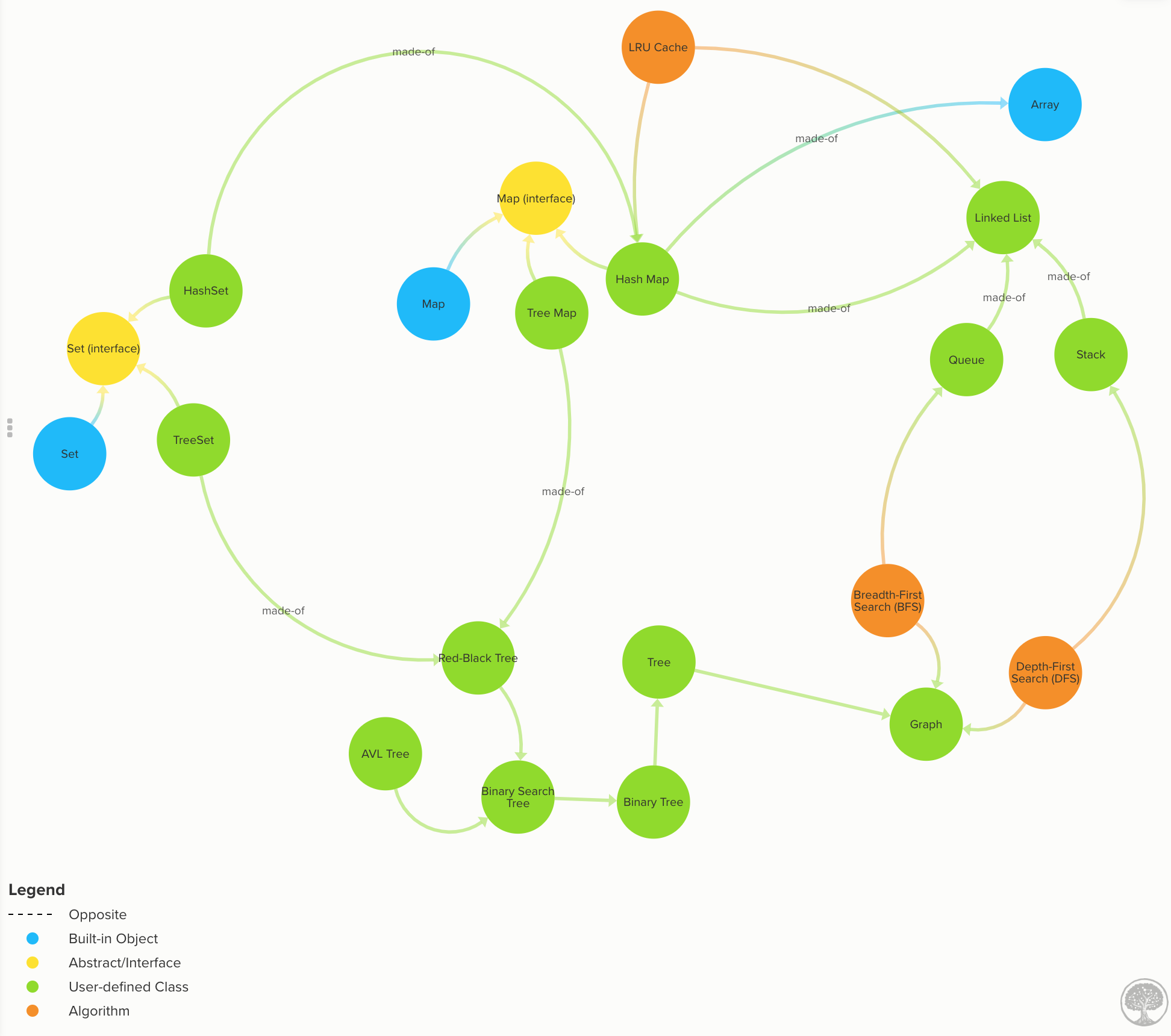
了解最常见数据结构的来龙去脉。 (点击展开)
了解最常见数据结构的来龙去脉
数组:在大多数语言中内置,因此此处未实现。数组时间复杂度
链表:每个数据节点都有一个到下一个(和上一个)的链接。代码|链表时间复杂度
队列:数据以“先进先出”(FIFO)方式流动。代码|队列时间复杂度
堆栈:数据以“后进先出”(LIFO)方式流动。代码|堆栈时间复杂度
何时使用数组或链表。了解权衡。 (点击展开)
何时使用数组或链表。了解权衡
当……时使用数组
- 您需要以随机顺序快速访问数据(使用索引)。
- 您的数据是多维的(例如矩阵、张量)。
在以下情况下使用链接列表:
- 您将按顺序访问您的数据。
- 您想要节省内存并仅在需要时分配内存。
- 您需要恒定的时间从列表的极端中删除/添加。
- 当尺寸要求未知时 - 动态尺寸优势
构建列表、堆栈和队列。 (点击展开)
从头开始构建列表、堆栈和队列
从头开始构建以下任何数据结构:
- 链表
- 堆
- 队列
了解最通用的数据结构之一:哈希图。 (点击展开)
哈希映射
了解如何实现不同类型的地图,例如:
- 哈希映射
- 树形图
另外,了解不同 Maps 实现之间的差异:
HashMap更省时。TreeMap更节省空间。TreeMap搜索复杂度为O(log n) ,而优化的HashMap平均为O(1) 。HashMap的键按插入顺序排列(或随机,具体取决于实现)。TreeMap的键始终是排序的。TreeMap免费提供一些统计数据,例如:获取最小值、获取最大值、中值、查找键范围。HashMap没有。TreeMap保证始终为O(log n) ,而HashMap的摊余时间为O(1) ,但在极少数情况下重新散列,则需要O(n) 。了解图和树的性质。 (点击展开)
了解图和树的属性
图表
通过大量图像和插图了解所有图形属性。
图:可以与零个或多个相邻节点有连接或边的数据节点。与树不同,节点可以有多个父节点、循环。代码|图时间复杂度
树木
了解所有不同种类的树木及其特性。
树:数据节点有零个或多个相邻节点(也称为子节点)。每个节点只能有一个父节点,否则是图,而不是树。代码|文档
二叉树:与树相同,但最多只能有两个孩子。代码|文档
二叉搜索树(BST):与二叉树相同,但节点值保持此顺序
left < parent < right。代码| BST 时间复杂度AVL 树:自平衡 BST 以最大化查找时间。代码| AVL 树文档 |自平衡和树旋转文档
红黑树:自平衡 BST 比 AVL 更宽松,以最大限度地提高插入速度。代码
实现二叉搜索树以进行快速查找。
实现二叉搜索树以进行快速查找
了解如何在树中添加/删除/更新值:
如何让树保持平衡?
从不平衡 BST 到平衡 BST
1 2 / 2 => 1 3 3
通过 7 个简单步骤解决问题,永远不会陷入困境。 (点击展开)
通过 8 个简单步骤解决问题,永远不会陷入困境
- 了解问题所在
- 构建一个简单的示例(尚无边缘情况)
- 集思广益解决方案(贪心算法、分而治之、回溯、暴力破解)
- 用简单的例子测试你的答案(心理上)
- 优化解决方案
- 写代码。是的,现在您可以编码了。
- 测试你编写的代码
- 分析空间和时间的复杂性,并确保进一步优化。
完整详细信息请参见此处
掌握最流行的排序算法(归并排序、快速排序等) (点击展开)
掌握最流行的排序算法
我们将探索三种基本的 O(n^2) 排序算法,它们具有较低的开销:
冒泡排序。代码|文档
插入排序。代码|文档
选择排序。代码|文档
然后讨论有效的排序算法 O(n log n) 例如:
归并排序。代码|文档
快速排序。代码|文档
学习解决问题的不同方法,例如分而治之、动态规划、贪心算法和回溯。 (点击展开)
学习解决算法问题的不同方法
我们将讨论以下解决算法问题的技术:
- 贪婪算法:使用启发式做出贪婪选择,以找到最佳解决方案而不回头。
- 动态规划:当存在许多重叠子问题时加速递归算法的技术。它使用记忆来避免重复工作。
- 分而治之:将问题分成更小的部分,解决每个子问题,然后连接结果。
- 回溯:搜索所有(或部分)可能的路径。但是,它会停止,并在发现当前解决方案不起作用后立即返回。
- 蛮力:生成所有可能的解决方案并尝试所有解决方案。 (将其用作最后的手段或作为起点)。
作为一名程序员,我们每天都要解决问题。如果您想很好地解决问题,最好了解各种解决方案。通常,学习现有资源比自己偶然找到答案更有效。您拥有的工具和练习越多越好。本书帮助您理解数据结构之间的权衡以及算法性能的原因。
关于 JavaScript 算法的书籍并不多。该材料填补了国内空白。另外,这是一个很好的做法:)
是的,在 [slack 频道](https://dsajs-slackin.herokuapp.com) 上提出问题或提出问题。
这个项目也可以在一本书中找到。您将获得一个格式精美的 PDF,包含 180 多页 + ePub 和 Mobi 版本。
请通过以下地点之一与我联系!
@iAmAdrianMejiadsajs.slack.com上聊天