常態分佈的 MLE - 實驗室

介紹

在本實驗中，我們將實踐我們在上一課中看到的數學公式，以了解 MLE 如何處理常態分佈。

目標

您將能夠：

理解並描述 MLE 如何與常態分佈一起工作
將常態分佈擬合到給定數據，識別平均值和方差
直觀比較擬合分佈與真實分佈

注意： *所有 MLE 方程式的詳細推導和證明可以在這個網站上看到。 *

Python 中的最大似然估計

下面讓我們來看一個使用 Python 進行 MLE 和分佈擬合的範例。這裡scipy.stats.norm.fit使用最大似然估計計算分佈參數。

導入必要的庫

 from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np

從平均值 0 和標準差 1 的常態分佈產生 200 個隨機樣本的陣列

 sample = None

透過 MLE 進行分佈擬合

- 使用`stats.norm.fit(data)`來擬合上述資料的分佈。

- 這會透過 MLE 方法傳回兩個參數的清單：(mean,:parameters[0] and std:parameters[1])

 param = None

#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)

根據 a) 實際資料參數 b) 擬合參數計算 PDF，其中`x = np.linspace(-5,5,100)`

 x = np . linspace ( - 5 , 5 , 100 )

# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None

可視化兩個 PDF

 # Your code here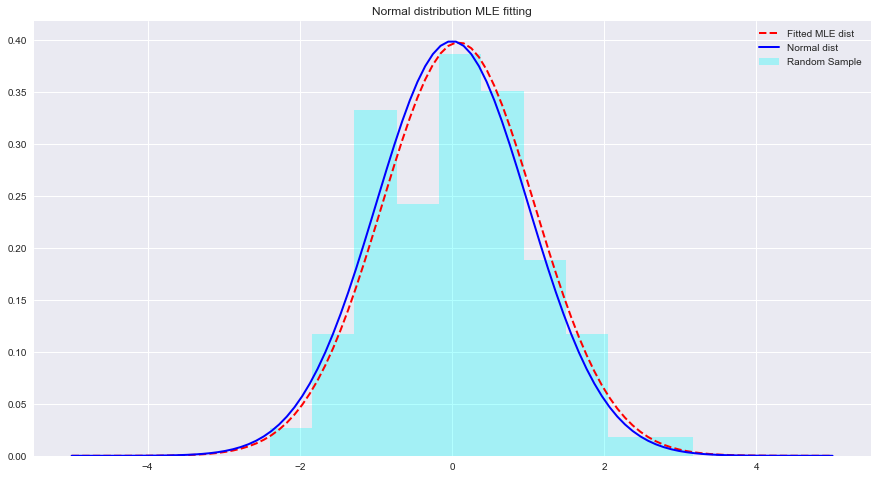

PNG

 #  Your comments/observations

概括

在這個簡短的實驗中，我們研究了高斯環境中的貝葉斯設置，即當基礎隨機變數呈常態分佈時。我們了解到，MLE 可以透過最大化預期平均值的可能性來估計常態分佈的未知參數。預期平均值非常接近該參數空間內非擬合常態分佈的平均值。我們將在這種理解的基礎上繼續學習如何使用樸素貝葉斯分類器來估計資料分佈中存在的許多類別的方法。

展開

附加信息