ai simplest network
1.0.0
這是可能解釋和演示的最簡單的人工神經網路。
人工神經網路受到大腦的啟發，透過互連的人工神經元儲存模式並相互溝通。最簡單形式的人工神經元有一個或多個輸入
每個都有特定的重量
和一個輸出
。
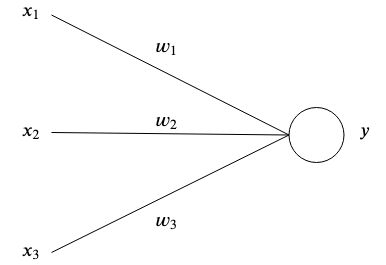
在最簡單的層面上，輸出是輸入的總和乘以權重。
網路的目的是學習特定的輸出給定某些輸入
透過近似具有許多參數的複雜函數
我們無法自己想出辦法。
假設我們有一個有兩個輸入的網絡
和
和兩個重量
和
。
這個想法是調整權重，使給定的輸入產生所需的輸出。
權重通常是隨機初始化的，因為我們無法事先知道它們的最佳值，但是為了簡單起見，我們將它們都初始化為
。
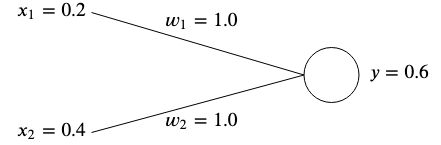
如果我們計算該網路的輸出，我們將得到
如果輸出與預期的目標值不匹配，那麼我們就會出錯。
例如，如果我們想要得到目標值
那我們會有差異
測量誤差（也稱為成本函數）的常見方法是使用均方誤差：
如果我們有輸入和目標值的多個關聯，那麼誤差就變成每個關聯的平均和。
我們使用均方誤差來衡量結果與我們期望目標的距離。平方消除了負號，並為輸出和目標之間的較大差異賦予更多權重。
為了修正錯誤，我們需要調整權重，使輸出與我們的目標相符。在我們的範例中，降低從
到
會成功的，因為
然而，為了針對許多不同的輸入和目標值調整神經網路的權重，我們需要一種學習演算法來自動為我們做到這一點。
這個想法是使用誤差來理解應該如何調整每個權重以使誤差最小化，但首先，我們需要了解梯度。
它本質上是一個指向函數最陡上升方向的向量。梯度表示為
是表示為向量的函數的每個變數的偏導數。
對於兩個變數函數來說，它看起來像這樣：
讓我們注入一些數字並用一個簡單的例子來計算梯度。假設我們有一個函數
，那麼梯度就是
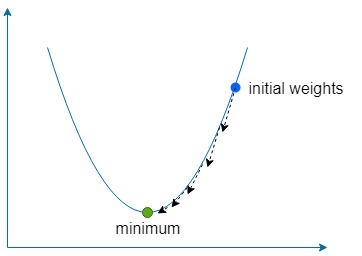
下降部分簡單地意味著使用梯度來找到函數最陡的上升方向，然後沿著相反方向多次移動以找到函數全局（有時是局部）最小值。
我們使用一個稱為學習率的常數，表示為
定義朝這個方向邁出多小的一步。
如果太大，那麼我們就有超過函數最小值的風險，但如果太低，那麼網路將需要更長的時間來學習，並且我們有陷入淺局部最小值的風險。
對於我們的兩個權重和我們需要找到這些權重相對於誤差函數的梯度
對於兩者和 ，我們可以利用鍊式法則求梯度
從現在開始我們將表示
作為
簡單的術語。
一旦我們有了梯度，我們就可以透過減去計算出的梯度乘以學習率來更新權重。
我們重複這個過程，直到誤差最小化並且足夠接近零。
包含的範例使用梯度下降向具有兩個輸入和一個輸出的神經網路教授以下資料集：
一旦學習到，當給定兩個時，網路應該輸出〜0 和〜 當給定一個和一個
。
docker build -t simplest-network .
docker run --rm simplest-network
