nano neuron

奈米神經元

7 個簡單的 JavaScript 函數將讓您了解機器如何真正「學習」。

其他語言：Русский、Português

您可能還感興趣？互動式機器學習實驗

長話短說

NanoNeuron 是神經網路中神經元概念的過度簡化版本。 NanoNeuron 經過訓練，可以將溫度值從攝氏度轉換為華氏度。

NanoNeuron.js 程式碼範例包含 7 個簡單的 JavaScript 函數（涉及模型預測、成本計算、前向/後向傳播和訓練），讓您了解機器如何實際「學習」。沒有第三方函式庫，沒有外部資料集或依賴項，只有純粹而簡單的 JavaScript 函數。

☝ ？許多機器學習概念被跳過並過度簡化！這種簡化的目的是讓讀者對機器如何學習有一個真正基本的理解和感受，並最終讓讀者認識到這不是“機器學習魔法”，而是“機器學習數學”？

我們的 NanoNeuron 將學到什麼

您可能聽說過神經網路背景下的神經元。 NanoNeuron 就是這樣，但更簡單，我們將從頭開始實現它。出於簡單原因，我們甚至不打算在 NanoNeurons 上建立網路。我們會讓這一切自行運作，為我們做出一些神奇的預測。也就是說，我們將教這個奇怪的 NanoNeuron 將溫度從攝氏度轉換（預測）為華氏度。

順便說一句，攝氏溫度轉換為華氏溫度的公式是這樣的：

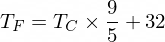
但目前我們的 NanoNeuron 還不知道...

奈米神經元模型

讓我們實作 NanoNeuron 模型函數。它實現了x和y之間的基本線性依賴關係，類似於y = w * x + b 。簡單地說，我們的 NanoNeuron 是“學校”中的一個“孩子”，正在被教導如何在XY座標中畫直線。

變數w 、 b是模型的參數。 NanoNeuron 只知道線性函數的這兩個參數。這些參數是 NanoNeuron 在訓練過程中要「學習」的東西。

NanoNeuron 唯一能做的就是模仿線性依賴。在它的predict()方法中，它接受一些輸入x並預測輸出y 。這裡沒有魔法。

 function NanoNeuron ( w , b ) {
  this . w = w ;
  this . b = b ;
  this . predict = ( x ) => {
    return x * this . w + this . b ;
  }
}

（...等等...線性迴歸是你嗎？） ？

攝氏 到 華氏 轉換

可使用下列公式將攝氏溫度值轉換為華氏溫度： f = 1.8 * c + 32 ，其中c是攝氏溫度， f是計算出的華氏溫度。

 function celsiusToFahrenheit ( c ) {
  const w = 1.8 ;
  const b = 32 ;
  const f = c * w + b ;
  return f ;
} ;

最終，我們希望教導我們的 NanoNeuron 模仿這個函數（學習w = 1.8和b = 32 ），而無需事先知道這些參數。

這是攝氏度到華氏度轉換函數的樣子：

產生資料集

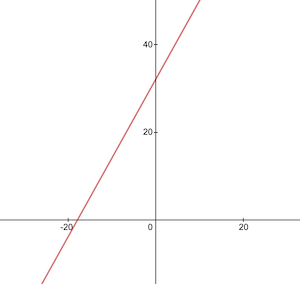
在訓練之前，我們需要根據celsiusToFahrenheit()函數產生訓練和測試資料集。資料集由成對的輸入值和正確標記的輸出值組成。

在現實生活中，在大多數情況下，這些數據是被收集而不是產生的。例如，我們可能有一組手繪數位影像以及相應的一組數字，用於解釋每張圖片上寫的數字。

我們將使用 TRAINING 範例資料來訓練我們的 NanoNeuron。在我們的 NanoNeuron 成長並能夠自行做出決策之前，我們需要使用訓練範例來教它什麼是對的，什麼是錯的。

我們將使用測試範例來評估我們的 NanoNeuron 在訓練期間未看到的資料上的表現如何。這時我們可以看到我們的「孩子」已經長大並且可以自己做決定了。

 function generateDataSets ( ) {
  // xTrain -> [0, 1, 2, ...],
  // yTrain -> [32, 33.8, 35.6, ...]
  const xTrain = [ ] ;
  const yTrain = [ ] ;
  for ( let x = 0 ; x < 100 ; x += 1 ) {
    const y = celsiusToFahrenheit ( x ) ;
    xTrain . push ( x ) ;
    yTrain . push ( y ) ;
  }

  // xTest -> [0.5, 1.5, 2.5, ...]
  // yTest -> [32.9, 34.7, 36.5, ...]
  const xTest = [ ] ;
  const yTest = [ ] ;
  // By starting from 0.5 and using the same step of 1 as we have used for training set
  // we make sure that test set has different data comparing to training set.
  for ( let x = 0.5 ; x < 100 ; x += 1 ) {
    const y = celsiusToFahrenheit ( x ) ;
    xTest . push ( x ) ;
    yTest . push ( y ) ;
  }

  return [ xTrain , yTrain , xTest , yTest ] ;
}

預測的成本（誤差）

我們需要一些指標來顯示模型的預測與正確值的接近程度。將使用以下公式計算y的正確輸出值與我們的 NanoNeuron 建立的prediction之間的成本（錯誤）：

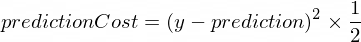
這是兩個值之間的簡單差異。值彼此越接近，差異越小。我們在這裡使用2的冪只是為了消除負數，以便(1 - 2) ^ 2與(2 - 1) ^ 2相同。除以2只是為了進一步簡化反向傳播公式（見下文）。

在這種情況下，成本函數將非常簡單：

 function predictionCost ( y , prediction ) {
  return ( y - prediction ) ** 2 / 2 ; // i.e. -> 235.6
}

前向傳播

進行前向傳播意味著對xTrain和yTrain資料集中的所有訓練範例進行預測，並計算這些預測的平均成本。

此時，我們只是讓 NanoNeuron 說出它的意見，只允許它猜測如何轉換溫度。這裡可能是愚蠢的錯誤。平均成本將告訴我們我們的模型現在有多錯誤。這個成本值非常重要，因為更改 NanoNeuron 參數w和b並再次進行前向傳播；我們將能夠評估這些參數改變後我們的 NanoNeuron 是否變得更聰明。

平均成本將使用以下公式計算：

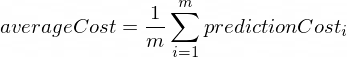
其中m是訓練範例的數量（在我們的例子中： 100 ）。

下面是我們如何在程式碼中實現它：

 function forwardPropagation ( model , xTrain , yTrain ) {
  const m = xTrain . length ;
  const predictions = [ ] ;
  let cost = 0 ;
  for ( let i = 0 ; i < m ; i += 1 ) {
    const prediction = nanoNeuron . predict ( xTrain [ i ] ) ;
    cost += predictionCost ( yTrain [ i ] , prediction ) ;
    predictions . push ( prediction ) ;
  }
  // We are interested in average cost.
  cost /= m ;
  return [ predictions , cost ] ;
}

向後傳播

當我們知道 NanoNeuron 的預測有多正確或錯誤時（基於此時的平均成本），我們應該做什麼來使預測更加精確？

反向傳播給了我們這個問題的答案。反向傳播是評估預測成本並調整 NanoNeuron 參數w和b的過程，以便下一個和未來的預測更加精確。

這就是機器學習看起來神奇的地方？這裡的關鍵概念是導數，它顯示了要採取什麼步驟來接近成本函數最小值。

請記住，找到成本函數的最小值是訓練過程的最終目標。如果我們發現w和b值使得我們的平均成本函數很小，則表示 NanoNeuron 模型確實可以做出很好且精確的預測。

衍生性商品是一個大而獨立的主題，我們不會在本文中討論。 MathIsFun 是一個很好的資源，可以幫助您基本上了解它。

關於導數的一件事將幫助您理解反向傳播的工作原理，那就是導數，就其含義而言，是函數曲線的一條切線，指向函數最小值的方向。

圖片來源：MathIsFun

例如，在上圖中，您可以看到，如果我們位於(x=2, y=4)點，那麼斜率會告訴我們left和down移動以達到函數最小值。另請注意，斜率越大，我們移動到最小值的速度就越快。

參數w和b的averageCost函數的導數如下：

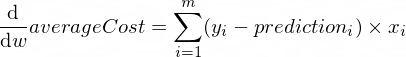
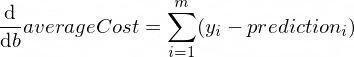
其中m是訓練範例的數量（在我們的例子中： 100 ）。

您可以在此處閱讀有關導數規則以及如何獲得複雜函數的導數的更多資訊。

 function backwardPropagation ( predictions , xTrain , yTrain ) {
  const m = xTrain . length ;
  // At the beginning we don't know in which way our parameters 'w' and 'b' need to be changed.
  // Therefore we're setting up the changing steps for each parameters to 0.
  let dW = 0 ;
  let dB = 0 ;
  for ( let i = 0 ; i < m ; i += 1 ) {
    dW += ( yTrain [ i ] - predictions [ i ] ) * xTrain [ i ] ;
    dB += yTrain [ i ] - predictions [ i ] ;
  }
  // We're interested in average deltas for each params.
  dW /= m ;
  dB /= m ;
  return [ dW , dB ] ;
}

訓練模型

現在我們知道如何評估所有訓練集範例的模型的正確性（前向傳播）。我們也知道如何對 NanoNeuron 模型的參數w和b進行小調整（反向傳播）。但問題是，如果我們只運行一次前向傳播，然後再運行一次反向傳播，我們的模型不足以從訓練資料中學習任何規律/趨勢。您可以將其與孩子上一天小學進行比較。他/她不應該去學校一次，而是日復一日、年復一年地去學習一些東西。

所以我們需要多次重複我們的模型的前向和後向傳播。這正是trainModel()函數的作用。它就像我們 NanoNeuron 模型的「老師」：

• 它將花費一些時間（ epochs ）來處理我們有點愚蠢的 NanoNeuron 模型，並嘗試訓練/教導它，
• 它將使用特定的“書籍”（ xTrain和yTrain資料集）進行訓練，
• 它將透過使用學習率參數alpha促使我們的孩子更加努力（更快）地學習

關於學習率alpha幾句話。這只是我們在反向傳播過程中計算出的dW和dB值的乘數。因此，導數為我們指明了尋找成本函數最小值（ dW和dB符號）所需的方向，也向我們展示了朝該方向需要多快的速度（ dW和dB的絕對值）。現在我們需要將這些步長乘以alpha以將我們的移動速度調整到最小值，更快或更慢。有時，如果我們對alpha使用較大的值，我們可能會簡單地跳過最小值而永遠找不到它。

與老師的類比是，他/她越用力地逼我們的“納米孩子”，我們的“納米孩子”學得就越快，但如果老師逼得太緊，“孩子”就會精神崩潰並獲勝。學不到任何東西？

以下是我們如何更新模型的w和b參數：

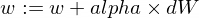
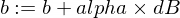
這是我們的訓練器函數：

 function trainModel ( { model , epochs , alpha , xTrain , yTrain } ) {
  // The is the history array of how NanoNeuron learns.
  const costHistory = [ ] ;

  // Let's start counting epochs.
  for ( let epoch = 0 ; epoch < epochs ; epoch += 1 ) {
    // Forward propagation.
    const [ predictions , cost ] = forwardPropagation ( model , xTrain , yTrain ) ;
    costHistory . push ( cost ) ;
  
    // Backward propagation.
    const [ dW , dB ] = backwardPropagation ( predictions , xTrain , yTrain ) ;
  
    // Adjust our NanoNeuron parameters to increase accuracy of our model predictions.
    nanoNeuron . w += alpha * dW ;
    nanoNeuron . b += alpha * dB ;
  }

  return costHistory ;
}

把所有的部分放在一起

現在讓我們使用上面創建的函數。

讓我們建立 NanoNeuron 模型實例。此時 NanoNeuron 不知道應該為參數w和b設定什麼值。所以讓我們隨機設定w和b 。

 const w = Math . random ( ) ; // i.e. -> 0.9492
const b = Math . random ( ) ; // i.e. -> 0.4570
const nanoNeuron = new NanoNeuron ( w , b ) ;

產生訓練和測試資料集。

 const [ xTrain , yTrain , xTest , yTest ] = generateDataSets ( ) ;

讓我們以小增量 ( 0.0005 ) 步長訓練模型70000個週期。您可以使用這些參數，它們是根據經驗定義的。

 const epochs = 70000 ;
const alpha = 0.0005 ;
const trainingCostHistory = trainModel ( { model : nanoNeuron , epochs , alpha , xTrain , yTrain } ) ;

讓我們檢查一下成本函數在訓練期間如何變化。我們預計培訓後的成本會比之前低很多。這意味著 NanoNeuron 變得更聰明。相反的情況也是可能的。

 console . log ( 'Cost before the training:' , trainingCostHistory [ 0 ] ) ; // i.e. -> 4694.3335043
console . log ( 'Cost after the training:' , trainingCostHistory [ epochs - 1 ] ) ; // i.e. -> 0.0000024

這就是訓練成本隨時代的變化的情況。 x軸上是紀元號 x1000。

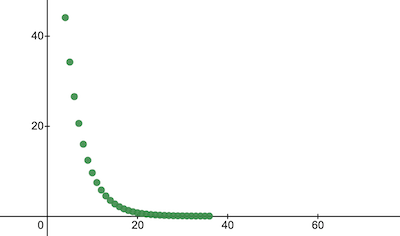
讓我們來看看 NanoNeuron 參數，看看它學到了什麼。我們預期 NanoNeuron 參數w和b與celsiusToFahrenheit()函數中的參數相似（ w = 1.8和b = 32 ），因為我們的 NanoNeuron 試圖模仿它。

 console . log ( 'NanoNeuron parameters:' , { w : nanoNeuron . w , b : nanoNeuron . b } ) ; // i.e. -> {w: 1.8, b: 31.99}

評估測試資料集的模型準確性，看看我們的 NanoNeuron 處理新的未知資料預測的效果如何。測試集預測的成本預計將接近訓練成本。這意味著我們的 NanoNeuron 在已知和未知數據上表現良好。

 [ testPredictions , testCost ] = forwardPropagation ( nanoNeuron , xTest , yTest ) ;
console . log ( 'Cost on new testing data:' , testCost ) ; // i.e. -> 0.0000023

現在，由於我們看到我們的NanoNeuron“孩子”在訓練期間在“學校”表現良好，並且他可以正確地將攝氏溫度轉換為華氏溫度，即使對於它沒有見過的數據，我們可以稱其為“聰明」並問他一些問題。這是整個訓練過程的最終目標。

 const tempInCelsius = 70 ;
const customPrediction = nanoNeuron . predict ( tempInCelsius ) ;
console . log ( `NanoNeuron "thinks" that ${ tempInCelsius } °C in Fahrenheit is:` , customPrediction ) ; // -> 158.0002
console . log ( 'Correct answer is:' , celsiusToFahrenheit ( tempInCelsius ) ) ; // -> 158

這麼近！與我們所有人一樣，我們的 NanoNeuron 很好，但並不理想:)

祝你學習愉快！

如何啟動 NanoNeuron

您可以克隆存儲庫並在本地運行它：

git clone https://github.com/trekhleb/nano-neuron.git
cd nano-neuron

node ./NanoNeuron.js

跳過機器學習概念

為了簡化解釋，跳過並簡化了以下機器學習概念。

訓練/測試資料集分割

通常你有一大組數據。根據該集中的範例數量，您可能想要以 70/30 的比例將其拆分為訓練/測試集。集合中的資料應該在分割之前隨機打亂。如果範例數量很大（即數百萬），則訓練/測試資料集的分割比例可能接近 90/10 或 95/5。

網路帶來力量

通常您不會注意到僅使用一個獨立神經元。力量就在於這些神經元的網路。網路可能會學習更複雜的特徵。 NanoNeuron 本身看起來更像是一個簡單的線性迴歸，而不是神經網路。

輸入標準化

在訓練之前，最好先對輸入值進行標準化。

向量化實現

對於網絡，向量化（矩陣）計算比for迴圈快得多。通常，如果以向量化形式實現並使用 Numpy Python 庫等進行計算，則前向/後向傳播的工作速度會更快。

成本函數的最小值

我們在本例中使用的成本函數過於簡化。它應該具有對數分量。更改成本函數也會更改其導數，因此反向傳播步驟也會使用不同的公式。

激活函數

通常，神經元的輸出應該透過 Sigmoid 或 ReLU 等活化函數傳遞。

作者

• @trekhleb