
React中的Fiber任務都應該知道吧,而且不同的Fiber任務有不同的優先級,React需要先處理優先順序高的任務。例如,使用者的點擊和輸入,這些都是高優先級的任務,因為使用者的操作肯定希望馬上就會有效果,這樣才能提升使用者體驗。而例如animation事件的優先順序肯定要低一點。新進來的高優先權任務進去佇列後,React需要優先處理。
為了儲存這些任務,React中有兩個任務池。
// Tasks are stored on a min heap var taskQueue = []; var timerQueue = [];
taskQueue與timerQueue都是數組,前者儲存的是立即要執行的任務,而後者存的則是可以延遲執行的任務。
var newTask = {
id: taskIdCounter++, // 標記任務id
callback, // 回呼函數priorityLevel, // 任務優先權startTime, // 任務開始時間,時間點expirationTime, // 過期時間,時間點sortIndex: -1, // 任務排序,取值來自過期時間,因此值越小,優先權越高}; React中一旦來了新任務,就會先用currentTime記錄當前時間(performance.now()或Date.now()),如果任務有delay參數,那麼任務開始執行時間startTime = currentTime + delay;。接下來透過startTime > currentTime如果成立,證明任務是可以延期的,那麼任務進入timerQueue,否則進入taskQueue。
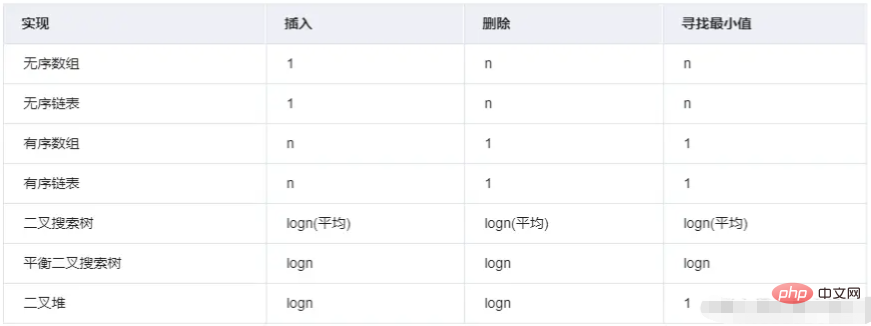
React怎麼找到優先權最高的任務呢,以taskQueue為例,它是動態的任務池(任務佇列),資料形式上就是一個陣列。當然可以依照優先順序排序,也就是Array.sort,當有新任務入隊後,先排序,再找出優先順序最高的任務執行。但是Array.sort的平均時間複雜度是O(nlogn),並不是最好的解決方案。
taskQueue的newTask中排序用的是sortIndex,這個值取自過期時間expirationTime,也就意味著優先權越高的任務越需要理解執行,那麼過期時間就越小,也就是說,優先權越高,過期時間越小,sortIndex自然越小。其實,這就是一種優先隊列。
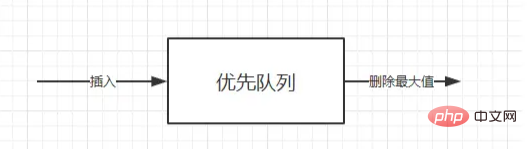
優先隊列也是一種隊列(首先它是一個隊列,其次是尾進頭出),只不過不同的是,優先隊列的出隊順序是按照優先權來的;在某些情況下,可能需要找到元素集合中的最小或最大元素,可以利用優先隊列ADT來完成操作,優先隊列ADT是一種資料結構,它支援插入和刪除最小值操作(返回並刪除最小元素)或刪除最大值操作(返回並刪除最大元素)。
如果最小鍵值元素擁有最高的優先權,那麼這個優先權佇列叫做,升序優先權佇列(即總是先刪除最小的元素)。類似的,如果最大鍵值元素擁有最高的優先權,那麼這種優先權佇列叫作降序優先權佇列(即總是先刪除最大的元素);由於這兩種類型時對稱的,所以只需要關注其中一種,如昇序優先隊列。
例如:買車票的時候,我們都在排隊,優先級是一樣的,誰在隊伍前面,誰就先買票,但是這時候來了個軍人,他的優先級高,直接就排在了隊伍的最前面。
在React中用最小堆(小根堆,小頂堆。。。)來實現這種功能。就是把taskQueue變成最小堆,然後取出對頂任務執行,對taskQueue堆化,維持它依然是一個最小堆的資料結構。往taskQueue插入新任務的時候,也要進行堆化,始終保持它是一個最小堆。
有些地方稱堆為優先隊列(不準確),首先它是隊列,有隊列的特性,也就是「先進先出」。其次這個佇列中的元素是有優先權的,優先權高的會排在前面。
準確來說,堆是實現優先隊列的一種方式。當然優先隊列還可以用其他方式來實現。
之前我們說過堆排序是不穩定排序,但taskQueue希望這個過程是穩定的,也就是說,如果有可能兩個任務的過期時間一樣,那這個時候就要看誰先進入的任務池了,也就是newTask的id的值,每次來了新任務,id都會加1。
function compare(a, b) {
// Compare sort index first, then task id.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
}在了解最小堆之前,先來溫習一下基礎知識。
是指樹中節點的度數不大於2的有序樹,它是一種最簡單且最重要的樹。
除最後一層無任何子節點外,每一層上的所有結點都有兩個子結點的二元樹。
從圖形形狀上看,滿二叉樹外觀上是一個三角形。
如果一個二元樹的層數為K,且結點總數是(2^k) -1 ,則它就是滿二元樹。
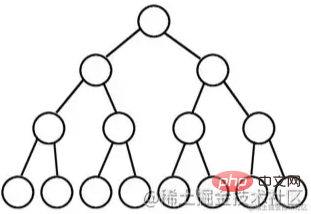
滿二元樹,是“女兒雙全”,非常圓滿,所以叫滿二叉樹。
除去葉子節點, 所有節點的度都是2。也就是說,所有的節點的度數只能是0或2。
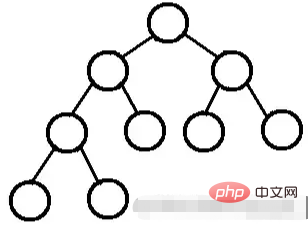
完美二元樹,要嘛沒有孩子,要嘛兒女雙全。
滿二元樹的英文原文:
A Full Binary Tree (FBT) is a tree in which every node other than the leaves has two children.
完美二叉樹的英文原文:
A Perfect Binary Tree(PBT) is a tree with all leaf nodes at the same depth. All internal nodes have degree 2.
國外的所有書籍參考的是最早翻譯的關於滿二叉樹,和完美二元樹的教材,但是最早翻譯的文章翻譯錯了。現在國內的話,我們只能將錯就錯了(所有人都錯,那錯的也就是對的了。比如說客。。。)。如果要和外國友人討論這兩個概念,就要注意了。
二元樹A Complete Binary Tree (CBT) is a binary tree in which every level,except possibly the last, is completely filled, and all nodes are as far left as possible.
一棵深度為k的有n個結點的二叉樹,將樹中的結點按從上至下、從左到右的順序進行編號,如果編號為i(1≤i≤n)的結點與滿二叉樹中編號為i的結點在二叉樹中的位置相同,則這棵二元樹稱為完全二元樹。
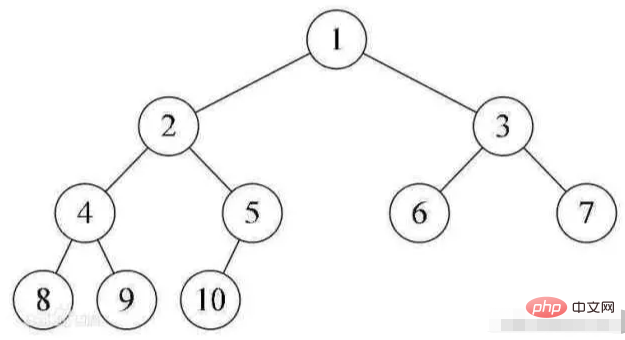
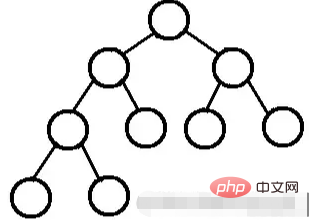
堆總是滿足下列性質:
還要先認識下大根堆和小根堆,完全二叉樹中所有節點均大於(或小於)它的孩子節點,所以這裡就分為兩種情況,最大堆和最小堆。
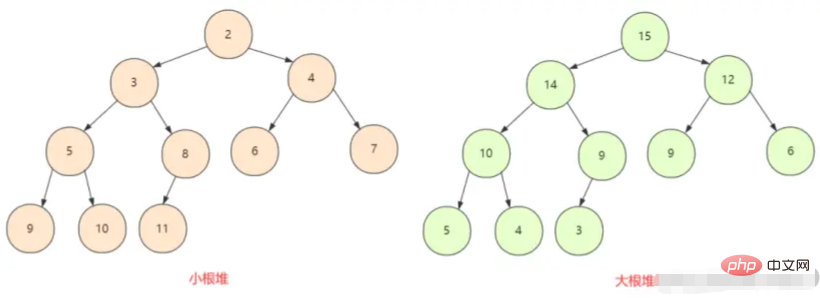
堆通常是一個可以被看做一棵完全二元樹的陣列物件。當然,二元樹也可以用陣列表示。
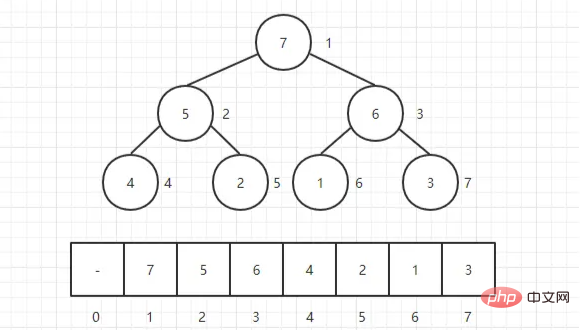
核心思想是,先建堆,後再調整。
對於二元樹(數組表示),我們從下往上進行調整,從**“第一個非葉子節點”**開始向前調整,對於調整的規則如下:
建堆是一個O(n)的時間複雜度過程。
①從第一個非葉子節點開始判斷交換下移(shiftDown),使得當前節點和子孩子能夠保持堆的性質
②但是普通節點替換可能沒問題,對如果交換打破子孩子堆結構性質,那麼就要重新下移(shiftDown)被交換的節點一直到停止。
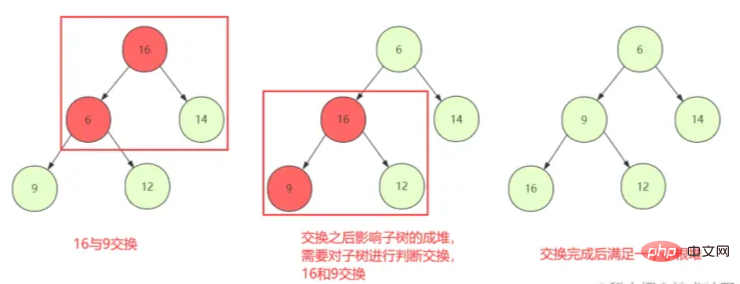
堆堆
破壞堆結構。
① 所以索性把最後一個元素放到第一位。這樣只需要判斷交換下移(shiftDown),不過需要注意此時整個堆的大小已經發生了變化,我們在邏輯上不會使用被拋棄的位置,所以在設計函數的時候需要附帶一個堆大小的參數。
② 重複以上操作,一直堆中所有元素都被取得停止。
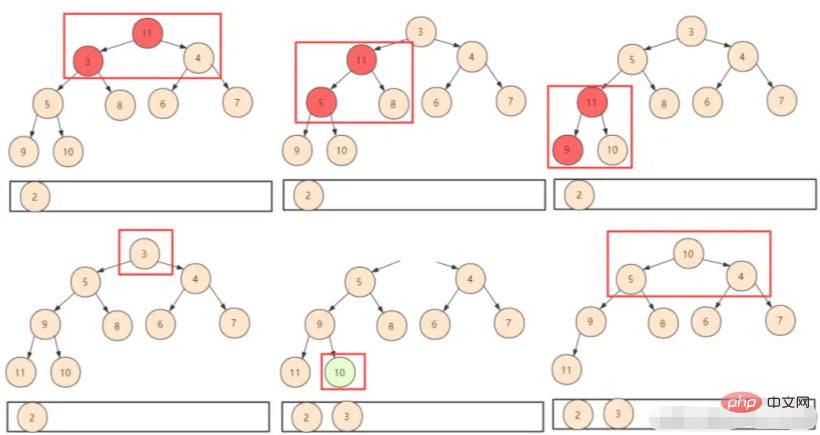
在而堆演算法複雜度的分析上,之前建堆時間複雜度是O(n)。而每次刪除堆頂然後需要向下交換,每個個數為logn個。這樣複雜度就為O(nlogn),總的時間複雜度為O(n)+O(nlogn)=O(nlogn)。
堆適合維護集合的最值。
堆pop出一個元素後,再次調整取得堆頂元素(也就是第二個最值)的花銷比較低,因為pop出元素後,堆是一個半成品,在一個半成品上取得第二個最值的cost當然比較低,時間複雜度為O(logn),但若遍歷一遍找到第二個最值的話,時間複雜度為O(n)。
採用Javascript ES6的寫法。
class Heap {
constructor(data, comp) {
this.data = data ? data : [];
// 比較規則:更靈活,可以比較數值,也可以比較物件this.compartor = comp ? comp : (ab) => ab;
// 調整為堆疊(優先隊列)
this.heapify();
}
heapify() {
if(this.size() <= 1) return;
// 從第一個非葉子節點開始調整,也可以從最後一個元素開始調整for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
// 調整堆, 向下調整也可以用遞歸來實現,這裡用迭代來實現this.shiftDown(i);
}
}
// 向下調整shiftDown(i) {
let left = 2*i +1;
let right = 2*i +2;
let len = this.size();
while(i < len) {
let findIndex = i;
// 左孩子更“大”
if(left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
findIndex = left;
}
// 右孩子更“大”
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = right;
}
if(i !== findIndex) {
// 目前節點與更「大」的值交換[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// 調整完本層,可能會影響下層的堆的特性,所以要繼續調整下層(迭代實現,也可以遞歸)
i = findIndex;
left = 2*i +1;
right = 2*i +2;
}
else {
// 如果無需調整,則跳出(必須跳出,否則循環無法結束)
break;
}
}
}
// 向上調整shiftUp(i){
// 找到parent的下標let parentIndex = Math.floor((i-1)/2);
// 最高調整到0
while(parentIndex >=0 ) {
let findIndex = i;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = parentIndex;
}
if(findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = findIndex;
parentIndex = Math.floor((i-1)/2);
}
else {
break;
}
}
}
// 取得堆中所有元素的個數size(){
return this.data.length;
}
// 取得堆首部元素peek(){
if(!this.size()) return null;
return this.data[0];
}
// 在堆中加入一個元素push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// 從堆中彈出堆首元素pop(){
if(!this.size()) return null;
let res = this.data[0];
if(this.size() == 1) {
this.data.pop();
}
else {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
this.shiftDown(0);
}
return res;
}
}let arr = [2,9,8,6,3,10,5,7,4,1];
let comp = (a, b) => ab;
let heap = new Heap(arr, comp);
let res = [];
while(heap.size()) {
res.push(heap.pop());
}
console.log(res); arr裡的元素也可以是一個物件。
React原始碼中的目錄packages/scheduler,就是React的任務調度模組相關的程式碼。
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* Copyright (c) Facebook, Inc. and its affiliates.
*
* This source code is licensed under the MIT license found in the
* LICENSE file in the root directory of this source tree.
*
* @flow strict
*/
type Heap = Array<Node>;
type Node = {|
id: number,
sortIndex: number,
|};
export function push(heap: Heap, node: Node): void {
const index = heap.length;
heap.push(node);
siftUp(heap, node, index);
}
export function peek(heap: Heap): Node | null {
const first = heap[0];
return first === undefined ? null : first;
}
export function pop(heap: Heap): Node | null {
const first = heap[0];
if (first !== undefined) {
const last = heap.pop();
if (last !== first) {
heap[0] = last;
siftDown(heap, last, 0);
}
return first;
} else {
return null;
}
}
function siftUp(heap, node, i) {
let index = i;
while (true) {
const parentIndex = (index - 1) >>> 1;
const parent = heap[parentIndex];
if (parent !== undefined && compare(parent, node) > 0) {
// The parent is larger. Swap positions.
heap[parentIndex] = node;
heap[index] = parent;
index = parentIndex;
} else {
// The parent is smaller. Exit.
return;
}
}
}
function siftDown(heap, node, i) {
let index = i;
const length = heap.length;
while (index < length) {
const leftIndex = (index + 1) * 2 - 1;
const left = heap[leftIndex];
const rightIndex = leftIndex + 1;
const right = heap[rightIndex];
// If the left or right node is smaller, swap with the smaller of those.
if (left !== undefined && compare(left, node) < 0) {
if (right !== undefined && compare(right, left) < 0) {
heap[index] = right;
heap[rightIndex] = node;
index = rightIndex;
} else {
heap[index] = left;
heap[leftIndex] = node;
index = leftIndex;
}
} else if (right !== undefined && compare(right, node) < 0) {
heap[index] = right;
heap[rightIndex] = node;
index = rightIndex;
} else {
// Neither child is smaller. Exit.
return;
}
}
}
function compare(a, b) {
// Compare sort index first, then task id.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
}我們自己實作的最小堆和React中的實作略有不同,但是思路是一樣的,只是程式碼寫法不同而已。
React中的任務調度是用最小堆來實現的,如果我們之前就對最小堆有一定了解,那在學習這塊內容的時候就會更快一點。個人認為,前期知識累積是多麼重要啊,但是這個過程可能會比較枯燥。 這時候,是不是覺得自己也會一些演算法了,其實這些演算法是入門級的,甚至還沒有入門。因為在React的任務調度場景中,要實現的需求是非常明確的,而且要採用什麼樣的資料結構和演算法也是明確的。在實際的一些場景中,我們知道了具體的需求,但是我們不知道用什麼資料結果和演算法,就需要把需求抽像一下,根據抽象的資料模型來設計具體的資料結構和演算法,這些才是重點。