في هذا المختبر، سوف نطبق الصيغ الرياضية التي رأيناها في الدرس السابق لنرى كيف يعمل MLE مع التوزيعات العادية.
سوف تكون قادرا على:
ملحوظة: * يمكن الاطلاع على الاشتقاق التفصيلي لجميع معادلات MLE مع البراهين على هذا الموقع. *
دعونا نرى مثالاً على MLE وتجهيزات التوزيع مع Python أدناه. هنا، يقوم scipy.stats.norm.fit بحساب معلمات التوزيع باستخدام تقدير الاحتمال الأقصى.
from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np sample = Nonestats.norm.fit(data) لملاءمة التوزيع للبيانات المذكورة أعلاه. param = None
#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)x = np.linspace(-5,5,100) x = np . linspace ( - 5 , 5 , 100 )
# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None # Your code here 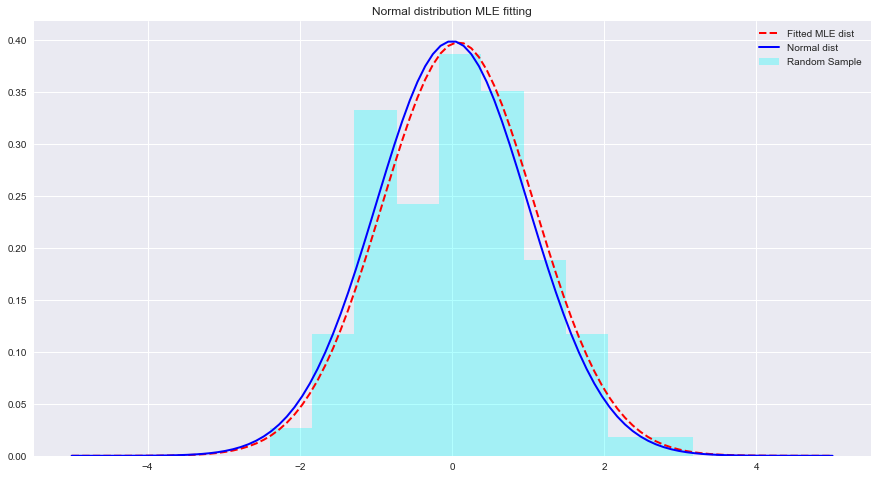
# Your comments/observations في هذا المختبر القصير، نظرنا إلى الإعداد البايزي في سياق غاوسي، أي عندما يتم توزيع المتغيرات العشوائية الأساسية بشكل طبيعي. لقد تعلمنا أن MLE يمكنه تقدير المعلمات غير المعروفة للتوزيع الطبيعي، من خلال تعظيم احتمالية المتوسط المتوقع. يقترب المتوسط المتوقع جدًا من متوسط التوزيع الطبيعي غير المناسب ضمن مساحة المعلمة تلك. سنمضي قدمًا في هذا الفهم نحو تعلم كيفية إجراء هذه التقديرات في تقدير وسائل عدد من الفئات الموجودة في توزيع البيانات باستخدام Naive Bayes Classifier.