

Le package FRK est disponible sur CRAN ! Pour installer, veuillez taper
install.packages( " FRK " ) Pour installer la version de développement la plus récente, veuillez charger devtools et taper
install_github( " andrewzm/FRK " , dependencies = TRUE , build_vignettes = TRUE )Un article présentant le package est disponible ici. Un article détaillant l'approche dans un cadre non gaussien est disponible ici (un résumé de six pages de cet article est disponible ici).
La vignette "FRK_intro" résume le package, donne des détails sur l'algorithme EM qui peut être utilisé dans un cadre gaussien et fournit plusieurs exemples. Une autre vignette, "FRK_non-Gaussian", résume l'inférence dans un contexte non gaussien (où une approximation de Laplace est utilisée) et contient des exemples utilisant des données non gaussiennes et les nouvelles méthodes de traçage disponibles. Pour accéder aux vignettes, veuillez cliquer sur les liens suivants :
Introduction à FRK
Tutoriel sur la modélisation de données spatiales et spatio-temporelles non-gaussiennes avec FRK
Une page pkgdown est également disponible ici.
Si vous utilisez FRK dans votre travail, vos recherches ou d'autres activités, veuillez le citer en utilisant les informations fournies par citation("FRK") .
Paquet: FRK
Type: Paquet
Titre : Krigeage à rang fixe
Version : 2.3.1
Dates : 2024-07-16
Auteurs : Andrew Zammit-Mangion, Matthew Sainsbury-Dale
Responsable : Andrew Zammit-Mangion [email protected]
Description : Un outil de modélisation et de prédiction spatiales/spatio-temporelles avec de grands ensembles de données. L'approche modélise le champ, et donc la fonction de covariance, à l'aide d'un ensemble de fonctions de base. Cette représentation de fonction de base de rang fixe facilite la modélisation du Big Data et la méthode permet naturellement des fonctions de covariance anisotropes non stationnaires. La discrétisation du domaine spatial en unités dites de base (BAU) facilite l'utilisation d'observations avec des supports variables (c'est-à-dire des supports à la fois référencés et surfaciques, potentiellement simultanément) et la prédiction sur des régions arbitraires spécifiées par l'utilisateur. FRK prend également en charge l'inférence sur diverses variétés, notamment le plan 2D et la sphère 3D, et fournit des fonctions d'assistance pour modéliser, ajuster, prédire et tracer avec une relative facilité. La version 2.0.0 et supérieure prend également en charge la modélisation de données non gaussiennes (par exemple, Poisson, binomiale, binomiale négative, gamma et gaussienne inverse) en employant un cadre de modèle mixte linéaire généralisé (GLMM). Zammit-Mangion et Cressie (2021) décrivent FRK dans un cadre gaussien et détaillent son utilisation des fonctions de base et des BAU, tandis que Sainsbury-Dale et al. (2024) décrivent FRK dans un contexte non gaussien ; deux vignettes sont disponibles qui résument ces articles et fournissent des exemples supplémentaires.
Licence : GPL (>= 2)
library( " FRK " )
library( " sp " )
library( " ggplot2 " )
library( " ggpubr " )
# # Setup
m <- 1000 # Sample size
RNGversion( " 3.6.0 " ); set.seed( 1 ) # Fix seed
zdf <- data.frame ( x = runif( m ), y = runif( m )) # Generate random locs
zdf $ z <- sin( 8 * zdf $ x ) + cos( 8 * zdf $ y ) + 0.5 * rnorm( m ) # Simulate data
coordinates( zdf ) = ~ x + y # Turn into sp object
# # Run FRK
S <- FRK( f = z ~ 1 , # Formula to FRK
list ( zdf ), # All datasets are supplied in list
n_EM = 10 ) # Max number of EM iterations
pred <- predict( S ) # Prediction stage
# # Plotting
plotlist <- plot( S , pred )
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )
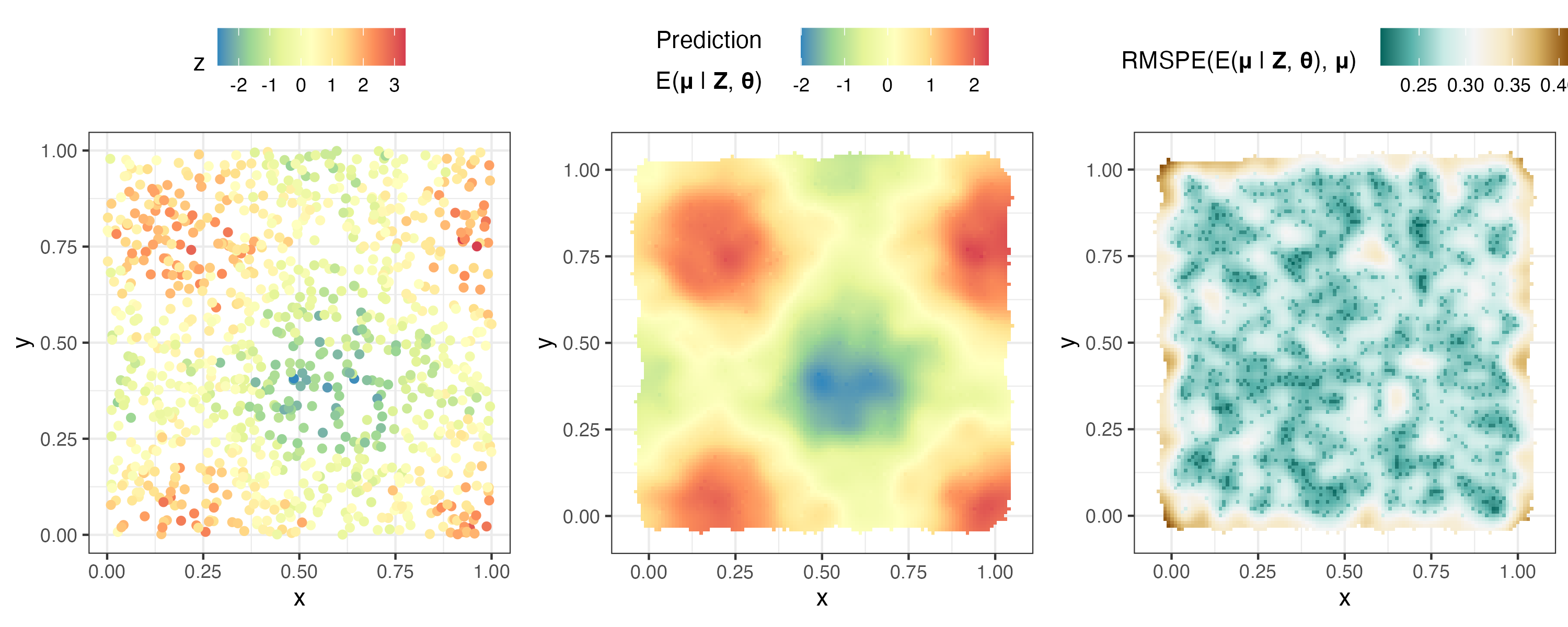
Ici, nous analysons les données de Poisson simulées. Nous signifions un modèle de données de Poisson avec une réponse moyenne qui est modélisée à l'aide de la fonction de lien racine carrée en définissant response = "poisson" et link = "sqrt" dans FRK() . Les autres distributions de réponse non gaussiennes disponibles dans FRK sont les distributions binomiale, binomiale négative, gamma et gaussienne inverse.
# # Simulate Poisson data using the previous example's data to construct a mean
zdf $ z <- rpois( m , lambda = zdf $ z ^ 2 )
# # Run FRK
S <- FRK( f = z ~ 1 , list ( zdf ),
response = " poisson " , # Poisson data model
link = " sqrt " ) # square-root link function
pred <- predict( S )
# # Plotting
plotlist <- plot( S , pred $ newdata )
ggarrange( plotlist $ z , plotlist $ p_mu , plotlist $ interval90_mu ,
nrow = 1 , legend = " top " )
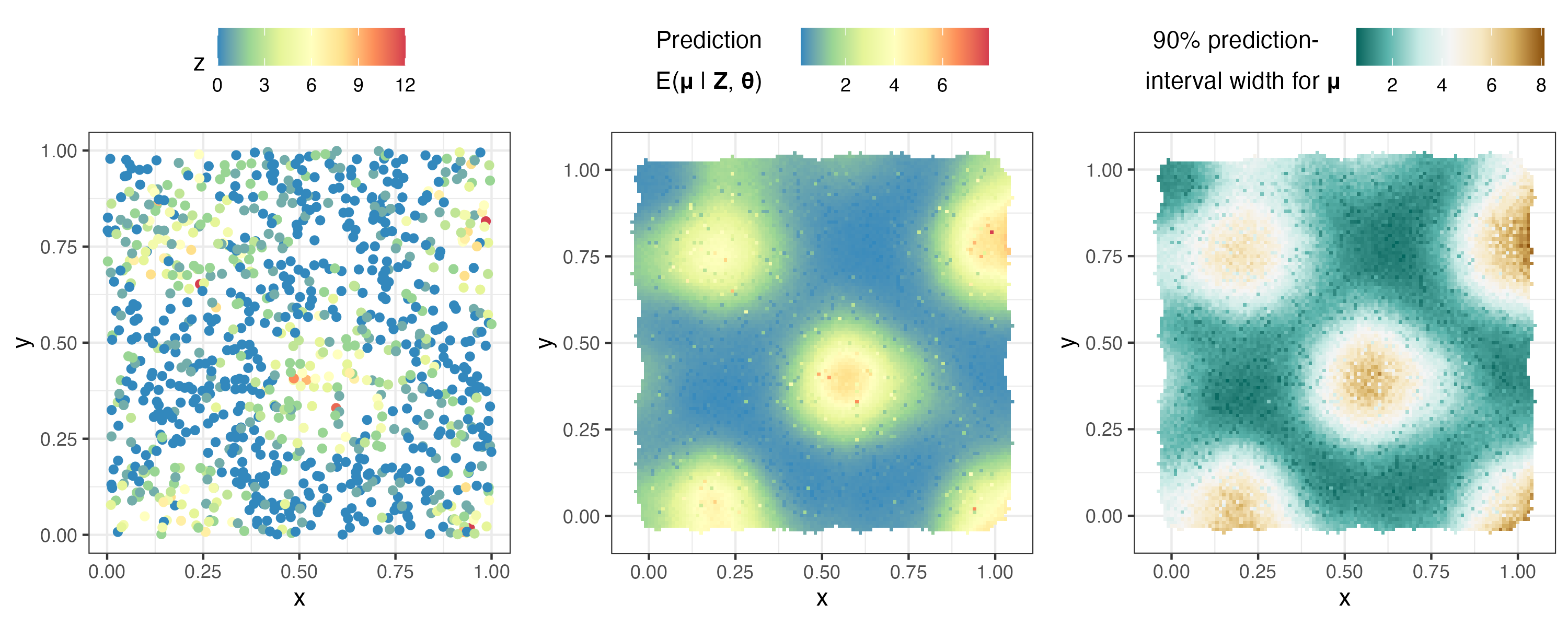
Nous analysons maintenant les données spatio-temporelles, en utilisant l'ensemble de données NOAA.
# # Setup
library( " spacetime " )
data( " NOAA_df_1990 " )
Tmax <- subset( NOAA_df_1990 , month %in% 7 & year == 1993 )
Tmax <- within( Tmax , { time = as.Date(paste( year , month , day , sep = " - " ))})
STObj <- stConstruct( x = Tmax , space = c( " lon " , " lat " ), time = " time " , interval = TRUE )
# # BAUs: spatial BAUs are 1x1 pixels, temporal BAUs are 1 day intervals
BAUs <- auto_BAUs( manifold = STplane(),
cellsize = c( 1 , 1 , 1 ),
data = STObj , tunit = " days " )
BAUs $ fs <- 1 # scalar fine-scale variance matrix, implicit in previous examples
# # Basis functions
G <- auto_basis( manifold = STplane(), data = STObj , nres = 2 , tunit = " days " )
# # Run FRK
STObj $ std <- 2 # fix the measurement error variance
S <- FRK( f = z ~ 1 + lat , data = list ( STObj ),
basis = G , BAUs = BAUs , est_error = FALSE , method = " TMB " )
pred <- predict( S , percentiles = NULL )
# # Plotting: include only some times via the argument subset_time
plotlist <- plot( S , pred $ newdata , subset_time = c( 1 , 7 , 13 , 19 , 25 , 31 ))
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )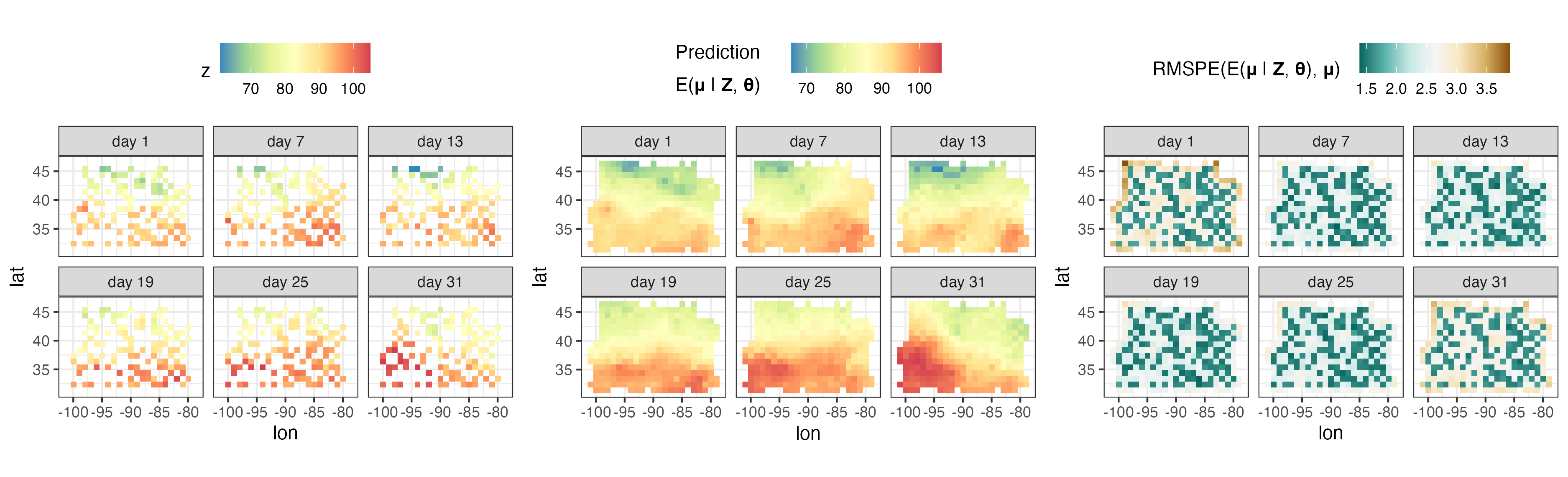
Le package FRK est actuellement utilisé pour générer des animations spatio-temporelles de champs observés par des données satellitaires. Nous montrons ici une prévision quotidienne du CO2 à l'aide des données de la NASA OCO-2 entre septembre 2014 et juin 2016.
Merci à Michael Bertolacci pour la conception du logo hexadécimal FRK !