Ces dernières années, les grands modèles de langage (LLM) ont montré des capacités étonnantes dans divers domaines, mais leurs capacités de raisonnement mathématique sont étonnamment faibles. L'éditeur de Downcodes interprétera pour vous une dernière étude, qui révèle l'incroyable "secret" du LLM en opérations arithmétiques, et analyse les limites de cette méthode et les orientations d'amélioration future. Cette recherche approfondit non seulement notre compréhension du mécanisme de fonctionnement interne du LLM, mais fournit également une référence précieuse pour améliorer les capacités mathématiques du LLM.
Récemment, les grands modèles de langage d'IA (LLM) ont bien performé dans diverses tâches, notamment l'écriture de poésie, l'écriture de code et le chat. Mais, pouvez-vous le croire ? se renversent souvent lors de la résolution de problèmes arithmétiques simples, ce qui est surprenant.
Une dernière étude a révélé le secret « étrange » derrière les capacités de raisonnement arithmétique de LLM : ils ne s'appuient ni sur des algorithmes puissants ni sur la mémoire, mais adoptent une stratégie appelée « méli-mélo heuristique » ! mais s'appuie sur un peu d'intelligence et de « règles empiriques » pour obtenir la réponse.
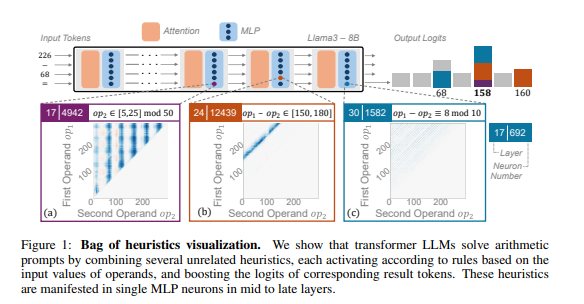
Les chercheurs ont utilisé le raisonnement arithmétique comme tâche typique et ont mené une analyse approfondie de plusieurs LLM tels que Llama3, Pythia et GPT-J. Ils ont découvert que la partie du modèle LLM responsable des calculs arithmétiques (appelée « circuit ») est composée de nombreux neurones individuels, dont chacun agit comme une « calculatrice miniature » et est uniquement responsable de la reconnaissance de modèles numériques spécifiques et de la sortie des données correspondantes. répondre. Par exemple, un neurone pourrait être chargé d'identifier les « nombres dont le chiffre unique est 8 », tandis qu'un autre neurone pourrait être chargé d'identifier « les opérations de soustraction dont les résultats sont compris entre 150 et 180 ».
Ces « mini-calculatrices » sont comme un fouillis d'outils, et au lieu de les utiliser selon un algorithme spécifique, LLM utilise une combinaison aléatoire de ces « outils » pour calculer une réponse basée sur le modèle de nombres qu'il saisit. C'est comme un chef qui n'a pas de recette fixe, mais qui la mélange à volonté en fonction des ingrédients disponibles, et qui finit par faire une « cuisine noire ».
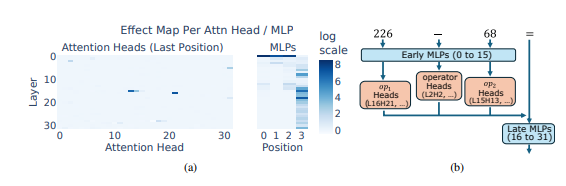
Ce qui est encore plus surprenant, c'est que cette stratégie de « mélange heuristique » est effectivement apparue dès les premiers stades de la formation LLM et a été progressivement améliorée au fur et à mesure de la progression de la formation. Cela signifie que le LLM s’appuie dès le départ sur cette approche de raisonnement « patchwork », plutôt que de développer cette stratégie à un stade ultérieur.
Alors, quels problèmes cette méthode de raisonnement arithmétique « étrange » va-t-elle causer ? Les chercheurs ont découvert que la stratégie du « méli-mélo heuristique » a une capacité de généralisation limitée et est sujette aux erreurs. En effet, LLM a un nombre limité de « petites intelligences », et ces « petites intelligences » elles-mêmes peuvent également avoir des défauts qui les empêchent de donner des réponses correctes lorsqu'elles rencontrent de nouveaux modèles numériques. Tout comme un chef qui ne sait faire que des "œufs brouillés à la tomate", si on lui demande soudain de faire du "porc effiloché au goût de poisson", il sera certainement pressé et désemparé.
Cette étude a révélé les limites de la capacité de raisonnement arithmétique du LLM et a également indiqué la direction à suivre pour améliorer la capacité mathématique du LLM à l'avenir. Les chercheurs estiment que s'appuyer uniquement sur les méthodes de formation et l'architecture de modèle existantes pourrait ne pas suffire à améliorer les capacités de raisonnement arithmétique de LLM, et que de nouvelles méthodes doivent être explorées pour aider LLM à apprendre des algorithmes plus puissants et plus généraux afin qu'ils puissent véritablement devenir des « maîtres mathématiques ».
Adresse papier : https://arxiv.org/pdf/2410.21272
Dans l’ensemble, cette étude fournit une analyse approfondie des stratégies « étranges » du LLM en matière de raisonnement mathématique, nous offre une nouvelle perspective pour comprendre les limites du LLM et indique la direction des recherches futures. Je crois qu'avec le développement continu de la technologie, les capacités mathématiques de LLM seront considérablement améliorées.