
と React の Fiber タスクについて理解しておく必要があります。また、Fibre タスクごとに、優先度の高いタスクを最初に処理する必要があります。たとえば、ユーザーのクリックと入力は、ユーザー エクスペリエンスを向上させるために、ユーザーの操作が即座に効果をもたらすことが確実に求められるため、優先度の高いタスクです。たとえば、アニメーション イベントの優先順位は低くする必要があります。新しい優先度の高いタスクがキューに入ったら、React は最初にそれを処理する必要があります。
これらのタスクを保存するために、React には 2 つのタスク プールがあります。
// タスクは最小ヒープに保存されます var taskQueue = []; var timerQueue = [];
taskQueue と timerQueue は両方とも配列であり、前者はすぐに実行されるタスクを格納し、後者は遅延する可能性のあるタスクを格納します。
var newTask = {
id: taskIdCounter++, // タスク ID をマークします
callback, // コールバック関数 priorityLevel, // タスクの優先度 startTime, // タスクの開始時刻、時点 ExpirationTime, // 有効期限、時点 sortIndex: -1, // タスクの並べ替え、値は有効期限から取得されるため、値が小さいほど優先度が高くなります。 React に新しいタスクが来ると、まず currentTime を使用して現在の時刻を記録します (タスクに遅延パラメータを指定すると、タスクの実行時間が開始されます。次に、startTime > currentTime が成立する場合、タスクを延期できることが証明され、タスクは timerQueue に入り、そうでない場合は taskQueue に入ります。
React はどのようにして最も優先度の高いタスクを見つけますか? taskQueue を例に挙げます。これは動的タスク プール (タスク キュー) であり、データ形式は配列です。もちろん、優先度に従って並べ替えることもできます (Array.sort)。新しいタスクがキューに追加されると、最初に並べ替えられ、次に優先度が最も高いタスクが検索されて実行されます。ただし、Array.sort の平均時間計算量は O(nlogn) であり、これは最良の解決策ではありません。
SortIndex は、taskQueue の newTask でのソートに使用されます。この値は有効期限から取得されます。つまり、優先度が高いタスクほど、理解して実行する必要があるため、有効期限は短くなります。優先度が高くなるほど、有効期限が短くなり、当然、sortIndex も小さくなります。実際、これは優先キューです。
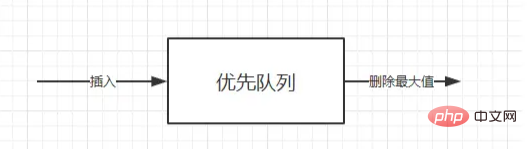
優先キューもキューの一種です (第一に、これはキューであり、第二に、後入れ先出しです)。唯一の違いは、優先キューのデキュー順序が優先順位に基づいていることです。要素セット内の最小要素または最大要素は、優先キュー ADT を使用して操作できます。優先キュー ADT は、最小値の操作 (最小要素の返しと削除) の挿入と削除をサポートするデータ構造です。最大値の削除操作 (最小要素を返して削除)、最大要素を削除します。
最小のキー値を持つ要素の優先順位が最も高い場合、この優先キューは昇順優先キューと呼ばれます (つまり、最小の要素が常に最初に削除されます)。同様に、最大のキー値を持つ要素の優先順位が最も高い場合、このタイプの優先キューは降順優先キューと呼ばれます (つまり、最大の要素が常に最初に削除されます)。これら 2 つのタイプは対称であるため、必要なのは次のとおりです。優先順位の高いキューなど、そのうちの 1 つに焦点を当てます。
たとえば、私たちがチケットを買うとき、私たちは全員列に並んでいて、列の前にいた人が最初にチケットを買うことになりました。しかしその後、兵士が来て、その人がより高い優先権を持って列に並びました。正面。
React では、この機能を実現するために最小ヒープ(小さなルート ヒープ、小さなトップ ヒープなど) が使用されます。つまり、taskQueue を最小ヒープに変換し、実行のために最上位のタスクを取り出し、taskQueue をヒープし、それを最小ヒープ データ構造として維持します。新しいタスクを taskQueue に挿入するときは、タスクをヒープ化し、常に最小のヒープとして保持する必要があります。
: ヒープは優先キューと呼ばれることもあります (正確ではありません)。まず、これはキューであり、「先入れ先出し」というキューの特性を持っています。 。次に、このキュー内の要素には優先順位があり、優先順位の高い要素が最初にランク付けされます。
正確に言うと、ヒープは優先キューを実装する方法です。もちろん、優先キューは他の方法でも実装できます。
ヒープ ソートは不安定なソートであると前に述べましたが、taskQueue はこのプロセスが安定していることを望んでいます。つまり、2 つのタスクの有効期限が同じである可能性がある場合、それは誰が入力するかによって決まります。まず、タスク プールは newTask の ID の値であり、新しいタスクが来るたびに ID が 1 ずつ増加します。
関数比較(a, b) {
// 最初にソートインデックスを比較し、次にタスク ID を比較します。
const diff = a.sortIndex - b.sortIndex;
diff を返します !== 0 ? diff : a.id - b.id;
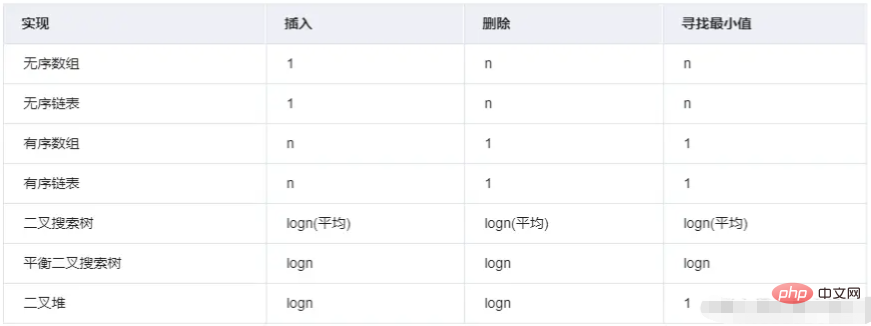
最小
ヒープを理解する前に、基礎知識を確認しましょう。
ツリー内のノードの次数が 2 以下である順序付きツリーを指します。これは、最も単純で最も重要なツリーです。
子ノードを持たない最後のレベルを除き、各レベルのすべてのノードが 2 つの子ノードを持つバイナリ ツリーです。
グラフィカルな観点から見ると、完全なバイナリ ツリーは三角形のように見えます。
バイナリ ツリーのレベル数が K で、ノードの総数が (2^k) -1 の場合、それは完全なバイナリ ツリーです。
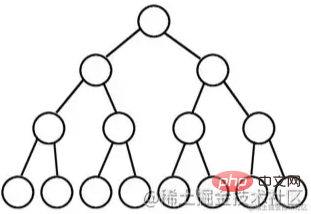
完全二分木とは「娘には両面がある」という意味で、非常に完全であるため、完全二分木と呼ばれます。
葉ノードを除いて、すべてのノードの次数は 2 です。つまり、すべてのノードの次数は 0 または 2 のみになります。
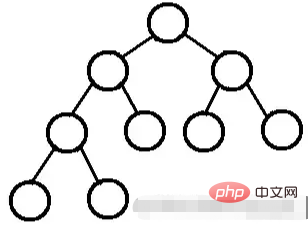
完全な二分木には子がないか、両方の子が存在します。
Full Binary Tree の英語原文:
完全バイナリ ツリー (FBT) は、葉以外のすべてのノードに 2 つの子があるツリーです。
完全バイナリ ツリーの英語の原文:
完全バイナリ ツリー (PBT) は、すべてのリーフ ノードが同じ深さにあるツリーです。すべての内部ノードは次数 2 を持っています。
すべての外国の本は完全二分木と完全二分木に関する最初の翻訳された教科書を参照していますが、最初に翻訳された記事は誤って翻訳されています。現在、中国では、間違いを犯すことができるのは、間違いが間違っている場合だけです(誰もが間違っているので、間違っている人も正しいことになります。たとえば、ロビイスト…)。外国人の友人とこれら 2 つの概念について話し合いたい場合は、注意する必要があります。
バイナリ ツリー (CBT) は、おそらく最後のレベルを除くすべてのレベルが完全に埋められ、すべてのノードが可能な限り左にある
、深さ k の n 個のノードを持つバイナリ ツリー
です。上から下、左から右に i (1≤i≤n) という番号のノードが 2 分木にあり、その位置が同じであれば、2 分木は次のようになります。完全二分木と呼ばれます。
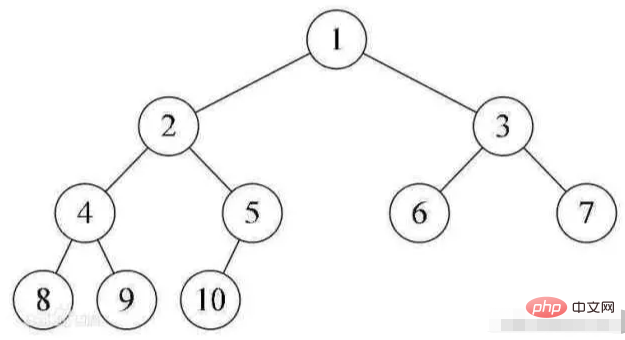
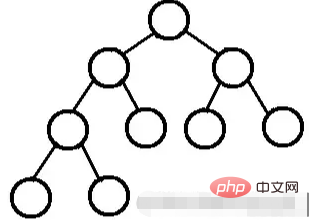
ヒープは常に次の特性を満たします。
まず、ビッグ ルート ヒープを理解する必要があります。小さなルート ヒープ 完全なバイナリ ツリーでは、すべてのノードがその子ノードよりも大きい (または小さい) ため、ここには最大ヒープと最小ヒープの 2 つの状況が存在します。
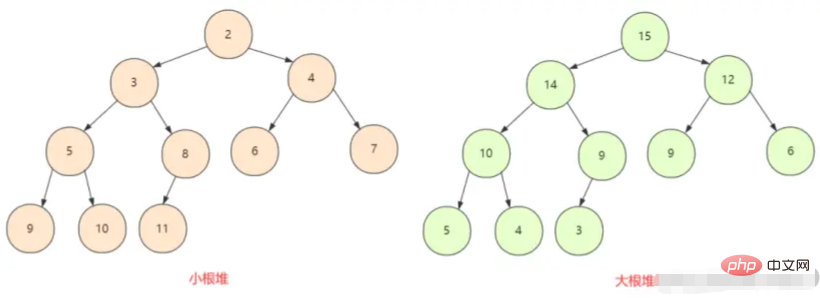
ヒープは通常、完全なバイナリ ツリーとして表示できるオブジェクトの配列です。もちろん、バイナリ ツリーは配列で表すこともできます。
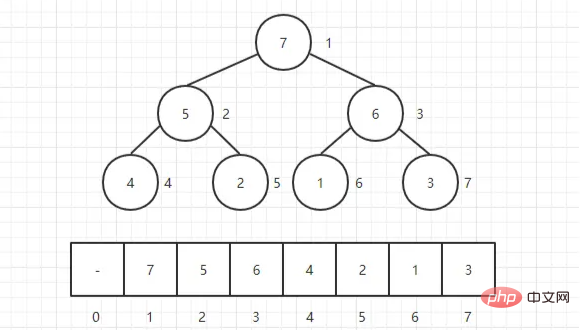
、最初にヒープを構築してからそれを調整することです。
バイナリ ツリー (配列表現) の、「最初の非リーフ ノード」から順に下から上に調整します。調整のルールは次のとおりです。
ヒープの構築は O(n) です。 ) 時間計算量のプロセス。
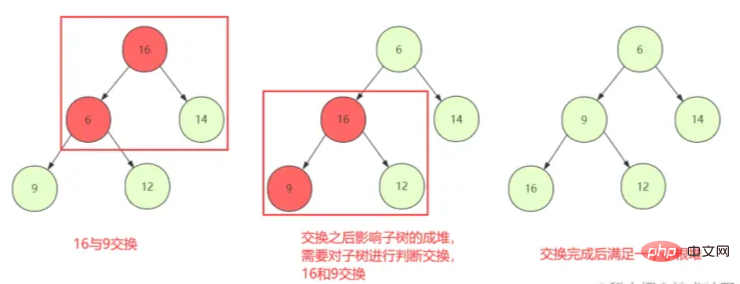
① 現在のノードと子ノードがヒープのプロパティを維持できるように、最初の非リーフ ノードからスワップ ダウン (shiftDown) を判断します。
② ただし、交換によってヒープ構造のプロパティが壊れる場合は、通常のノードの置き換えは問題にならない可能性があります。子のノードを削除した場合は、停止するまでスワップされたノードを再度 ShiftDown する必要があります。
ヒープ
構造を調整したヒープ構造が破壊される可能性があります。
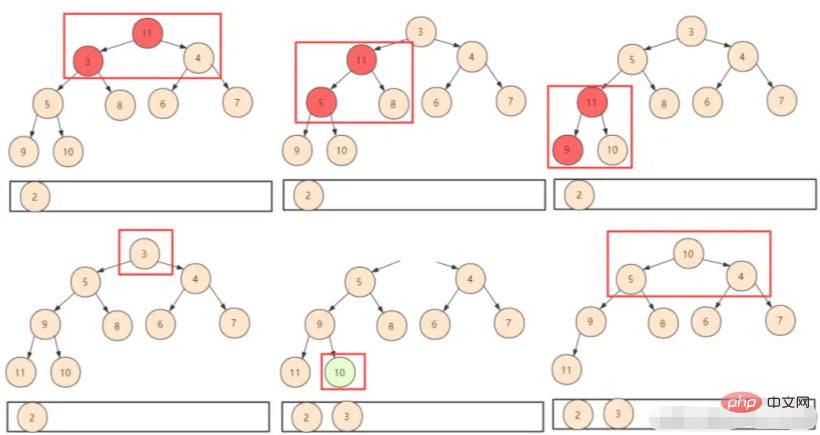
① したがって、単純に最後の要素を最初に置きます。このように、スワップシフト(shiftDown)を判定するだけで済みますが、このときヒープ全体のサイズが変化していることに注意する必要があります。論理的には破棄位置を使用しないため、ヒープを含める必要があります。関数を設計するときの size パラメーター。
② ヒープ内の要素がすべて取得されるまで上記の操作を繰り返します。
ヒープ アルゴリズムの複雑さの分析に関して、以前のヒープ構築時間の複雑さは O(n) でした。ヒープの上部が削除されてから下にスワップされるたびに、それぞれの番号が記録されます。このように、計算量は O(nlogn) となり、合計時間計算量は O(n)+O(nlogn)=O(nlogn) となります。
コレクションの最大値を維持するのに適しています。
要素がヒープからポップアウトされた後、ヒープの最上位要素 (つまり、2 番目に高い値) を取得するために再調整するコストは比較的低くなります。これは、要素がポップアウトされた後、ヒープは準領域になるためです。もちろん、コストは比較的低く、時間計算量は O(logn) ですが、2 番目に高い値を見つけるために 1 回走査すると、次のようになります。時間計算量は O(n) です。
コードは Javascript ES6 で記述されています。
クラス ヒープ {
コンストラクター(データ、コンプ) {
this.data = データ データ: [];
// 比較ルール: より柔軟に値またはオブジェクトを比較できます this.compartor = comp ? comp : (ab) => ab;
// ヒープ(優先キュー)に合わせて調整
this.heapify();
}
heapify() {
if(this.size() <= 1) 戻り値;
// 最初の非リーフ ノードから調整を開始するか、最後の要素から調整することもできます for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//ヒープを調整します。下方調整は再帰を使用して実装することもできます。ここでは、反復を使用して this.shiftDown(i) を実装します。
}
}
// 下方向に調整しますshiftDown(i) {
左 = 2*i +1 とします。
右 = 2*i +2 とします。
let len = this.size();
while(i < len) {
findIndex = i にします。
//左の子の方が「大きい」
if(left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
findIndex = 左;
}
// 右側の子の方が「大きい」
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = 右;
}
if(i !== findIndex) {
// 現在のノードをより大きな値と交換 [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// この層を調整した後、下位層のヒープの特性に影響を与える可能性があるため、下位層の調整を続けます (反復実装または再帰的)
i = インデックスを見つける;
左 = 2*i +1;
右 = 2*i +2;
}
それ以外 {
// 調整が必要ない場合は、飛び出します (飛び出しなければループは終了しません)
壊す;
}
}
}
// 上方向に調整しますshiftUp(i){
// 親の添字を検索します letparentIndex = Math.floor((i-1)/2);
// 最大値を 0 に調整します
while(parentIndex >=0 ) {
findIndex = i にします。
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = 親インデックス;
}
if(findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = インデックスを見つける;
parentIndex = Math.floor((i-1)/2);
}
それ以外 {
壊す;
}
}
}
// ヒープ内のすべての要素の数を取得します size(){
this.data.length を返します。
}
// ヒープの最初の要素を取得します Peak(){
if(!this.size()) は null を返します。
this.data[0] を返します;
}
// 要素をヒープに追加します Push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// ヒープから最初の要素をポップします Pop(){
if(!this.size()) は null を返します。
let res = this.data[0];
if(this.size() == 1) {
this.data.pop();
}
それ以外 {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
this.shiftDown(0);
}
応答を返します。
}
let arr = [2,9,8,6,3,10,5,7,4,1];
。
comp = (a, b) => ab; とします。
let heap = new Heap(arr, comp);
res = []; とします。
while(heap.size()) {
res.push(heap.pop());
}
console.log(res); arr の要素はオブジェクトにすることもできます。
React ソース コード内のディレクトリ package/scheduler は、React のタスク スケジューリング モジュールに関連するコードです。
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* 著作権 (c) Facebook, Inc. およびその関連会社。
*
* このソース コードは、次の MIT ライセンスに基づいてライセンスされています。
* このソース ツリーのルート ディレクトリにある LICENSE ファイル。
*
* @flow strict
*/
タイプ ヒープ = Array<ノード>;
タイプ ノード = {|
ID:番号、
sortIndex: 数値、
|};
エクスポート関数プッシュ(ヒープ: ヒープ、ノード: ノード): void {
const インデックス = ヒープの長さ;
ヒープ.プッシュ(ノード);
siftUp(ヒープ、ノード、インデックス);
}
エクスポート関数 Peak(ヒープ: ヒープ): ノード |
const first = ヒープ[0];
最初に返す === 未定義 null : 最初に;
}
エクスポート関数 Pop(ヒープ: ヒープ): ノード |
const first = ヒープ[0];
if (最初の !== 未定義) {
const last = heap.pop();
if (最後 !== 最初) {
ヒープ[0] = 最後;
siftDown(ヒープ、最後、0);
}
最初に戻ります。
} それ以外 {
null を返します。
}
}
関数 siftUp(ヒープ, ノード, i) {
インデックス = i とします。
while (true) {
constparentIndex = (インデックス - 1) >>> 1;
const 親 = ヒープ[親インデックス];
if (親 !== 未定義 && 比較(親, ノード) > 0) {
// 親の方が位置を交換します。
ヒープ[親インデックス] = ノード;
ヒープ[インデックス] = 親;
インデックス = 親インデックス;
} それ以外 {
// 親のほうが小さいです。
戻る;
}
}
}
関数 siftDown(ヒープ, ノード, i) {
インデックス = i とします。
const 長さ = ヒープの長さ;
while (インデックス < 長さ) {
const leftIndex = (インデックス + 1) * 2 - 1;
const left = ヒープ[leftIndex];
const rightIndex = leftIndex + 1;
const right = ヒープ[rightIndex];
// 左または右のノードが小さい場合は、小さい方のノードと交換します。
if (left !== 未定義 && Compare(left, ノード) < 0) {
if (right !== 未定義 && Compare(right, left) < 0) {
ヒープ[インデックス] = 右;
ヒープ[rightIndex] = ノード;
インデックス = rightIndex;
} それ以外 {
ヒープ[インデックス] = 左;
ヒープ[leftIndex] = ノード;
インデックス = 左インデックス;
}
else if (right !== 未定義 && Compare(right, node) < 0) {
ヒープ[インデックス] = 右;
ヒープ[rightIndex] = ノード;
インデックス = rightIndex;
} それ以外 {
// どちらの子も小さくありません。
戻る;
}
}
}
関数比較(a, b) {
// 最初にソートインデックスを比較し、次にタスク ID を比較します。
const diff = a.sortIndex - b.sortIndex;
diff を返します !== 0 ? diff : a.id - b.id;
私たちが実装した最小ヒープは
React の実装とは若干異なりますが、考え方は同じで、コードの書き方が異なるだけです。
React のタスク スケジューリングは最小ヒープを使用して実装されます。最小ヒープについてある程度理解していれば、この内容をより早く学ぶことができます。個人的には、初期段階での知識の蓄積がいかに重要であるかは考えていますが、そのプロセスは退屈かもしれません。 この時点で、いくつかのアルゴリズムを知っていると思いますか? 実際、これらのアルゴリズムは入門レベルであり、まだ始めてもいません。なぜなら、React のタスク スケジューリング シナリオでは、実装する要件が非常に明確であり、使用するデータ構造とアルゴリズムも明確だからです。実際のシナリオでは、特定の要件はわかっていますが、どのようなデータ結果とアルゴリズムを使用するかはわかりません。要件を抽象化し、抽象データ モデルに基づいて具体的なデータ構造とアルゴリズムを設計する必要があります。 。