정규 분포를 사용한 MLE - 연구실

소개

이 실습에서는 MLE가 정규 분포와 어떻게 작동하는지 알아보기 위해 이전 강의에서 본 수학 공식을 실제로 적용해 보겠습니다.

목표

당신은 다음을 할 수 있습니다:

MLE가 정규 분포와 어떻게 작동하는지 이해하고 설명합니다.
평균과 분산을 식별하여 주어진 데이터에 정규 분포를 맞춥니다.
적합 분포와 실제 분포를 시각적으로 비교

참고: *증명을 포함한 모든 MLE 방정식의 자세한 파생 내용은 이 웹사이트에서 볼 수 있습니다. *

Python의 MLE

아래에서 Python을 사용한 MLE 및 분포 피팅의 예를 살펴보겠습니다. 여기서 scipy.stats.norm.fit 최대 가능성 추정을 사용하여 분포 매개변수를 계산합니다.

필요한 라이브러리 가져오기

 from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np

평균이 0이고 stdv가 1인 정규 거리에서 200개의 무작위 샘플 배열을 생성합니다.

 sample = None

MLE를 통한 분포 피팅

- 위 데이터에 분포를 맞추려면 `stats.norm.fit(data)` 를 사용하세요.

- 이는 MLE 접근 방식을 통해 (평균,: 매개변수[0] 및 표준: 매개변수[1])의 두 매개변수 목록을 반환합니다.

 param = None

#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)

a) 실제 데이터 매개변수 b) `x = np.linspace(-5,5,100)` 를 사용하여 피팅된 매개변수로부터 PDF를 계산합니다.

 x = np . linspace ( - 5 , 5 , 100 )

# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None

두 PDF 모두 시각화

 # Your code here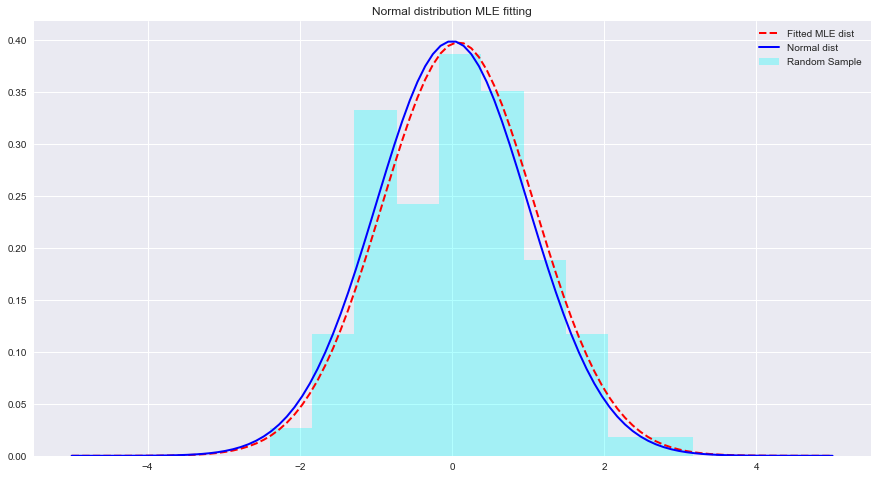

png

 #  Your comments/observations

요약

이 짧은 실습에서는 가우스 맥락, 즉 기본 무작위 변수가 정규 분포를 따르는 베이지안 설정을 살펴보았습니다. 우리는 MLE가 예상 평균의 가능성을 최대화하여 정규 분포의 알려지지 않은 매개변수를 추정할 수 있다는 것을 배웠습니다. 예상 평균은 해당 매개변수 공간 내에서 적합하지 않은 정규 분포의 평균에 매우 가깝습니다. 우리는 Naive Bayes Classifier를 사용하여 데이터 분포에 존재하는 여러 클래스의 수단을 추정할 때 이러한 추정이 어떻게 수행되는지 학습하는 방향으로 이러한 이해를 진행할 것입니다.

확장하다

추가 정보