FiberFold

데스크톱 프린터에서 3D 인쇄를 수행하는 웹앱입니다.

이 프로젝트는 이전 eMesh 데스크탑 애플리케이션(SDL, openGL2, C++)을 (js) 다시 작성한 것입니다.

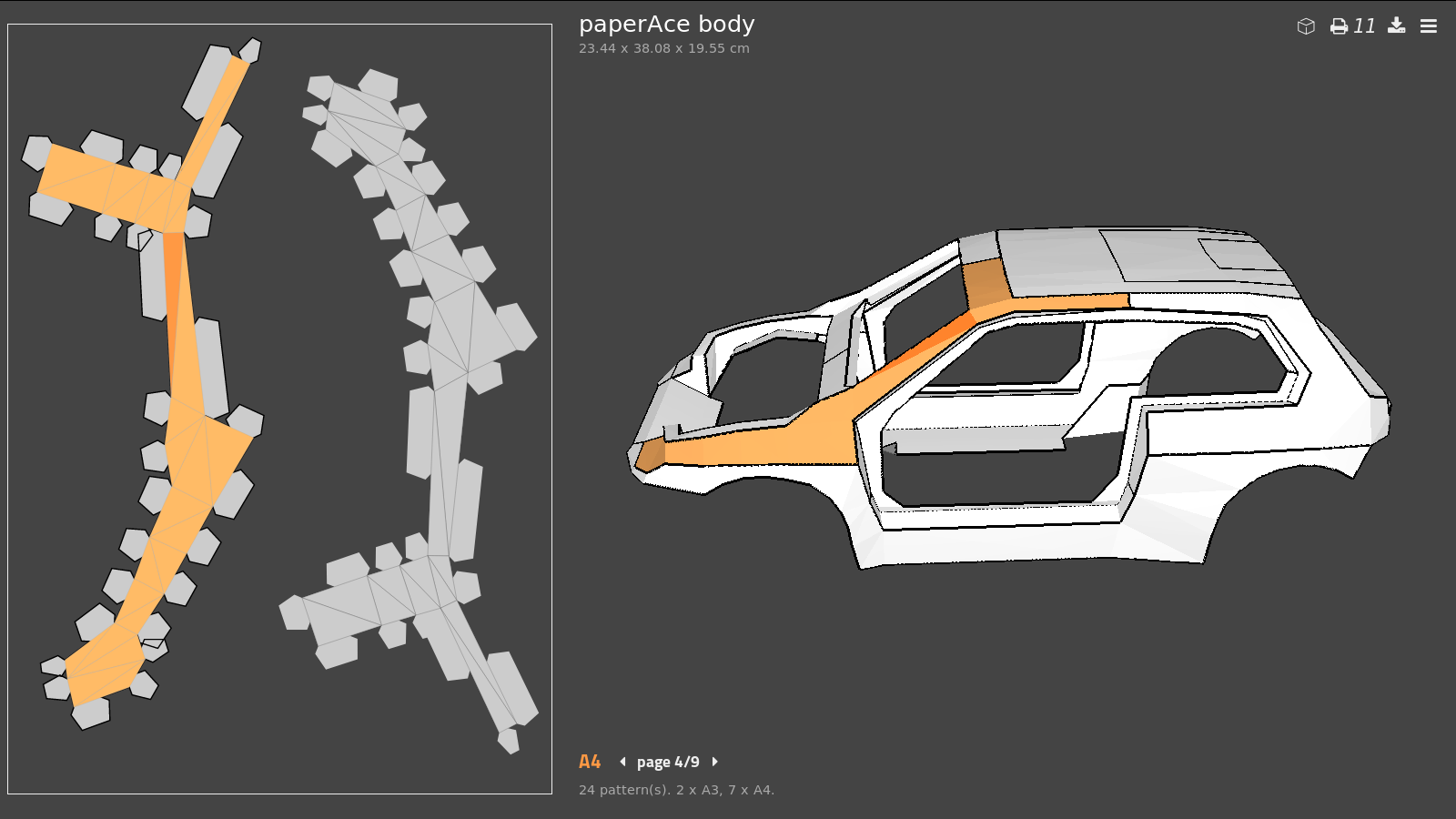
대체 프로토타이핑 도구(paperAce와 마찬가지로)로 사용할 수 있는 충분한 고급 종이 제작 도구를 제공하는 것이 목표입니다. 사용이 가능한 한 간단하다는 것 외에.

여기에 기능적인 것의 시작이 있습니다. 그것을 시도하십시오!

터치 장치는 아직 완전히 지원되지 않으며 곧 지원될 예정입니다.

상태

FreakPOC - [합리적으로 안전한 개념 증명] - 출시 후보

목표 :

• 대체 프로토타이핑 도구로 사용할 수 있는 충분한 고급 종이 제작 도구를 제공합니다(paperAce가 제공하는 것처럼).
• 최대한 간단하게 사용하세요.

비목표:

• 텍스처링.
• 메쉬 편집.

요구사항

webGL을 제공하는 브라우저입니다.

진행 방법

모든 작업을 수행하는 방법은 단 하나뿐입니다.

• 패턴을 만듭니다.
• 패턴을 확장합니다.
• 패턴을 병합합니다.
• 패턴 분할.

두 개의 연결된 삼각형을 연속적으로 누르십시오.

두 개의 결합된 삼각형을 연속적으로 쳤을 때 두 삼각형이 공유하는 가장자리를 동결이라고 합니다. 이미 고정된 경우 고정이 해제됩니다.

내부 작업:

• 전역(사용자 단계)

  동결된 모서리는 패턴의 주요 구성요소입니다. 조립하려는 삼각형을 연결하여 하나를 만듭니다. Papier가 수행하는 작업에서 먼저 각 삼각형의 좌표를 계산하여 동일한 평면에서 이동합니다. 그런 다음 그는 패턴을 조립하고 삼각형으로 연결된 고정된 가장자리를 찾습니다. 패턴에 속하지만 고정되지 않은 삼각형에 인접해 있는 모서리는 이제 패턴 테두리로 간주될 수 있습니다. 이제 이러한 데이터를 통해 정렬된 노드 체인 형태로 평평한 패턴의 경계를 나타내는 것이 가능합니다.

• 단계별 내부 작업 :

  가장자리 고정 시도 후 처리가 수행되기 전에 모든 패턴의 재구성, 패턴 사본이 완료됩니다. 정지 시도가 실패하면 앱 상태를 복원합니다.

  • 삼각형 편평화

    삼각형을 평평하게 만듭니다. 파피어의 존재 이유! 이 단일 단계는 데스크탑 프린터에서 3D 프린팅을 수행하는 데 충분할 수 있습니다. 이 단계는 코드 측면에서도 상황을 약간 복잡하게 만듭니다. 대부분의 메시와 마찬가지로 "파면"은 먼저 3D 모델의 꼭지점을 설명한 다음 이 꼭지점을 사용하여 삼각형을 설명합니다. 그러나 제대로 평탄화하려면 이제 삼각형이 자체 정점 좌표를 저장해야 합니다. 이는 메쉬 정상이 여러 개의 편평한 삼각형 정상으로 표현될 수 있다는 의미입니다. 그런 다음 이러한 정점은 해당 정점에 해당하는 메시 정점의 식별자(실제로는 인덱스)를 저장합니다.

  • 패턴 조립

표준 및 기술:

• 자바스크립트
• WebGL( three.js를 통해 )
• SVG
• HTML
• CSS

타사 코드 라이브러리:

• Three.js
• Hammer.js(터치 장치 호환성을 제공하기 위해 곧 출시 예정)
• jQuery

할 일 :

• 패턴 최종 레이아웃을 자동화합니다.
• 완전한 모바일 장치 지원.
• 코드 디자인을 깔끔하고, 아름답게 하고, 명확하게 만듭니다.
• 계속하려면 자금을 확보하세요.
• 오토클레이브 탭을 생성할 수 있도록 합니다.
• 조립 표시를 생성할 수 있도록 합니다.
• 레이저 절단 호환 문서를 생성할 수 있습니다.
• 패턴 선택을 자동화합니다.
• 구성 옵션을 풍부하게 합니다.
• OOP 재작성.

완료:

• 애플리케이션 레이아웃.
• 3D 사용자 모델을 로드합니다.
• 수동 패턴 편집.
• 대체 패턴 편집 모드(빠른 방법)를 추가했습니다.
• 패턴 평탄화.
• 확장 기능.

저자

• 토마스 세인트 피에르 - 초기 작업 | 코드 엔지니어링 s1pierro

특허

코드는 GNU GPL v3의 조건에 따라 라이센스가 부여됩니다.

그러한 종류의 앱에 관심이 있고 더 많은 앱을 원하거나 기여하고 싶다면 언제든지 저에게 연락하세요: [email protected]

피드백

자유롭게 이슈를 열어보세요.