Os modelos de linguagem grande (LLM) mostram habilidades incríveis em muitos campos.研究人员深入分析了 llama3 、 pythia 和 gpt-j 等多个 llm , 发现它们并非依靠强大的算法或记忆力进行计算 , 而是采用一种 而是采用一种 启发式大杂烩 启发式大杂烩 的策略 , 如同一个靠 如同一个靠 小聪明 小聪明 和 和 ““ A lei das respostas empíricas "mongóis.
Recentemente, o Modelo de Linguagem de AI (LLM) teve um bom desempenho em várias tarefas. Eles geralmente se entregam ao lidar com perguntas aritméticas simples, o que é surpreendente.
Um estudo mais recente revela o segredo "maravilhoso" por trás das capacidades de raciocínio aritmético LLM: eles não dependem de algoritmos fortes nem dependendo da memória, mas usam uma estratégia chamada "Inspiração de Hodgepody"! Teoremas com cuidado, mas confiam em algumas "pequenas inteligência" e "regras da lei" para responder.
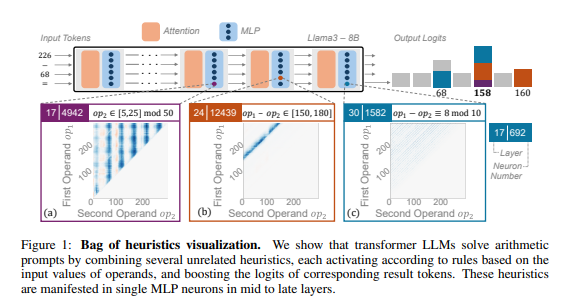
Os pesquisadores usam o raciocínio aritmético como tarefas típicas para realizar análises aprofundadas de vários LLMs, como LLAMA3, Pythia e GPT-J. Eles descobriram que o modelo LLM é responsável pelo cálculo aritmético (chamado "circuito") que consiste em muitos neurônios únicos. Modo digital e saída a resposta correspondente da correspondência. Por exemplo, um neurônios pode ser responsável por identificar "números com 8 dígitos", e outro neurônio é responsável por identificar "operações de subtração entre 150 e 180".
Essas "calculadoras em miniatura" são como uma pilha de ferramentas confusas. É como um chef, não há receita fixa, mas nos ingredientes existentes à mão e finalmente faz uma "cozinha escura".
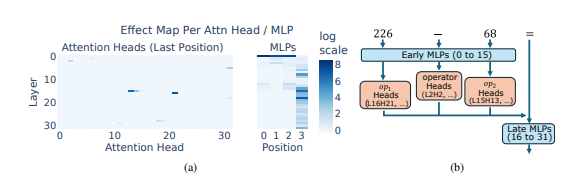
O que é ainda mais surpreendente é que essa estratégia "inspiradora hodgepodge" apareceu no início do treinamento da LLM e gradualmente melhorou com o treinamento. Isso significa que a LLM depende dessa "peças de peças" desde o início, em vez de desenvolver essa estratégia no período posterior.
Então, quais são os problemas desse método de raciocínio aritmético "maravilhoso"? Isso ocorre porque o número de "pequena inteligência" mantida pelo LLM é limitada, e esses "pouca inteligência" também podem ter defeitos em si mesmos, fazendo com que eles não possam dar a resposta correta quando encontrar um novo modelo digital. Assim como um chef que só fazia "ovos mexidos de tomate", ele de repente o fez fazer um "triturador ralado com sabor de peixe".
Este estudo revelou as limitações das capacidades de raciocínio aritmético da LLM e também apontou a direção para a melhoria futura das capacidades matemáticas da LLM. Os pesquisadores acreditam que confiar nos métodos de treinamento existentes e em arquiteturas de modelos podem não ser suficientes para melhorar as capacidades de raciocínio aritmético da LLM.
Endereço da tese: https://arxiv.org/pdf/2410.21272
Esta pesquisa não apenas explica a falta de LLM no cálculo da matemática, mas também fornece direções de referência valiosas para a melhoria futura do LLM. Em pesquisas futuras, precisamos prestar atenção em como melhorar a capacidade de generalização e algoritmo de aprendizado do LLM de resolver seus defeitos no raciocínio aritmético e torná -lo verdadeiramente poderosa capacidades matemáticas.