В последние годы модели больших языков (LLM) продемонстрировали удивительные возможности в различных областях, но их возможности математического рассуждения на удивление слабы. Редактор Downcodes интерпретирует для вас последнее исследование, которое раскрывает невероятный «секрет» LLM в арифметических операциях, а также анализирует ограничения этого метода и направления дальнейшего совершенствования. Это исследование не только углубляет наше понимание внутреннего механизма работы LLM, но также предоставляет ценную информацию для улучшения математических возможностей LLM.
В последнее время модели большого языка ИИ (LLM) хорошо зарекомендовали себя в различных задачах, включая написание стихов, написание кода и общение в чате. Они просто всемогущи! Но можете ли вы в это поверить? часто опрокидываются при решении простых арифметических задач, что удивительно.
Последнее исследование раскрыло «странный» секрет способностей LLM к арифметическому рассуждению: они не полагаются ни на мощные алгоритмы, ни на память, а используют стратегию, называемую «эвристической мешаниной»! но полагается на некоторую «небольшую сообразительность» и «практические правила», чтобы получить ответ.
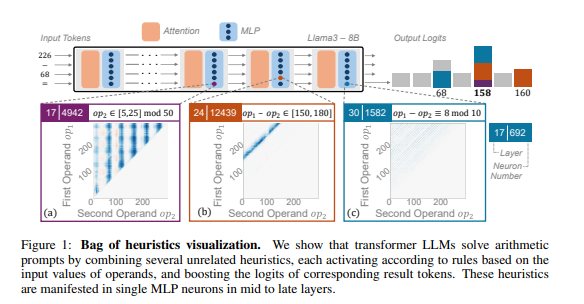
Исследователи использовали арифметические рассуждения в качестве типичной задачи и провели углубленный анализ нескольких LLM, таких как Llama3, Pythia и GPT-J. Они обнаружили, что часть модели LLM, отвечающая за арифметические вычисления (называемая «схемой»), состоит из множества отдельных нейронов, каждый из которых действует как «миниатюрный калькулятор» и отвечает только за распознавание конкретных числовых шаблонов и выдачу соответствующих результатов. отвечать. Например, один нейрон может отвечать за идентификацию «числ, у которых одна цифра равна 8», а другой нейрон может отвечать за идентификацию «операций вычитания, результаты которых находятся между 150 и 180».
Эти «мини-калькуляторы» подобны набору инструментов, и вместо того, чтобы использовать их в соответствии с определенным алгоритмом, LLM использует случайную комбинацию этих «инструментов» для расчета ответа на основе набора введенных чисел. Это похоже на шеф-повара, у которого нет фиксированного рецепта, но он смешивает его по своему желанию на основе имеющихся под рукой ингредиентов и, наконец, готовит «темную кухню».
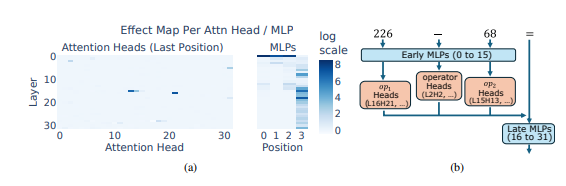
Что еще более удивительно, так это то, что эта стратегия «эвристической мешанины» на самом деле появилась на ранних этапах обучения LLM и постепенно улучшалась по мере прохождения обучения. Это означает, что LLM с самого начала полагается на этот «лоскутный» подход к рассуждениям, а не разрабатывает эту стратегию на более позднем этапе.
Итак, какие проблемы вызовет этот «странный» арифметический метод рассуждения? Исследователи обнаружили, что стратегия «эвристическая мешанина» имеет ограниченную способность к обобщению и склонна к ошибкам? Это связано с тем, что LLM имеет ограниченное количество «маленьких хитростей», и эти «маленькие хитрости» сами по себе также могут иметь недостатки, которые не позволяют им давать правильные ответы при обнаружении новых числовых моделей. Точно так же, как повар, который умеет готовить только «томатную яичницу», если его вдруг попросят приготовить «шинкованную свинину с рыбным вкусом», он обязательно поторопится и растеряется.
Это исследование выявило ограничения способностей LLM к арифметическому рассуждению, а также указало направление улучшения математических способностей LLM в будущем. Исследователи полагают, что полагаться исключительно на существующие методы обучения и архитектуру модели может быть недостаточно для улучшения возможностей LLM по арифметическому рассуждению, и необходимо изучить новые методы, которые помогут LLM освоить более мощные и общие алгоритмы, чтобы они действительно могли стать «мастерами математики».
Адрес статьи: https://arxiv.org/pdf/2410.21272.
В целом, это исследование представляет собой углубленный анализ «странных» стратегий LLM в математических рассуждениях, открывает нам новую перспективу для понимания ограничений LLM и указывает направление будущих исследований. Я считаю, что с постоянным развитием технологий математические возможности LLM будут значительно улучшены.