ในห้องปฏิบัติการนี้ เราจะนำสูตรทางคณิตศาสตร์ที่เราเห็นในบทที่แล้วมาปฏิบัติจริง เพื่อดูว่า MLE ทำงานอย่างไรกับการแจกแจงแบบปกติ
คุณจะสามารถ:
หมายเหตุ: *สามารถดูที่มาโดยละเอียดของสมการ MLE ทั้งหมดพร้อมการพิสูจน์ได้ที่เว็บไซต์นี้ -
เรามาดูตัวอย่างของ MLE และการกระจายที่เหมาะสมกับ Python ด้านล่าง ที่นี่ scipy.stats.norm.fit คำนวณพารามิเตอร์การกระจายโดยใช้การประมาณค่าความน่าจะเป็นสูงสุด
from scipy . stats import norm # for generating sample data and fitting distributions
import matplotlib . pyplot as plt
plt . style . use ( 'seaborn' )
import numpy as np sample = Nonestats.norm.fit(data) เพื่อให้พอดีกับการแจกแจงข้อมูลข้างต้น param = None
#param[0], param[1]
# (0.08241224761452863, 1.002987490235812)x = np.linspace(-5,5,100) x = np . linspace ( - 5 , 5 , 100 )
# Generate the pdf from fitted parameters (fitted distribution)
fitted_pdf = None
# Generate the pdf without fitting (normal distribution non fitted)
normal_pdf = None # Your code here 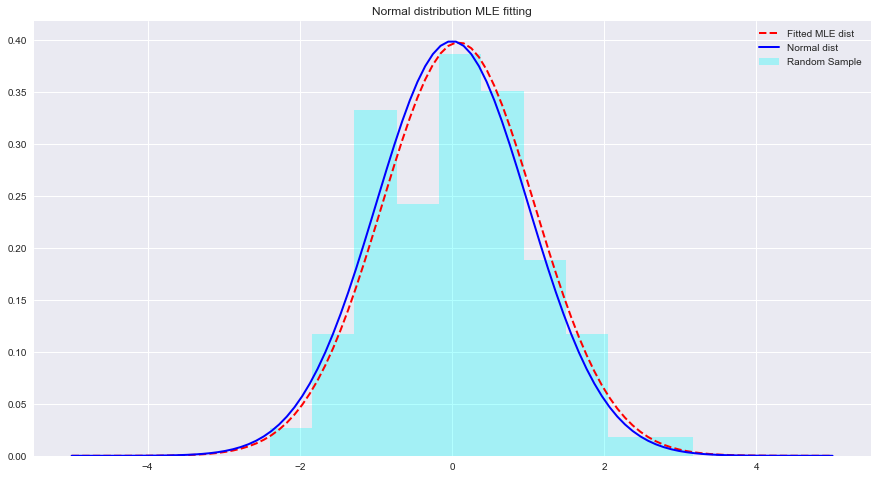
# Your comments/observations ในห้องทดลองสั้นๆ นี้ เราดูที่การตั้งค่าแบบเบย์ในบริบทแบบเกาส์เซียน เช่น เมื่อมีการแจกแจงตัวแปรสุ่มที่ซ่อนอยู่ตามปกติ เราได้เรียนรู้ว่า MLE สามารถประมาณค่าพารามิเตอร์ที่ไม่รู้จักของการแจกแจงแบบปกติได้ โดยการเพิ่มความน่าจะเป็นของค่าเฉลี่ยที่คาดไว้ให้สูงสุด ค่าเฉลี่ยคาดหวังจะเข้าใกล้ค่าเฉลี่ยของการแจกแจงแบบปกติที่ไม่พอดีภายในปริภูมิพารามิเตอร์นั้นมาก เราจะก้าวไปข้างหน้าด้วยความเข้าใจนี้ไปสู่การเรียนรู้ว่าการประมาณค่าดังกล่าวดำเนินการอย่างไรในการประมาณค่าเฉลี่ยของคลาสจำนวนหนึ่งที่มีอยู่ในการกระจายข้อมูลโดยใช้ Naive Bayes Classifier