เปลี่ยนเมทริกซ์โดยใช้เครือข่ายประสาท
เมทริกซ์แบบกลับด้านนำเสนอความท้าทายที่ไม่เหมือนใครสำหรับเครือข่ายประสาทส่วนใหญ่เนื่องจากข้อ จำกัด โดยธรรมชาติในการดำเนินการทางคณิตศาสตร์ที่แม่นยำเช่นการคูณและการแบ่งแยกในการเปิดใช้งาน เครือข่ายหนาแน่นแบบดั้งเดิมมักต้องการความช่วยเหลือเกี่ยวกับงานเหล่านี้เนื่องจากไม่ได้ออกแบบมาอย่างชัดเจนเพื่อจัดการกับความซับซ้อนที่เกี่ยวข้องกับการผกผันของเมทริกซ์ การทดลองที่ดำเนินการด้วยเครือข่ายประสาทที่มีความหนาแน่นอย่างง่ายได้แสดงให้เห็นถึงความยากลำบากอย่างมีนัยสำคัญในการเข้าร่วมการรุกรานเมทริกซ์ที่แม่นยำ แม้จะมีความพยายามต่าง ๆ ในการเพิ่มประสิทธิภาพสถาปัตยกรรมและกระบวนการฝึกอบรมผลลัพธ์มักจะต้องมีการปรับปรุง อย่างไรก็ตามการเปลี่ยนเป็นสถาปัตยกรรมที่ซับซ้อนมากขึ้น-เครือข่ายที่เหลือ 7 ชั้น (RESNET)-สามารถนำไปสู่การปรับปรุงประสิทธิภาพการทำงานที่ทำเครื่องหมายไว้
สถาปัตยกรรม Resnet ซึ่งเป็นที่รู้จักกันดีในการเรียนรู้การเป็นตัวแทนลึกผ่านการเชื่อมต่อที่เหลือได้พิสูจน์แล้วว่ามีประสิทธิภาพในการแก้ปัญหาการผกผันของเมทริกซ์ ด้วยพารามิเตอร์นับล้านเครือข่ายนี้สามารถจับรูปแบบที่ซับซ้อนภายในข้อมูลที่โมเดลที่ง่ายกว่าไม่สามารถทำได้ อย่างไรก็ตามความซับซ้อนนี้มีค่าใช้จ่าย: ข้อมูลการฝึกอบรมที่สำคัญเป็นสิ่งจำเป็นสำหรับการวางนัยทั่วไปที่มีประสิทธิภาพ
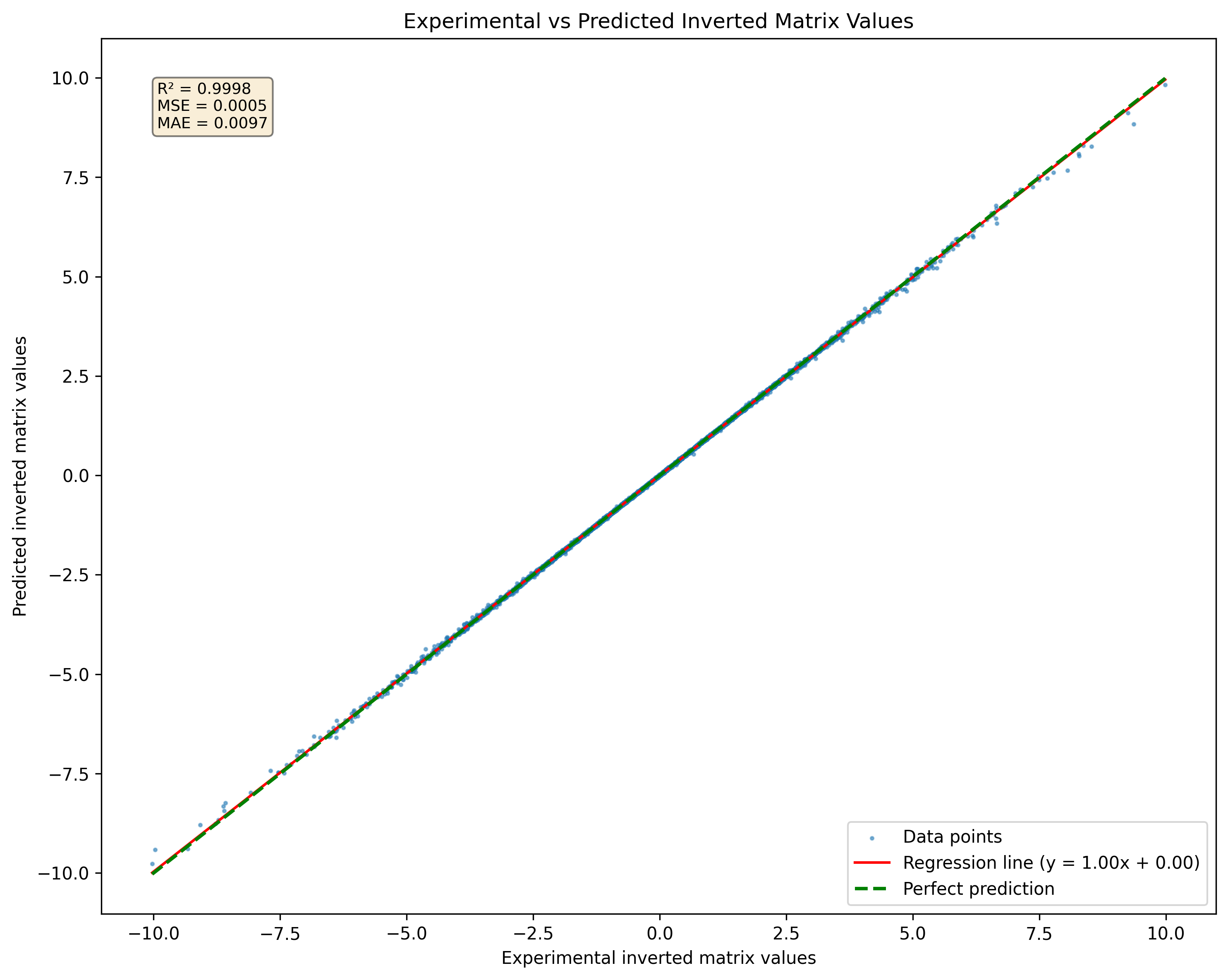รูปที่ 1: การสร้างภาพของเครือข่ายประสาทที่คาดการณ์ไว้
ในการประเมินประสิทธิภาพของเครือข่ายประสาทในการทำนายการรุกรานของเมทริกซ์ใช้ฟังก์ชั่นการสูญเสียที่เฉพาะเจาะจง:
ในสมการนี้:
เป้าหมายคือการลดความแตกต่างระหว่างเมทริกซ์ตัวตนและผลิตภัณฑ์ของเมทริกซ์ดั้งเดิมและผกผันที่คาดการณ์ไว้ ฟังก์ชั่นการสูญเสียนี้วัดได้อย่างมีประสิทธิภาพว่าการผกผันที่คาดการณ์ไว้นั้นใกล้เคียงกับความถูกต้อง
นอกจากนี้ถ้า
ฟังก์ชั่นการสูญเสียนี้มีข้อได้เปรียบที่แตกต่างกันมากกว่าฟังก์ชั่นการสูญเสียแบบดั้งเดิมเช่นค่าเฉลี่ยของข้อผิดพลาดกำลังสอง (MSE) หรือค่าเฉลี่ยข้อผิดพลาดสัมบูรณ์ (MAE)
การวัดโดยตรงของความแม่นยำในการผกผันเป้าหมายหลักของการผกผันของเมทริกซ์คือเพื่อให้แน่ใจว่าผลิตภัณฑ์ของเมทริกซ์และผกผันให้เมทริกซ์ตัวตน ฟังก์ชั่นการสูญเสียจับข้อกำหนดนี้โดยตรงโดยการวัดความเบี่ยงเบนจากเมทริกซ์ตัวตน ในทางตรงกันข้าม MSE และ MAE มุ่งเน้นไปที่ความแตกต่างระหว่างค่าที่คาดการณ์และค่าที่แท้จริงโดยไม่ต้องระบุคุณสมบัติพื้นฐานของเมทริกซ์ผกผันอย่างชัดเจน
เน้นความสมบูรณ์ของโครงสร้างโดยใช้ฟังก์ชั่นการสูญเสียที่ประเมินว่าผลิตภัณฑ์ AA - 1AA - 1 อยู่ใกล้แค่ไหนคือ II เน้นการรักษาความสมบูรณ์ของโครงสร้างของเมทริกซ์ที่เกี่ยวข้อง สิ่งนี้มีความสำคัญอย่างยิ่งในการใช้งานที่การรักษาความสัมพันธ์เชิงเส้นเป็นสิ่งสำคัญ ฟังก์ชั่นการสูญเสียแบบดั้งเดิมเช่น MSE และ MAE ไม่ได้คำนึงถึงแง่มุมของโครงสร้างนี้ซึ่งอาจนำไปสู่การแก้ปัญหาที่ลดข้อผิดพลาด แต่ล้มเหลวในการตอบสนองความต้องการทางคณิตศาสตร์ของการผกผันของเมทริกซ์
การบังคับใช้กับเมทริกซ์ที่ไม่ใช่ singular ฟังก์ชั่นการสูญเสียนี้โดยเนื้อแท้โดยเนื้อแท้ว่าเมทริกซ์ที่ถูกคว่ำเป็นแบบไม่ได้เป็น singular (เช่นกลับด้าน) ในสถานการณ์ที่มีเมทริกซ์เอกพจน์ฟังก์ชั่นการสูญเสียแบบดั้งเดิมอาจให้ผลลัพธ์ที่ทำให้เข้าใจผิดเนื่องจากพวกเขาไม่ได้อธิบายถึงความเป็นไปไม่ได้ที่จะได้รับการผกผันที่ถูกต้อง ฟังก์ชั่นการสูญเสียที่เสนอเน้นข้อ จำกัด นี้โดยการสร้างข้อผิดพลาดที่ใหญ่ขึ้นเมื่อพยายามกลับตัวเมทริกซ์เอกพจน์
ข้อ จำกัด ที่สำคัญอย่างหนึ่งเมื่อใช้เครือข่ายประสาทสำหรับการผกผันของเมทริกซ์คือการไม่สามารถจัดการเมทริกซ์เอกพจน์ได้อย่างมีประสิทธิภาพ เมทริกซ์เอกพจน์ไม่มีค่าผกผัน ดังนั้นความพยายามใด ๆ ของเครือข่ายประสาทเพื่อทำนายผกผันสำหรับเมทริกซ์ดังกล่าวจะให้ผลลัพธ์ที่ไม่ถูกต้อง ในทางปฏิบัติหากมีการนำเสนอเมทริกซ์เอกพจน์ในระหว่างการฝึกอบรมหรือการอนุมานเครือข่ายอาจยังคงผลลัพธ์ แต่ผลลัพธ์นี้จะไม่ถูกต้องหรือมีความหมาย ข้อ จำกัด นี้ตอกย้ำความสำคัญของการสร้างความมั่นใจว่าข้อมูลการฝึกอบรมประกอบด้วยเมทริกซ์ที่ไม่ใช่ singular เมื่อใดก็ตามที่เป็นไปได้
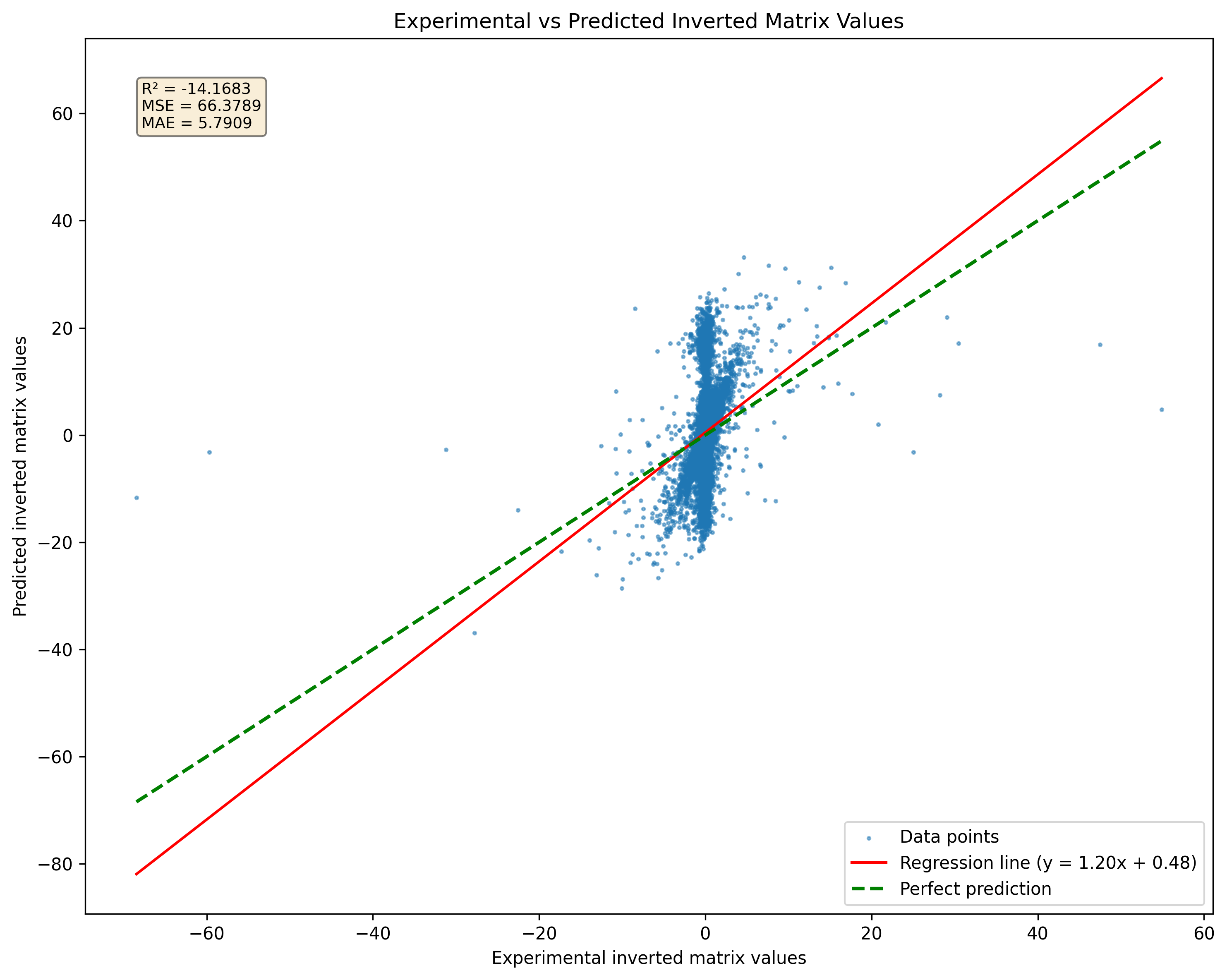รูปที่ 2: การเปรียบเทียบการทำนายแบบจำลองสำหรับเมทริกซ์เอกพจน์เมื่อเทียบกับ pseudoinversions โปรดทราบว่าแบบจำลองจะให้ผลลัพธ์โดยไม่คำนึงถึงความเป็นเอกเทศของเมทริกซ์
การวิจัยระบุว่าแบบจำลอง ResNet สามารถจดจำตัวอย่างที่ดีได้โดยไม่สูญเสียความแม่นยำอย่างมีนัยสำคัญ อย่างไรก็ตามการเพิ่มขนาดของชุดข้อมูลเป็น 10 ล้านตัวอย่างอาจนำไปสู่การ overfitting อย่างรุนแรง การ overfitting นี้เกิดขึ้นแม้จะมีข้อมูลจำนวนมาก แต่เน้นว่าการเพิ่มขนาดชุดข้อมูลไม่รับประกันการปรับปรุงทั่วไปสำหรับแบบจำลองที่ซับซ้อน เพื่อจัดการกับความท้าทายนี้กลยุทธ์การสร้างข้อมูลอย่างต่อเนื่องสามารถนำมาใช้ แทนที่จะพึ่งพาชุดข้อมูลแบบคงที่ตัวอย่างสามารถสร้างได้ทันทีและป้อนเข้าสู่เครือข่ายเมื่อสร้างขึ้น วิธีการนี้ซึ่งมีความสำคัญในการบรรเทาการ overfitting ไม่เพียง แต่ให้ตัวอย่างการฝึกอบรมที่หลากหลาย แต่ยังทำให้มั่นใจได้ว่าแบบจำลองนั้นได้สัมผัสกับชุดข้อมูลที่พัฒนาอย่างต่อเนื่อง
โดยสรุปในขณะที่การผกผันของเมทริกซ์เป็นสิ่งที่ท้าทายสำหรับเครือข่ายประสาทเนื่องจากข้อ จำกัด ในการดำเนินการทางคณิตศาสตร์การใช้ประโยชน์จากสถาปัตยกรรมขั้นสูงเช่น ResNet สามารถให้ผลลัพธ์ที่ดีขึ้น อย่างไรก็ตามต้องพิจารณาอย่างรอบคอบกับข้อกำหนดของข้อมูลและความเสี่ยงที่มากเกินไป การสร้างตัวอย่างการฝึกอบรมอย่างต่อเนื่องสามารถปรับปรุงกระบวนการเรียนรู้ของแบบจำลองและปรับปรุงประสิทธิภาพในงานเมทริกซ์ผกผัน เวอร์ชันนี้ยังคงรักษาเสียงที่ไม่มีตัวตนในขณะที่พูดคุยถึงความท้าทายและกลยุทธ์ในการฝึกอบรมเครือข่ายประสาทสำหรับการผกผันของเมทริกซ์
DeepMatrixInversion มีการแจกจ่ายภายใต้ใบอนุญาต LGPLV3
หากต้องการทราบรายละเอียดเพิ่มเติมว่าใบอนุญาตทำงานอย่างไรโปรดอ่านไฟล์ "ใบอนุญาต" หรือไปที่ "http://www.gnu.org/licenses/lgpl-3.0.html"
DeepMatrixInversion ปัจจุบันเป็นทรัพย์สินของ Giuseppe Marco Randazzo
ในการติดตั้งพื้นที่เก็บข้อมูล DeepMatrixInversion คุณสามารถเลือกระหว่างการใช้บทกวี, PIP หรือ PIPX ด้านล่างเป็นคำแนะนำสำหรับทั้งสองวิธี
git clone https://github.com/gmrandazzo/DeepMatrixInversion.git
cd DeepMatrixInversion
python3 -m venv .venv
. .venv/bin/activate
pip install poetry
poetry install
สิ่งนี้จะตั้งค่าสภาพแวดล้อมของคุณด้วยแพ็คเกจที่จำเป็นทั้งหมดเพื่อเรียกใช้ DeepMatrixInversion
สร้างสภาพแวดล้อมเสมือนจริงและติดตั้ง deppmatrixInversion ด้วย pip
python3 -m venv .venv
. .venv/bin/activate
pip install git+https://github.com/gmrandazzo/DeepMatrixInversion.git
หากคุณต้องการใช้ PIPX ซึ่งช่วยให้คุณติดตั้งแอปพลิเคชัน Python ในสภาพแวดล้อมที่แยกได้ให้ทำตามขั้นตอนเหล่านี้:
python3 -m pip install --user pipx
apt-get install pipx
brew install pipx
sudo dnf install pipx
pipx ติดตั้ง git+https: //github.com/gmrandazzo/deepmatrixinversion.git
ในการฝึกอบรมโมเดลที่สามารถทำการผกผันเมทริกซ์คุณจะใช้คำสั่ง dmxtrain คำสั่งนี้ช่วยให้คุณสามารถระบุพารามิเตอร์ต่าง ๆ ที่ควบคุมกระบวนการฝึกอบรมเช่นขนาดของเมทริกซ์ช่วงของค่าและระยะเวลาการฝึกอบรม
dmxtrain --msize < matrix_size > --rmin < min_value > --rmax < max_value > --epochs < number_of_epochs > --batch_size < size_of_batches > --n_repeats < number_of_repeats > --mout < output_model_path > dmxtrain --msize --rmin -1 --rmax 1 --epochs 5000 --batch_size 1024 --n_repeats 3 --mout ./Model_3x3
--msize <matrix_size>: Specifies the size of the square matrices to be generated for training. For example, 3 for 3x3 matrices.
--rmin <min_value>: Sets the minimum value for the random elements in the matrices. For instance, -1 will allow negative values.
--rmax <max_value>: Sets the maximum value for the random elements in the matrices. For example, 1 will limit values to a maximum of 1.
--epochs <number_of_epochs>: Defines how many epochs (complete passes through the training dataset) to run during training. A higher number typically leads to better performance; in this case, 5000.
--batch_size <size_of_batches>: Determines how many samples are processed before the model is updated. A batch size of 1024 means that 1024 samples are used in each iteration.
--n_repeats <number_of_repeats>: Indicates how many times to repeat the training process with different random seeds or initializations. This can help ensure robustness; for instance, repeating 3 times.
--mout <output_model_path>: Specifies where to save the trained model. In this example, it saves to ./Model_3x3.
เมื่อคุณฝึกอบรมโมเดลแล้วคุณสามารถใช้เพื่อทำการผกผันเมทริกซ์ในเมทริกซ์อินพุตใหม่ คำสั่งสำหรับการอนุมานคือ dmxinvert ซึ่งใช้เมทริกซ์อินพุตและส่งออกผกผัน
คำเตือน: DMXInvert สามารถกลับตัวเมทริกซ์ที่ใหญ่กว่าที่ใช้ในการฝึกอบรมโมเดลผ่านสูตรการผกผันของเชอร์แมน-มอร์ริสัน-วูดเบอรีบล็อก คุณลักษณะนี้ใช้งานได้เฉพาะกับเมทริกซ์ที่มีขนาดบล็อกสามารถหารด้วยขนาดบล็อกการฝึกอบรมแบบจำลองโดยไม่ต้องแจ้งเตือน คุณลักษณะนี้มีการทดลองอย่างมากและอาจต้องมีการแก้ไข
dmxinvert --inputmx <input_matrix_file> --inverseout <output_csv_file> --model <model_path>
dmxinvert --inputmx input_matrix.csv --inverseout output_inverse.csv --model ./Model_3x3_*
--inputmx <input_matrix_file>: Specifies the path to the input matrix file that you want to invert. This file should contain a valid matrix format (e.g., CSV).
--inverseout <output_csv_file>: Indicates where to save the resulting inverted matrix. The output will be saved in CSV format.
--model <model_path>: Provides the path to the trained model that will be used for performing the inversion.
การสร้างชุดข้อมูลเทียมด้วยอินพุตเมทริกซ์และเอาต์พุตกลับด้านทำ DMX DMXDatasetGenerator
dmxdatasetgenerator 3 10 -1 1 test_3x3_range_-1+1
สิ่งนี้จะสร้างเมทริกซ์ 10 ขนาด 3x3 ที่มีตัวเลขอยู่ในช่วงตั้งแต่ -1 ถึง +1
dmxdatasetgenerator [matrix size] [number of samples] [range min] [range max] [outname_prefix]
จากนั้นชุดข้อมูลสามารถตรวจสอบได้โดยใช้ dmxDataSetverify
dmxdatasetverify test_3x3_range_-1+1_matrices_3x3.mx test_3x3_range_-1+1_matrices_inverted_3x3.mx invertible
Dataset valid.
dmxdatasetverify [dataset matrix to invert] [dataset matrix inverted] [type: invertible or singular]
ไฟล์อินพุตเมทริกซ์ควรจัดรูปแบบดังนี้:
0.24077047370124594,-0.5012474139608847,-0.5409542929032876
-0.6257864520097793,-0.030705148203584942,-0.13723920334288975
-0.48095686716222064,0.19220406568380666,-0.34750000491973854
END
0.4575368007107925,0.9627977617090073,-0.4115240560547333
0.5191433428806012,0.9391491187187144,-0.000952683255491138
-0.17757763984424968,-0.7696584771443977,-0.9619759413623306
END
-0.49823271153034154,0.31993947803488587,0.9380291202366384
0.443652116558352,0.16745965310481048,-0.267270356721347
0.7075720067281346,-0.3310912886946993,-0.12013367141105102
END
แต่ละบล็อกของตัวเลขแสดงถึงเมทริกซ์แยกต่างหากตามด้วยเครื่องหมายสิ้นสุดที่ระบุจุดสิ้นสุดของเมทริกซ์นั้น
