
and the Fiber tasks in React, and different Fiber tasks have different priorities. React needs to process tasks with high priority first. For example, the user's clicks and inputs are high-priority tasks, because the user's operations definitely hope to have immediate effects, so as to improve the user experience. For example, the priority of animation events must be lower. After a new high-priority task enters the queue, React needs to process it first.
To store these tasks, there are two task pools in React.
// Tasks are stored on a min heap var taskQueue = []; var timerQueue = [];
taskQueue and timerQueue are both arrays. The former stores tasks to be executed immediately, while the latter stores tasks that can be delayed.
var newTask = {
id: taskIdCounter++, // Mark task id
callback, // callback function priorityLevel, // task priority startTime, // task start time, time point expirationTime, // expiration time, time point sortIndex: -1, // task sorting, the value comes from the expiration time, so the value The smaller the value, the higher the priority}; Once a new task comes in React, it will first use currentTime to record the current time (performance.now() or Date.now()). If the task has a delay parameter, then the task starts execution time. startTime = currentTime + delay;. Next, if startTime > currentTime is established, it proves that the task can be postponed, then the task enters the timerQueue, otherwise it enters the taskQueue.
How does React find the task with the highest priority? Take taskQueue as an example. It is a dynamic task pool (task queue), and the data form is an array. Of course, you can sort according to priority, that is, Array.sort. When a new task is added to the queue, it is sorted first, and then the task with the highest priority is found and executed. But the average time complexity of Array.sort is O(nlogn), which is not the best solution.
SortIndex is used for sorting in taskQueue's newTask. This value is taken from the expiration time, which means that the higher the priority task, the more it needs to be understood and executed, so the expiration time will be smaller. In other words, the higher the priority, the expiration time. The smaller the time, the smaller the sortIndex will naturally be. In fact, this is a priority queue .
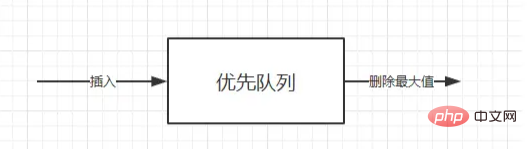
Priority queue is also a kind of queue ( first of all, it is a queue, and secondly, tail in, first out ). The only difference is that the dequeue order of the priority queue is based on priority; in some cases, you may need to find The minimum or maximum element in the element set can be operated by using the priority queue ADT. The priority queue ADT is a data structure that supports inserting and deleting minimum value operations (returning and deleting the minimum element) or deleting the maximum value operation (returning and deleting the minimum element). remove the largest element).
If the element with the smallest key value has the highest priority, then this priority queue is called an ascending priority queue (that is, the smallest element is always deleted first). Similarly, if the element with the largest key value has the highest priority, then this type of priority queue is called a descending priority queue (that is, the largest element is always deleted first); since these two types are symmetrical, you only need to focus on one of them. kind, such as ascending priority queue.
For example : when we were buying tickets, we were all queuing up and had the same priority. Whoever was in front of the queue would buy the ticket first. But then a soldier came and he had a higher priority and was directly in the queue. The front.
Minimum heap (small root heap, small top heap...) is used in React to achieve this function. That is to turn the taskQueue into a minimum heap, then take out the top task for execution, heap the taskQueue, and maintain it as a minimum heap data structure. When inserting a new task into the taskQueue, it must also be heaped and always keep it as a minimum heap.
: In some places, the heap is called a priority queue (not accurate). First of all, it is a queue and has the characteristics of a queue, that is, " first in, first out ". Secondly, the elements in this queue have priorities, and those with higher priorities will be ranked first.
To be precise, a heap is a way to implement a priority queue. Of course, priority queues can also be implemented in other ways.
We said before that heap sorting is an unstable sorting, but taskQueue hopes that this process is stable. That is to say, if it is possible that the expiration time of two tasks is the same, then it depends on who enters first. The task pool is the value of the id of newTask. Every time a new task comes, the id will be increased by 1.
function compare(a, b) {
// Compare sort index first, then task id.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
} Before understanding the minimum heap, let’s review the basic knowledge.
refers to an ordered tree in which the degree of the nodes in the tree is no greater than 2. It is the simplest and most important tree.
is a binary tree in which all nodes on each level have two child nodes, except for the last level which does not have any child nodes.
From a graphical perspective, a full binary tree looks like a triangle.
If the number of levels of a binary tree is K and the total number of nodes is (2^k) -1, then it is a full binary tree.
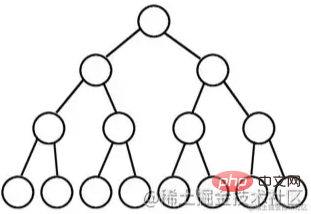
A full binary tree means "daughters have both sides" and is very perfect, so it is called a full binary tree.
excluding leaf nodes, the degree of all nodes is 2. In other words, the degree of all nodes can only be 0 or 2.
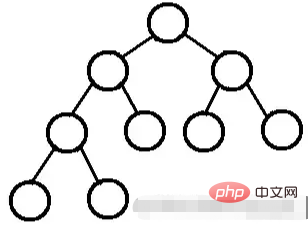
A perfect binary tree has either no children or both children.
The original English text of Full Binary Tree:
A Full Binary Tree (FBT) is a tree in which every node other than the leaves has two children.
The original English text of the perfect binary tree:
A Perfect Binary Tree (PBT) is a tree with all leaf nodes at the same depth. All internal nodes have degree 2.
All foreign books refer to the earliest translated textbooks on full binary trees and perfect binary trees, but the earliest translated articles are wrongly translated. Now in China, we can only make mistakes when they are wrong (everyone is wrong, then the wrong one is also right. For example, lobbyists...). If you want to discuss these two concepts with foreign friends, you should pay attention.
ABinary Tree (CBT) is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
A binary tree with n nodes of depth k , number the nodes in the tree from top to bottom and from left to right. If the node numbered i (1≤i≤n) is in the binary tree with the node numbered i in the full binary tree, If the positions are the same, the binary tree is called a complete binary tree.
The heap always satisfies the following properties:
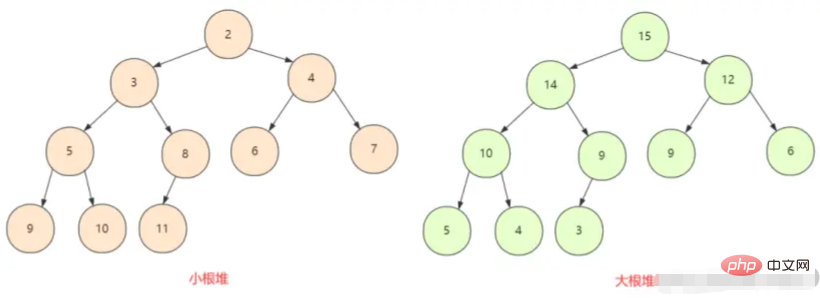
we must first understand the big root heap and the small root heap. In a complete binary tree All nodes are larger (or smaller) than their child nodes, so there are two situations here, the maximum heap and the minimum heap.
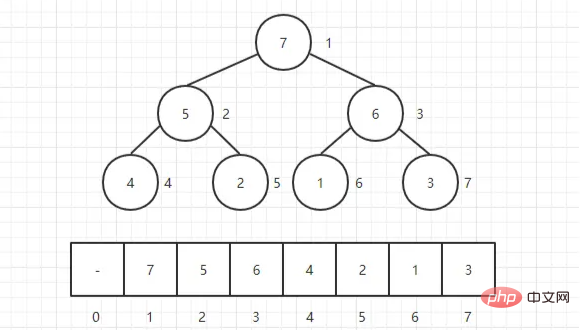
The heap is usually an array of objects that can be viewed as a complete binary tree . Of course, binary trees can also be represented by arrays.
is to build the heap first and then adjust it.
, for a binary tree (array representation), we adjust from bottom to top, starting from the "first non-leaf node" and adjusting forward. The rules for adjustment are as follows:
Building a heap is O(n) time complexity process.
① Start from the first non-leaf node to judge the swap down (shiftDown), so that the current node and child can maintain the heap properties
② However, ordinary node replacement may not be a problem. If the exchange breaks the heap structure properties of the child, then it must be re- ShiftDown the swapped node until stopped.
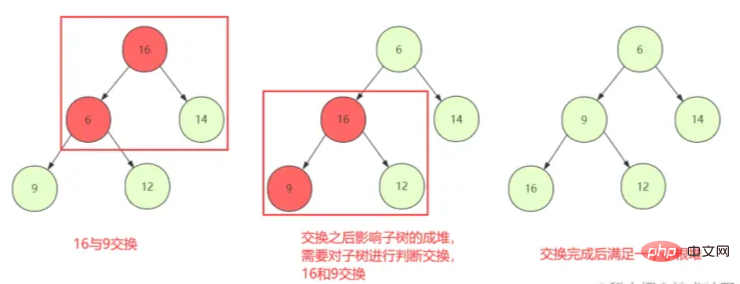
the heap
Destroy the heap structure.
① So simply put the last element first. In this way, you only need to judge the swap shift (shiftDown), but you need to note that the size of the entire heap has changed at this time. We will not logically use the discarded position, so we need to include a heap size parameter when designing the function. .
② Repeat the above operation until all elements in the heap are obtained.
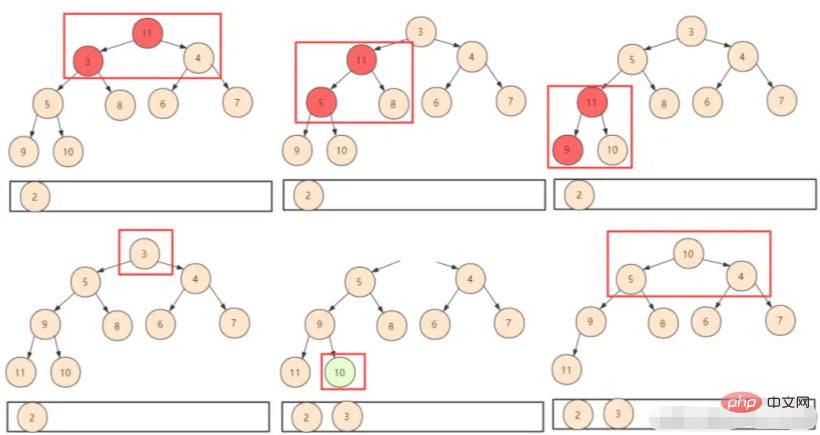
In terms of analysis of the complexity of the heap algorithm, the previous heap building time complexity was O(n). Each time the top of the heap is deleted and then swapped downwards, the number of each is logn. In this way, the complexity is O(nlogn), and the total time complexity is O(n)+O(nlogn)=O(nlogn).
Heap is suitable for maintaining the maximum value of the collection.
After an element is popped out of the heap, the cost of re-adjusting to obtain the top element of the heap (that is, the second highest value) is relatively low, because after the element is popped out, the heap is a semi-finished product, and the second highest value is obtained from a semi-finished product. Of course, the cost is relatively low, and the time complexity is O(logn), but if it is traversed once to find the second highest value, the time complexity is O(n).
code is written in Javascript ES6.
class Heap {
constructor(data, comp) {
this.data = data ? data : [];
// Comparison rules: more flexible, you can compare values or objects this.compartor = comp ? comp : (ab) => ab;
// Adjust to heap (priority queue)
this.heapify();
}
heapify() {
if(this.size() <= 1) return;
// Start adjusting from the first non-leaf node, or you can adjust from the last element for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//Adjust the heap. Downward adjustment can also be implemented using recursion. Here, iteration is used to implement this.shiftDown(i);
}
}
// Adjust downward shiftDown(i) {
let left = 2*i +1;
let right = 2*i +2;
let len = this.size();
while(i < len) {
let findIndex = i;
//The left child is "bigger"
if(left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
findIndex = left;
}
// The right child is "bigger"
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = right;
}
if(i !== findIndex) {
//Exchange the current node with a larger value [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// After adjusting this layer, it may affect the characteristics of the lower layer's heap, so continue to adjust the lower layer (iterative implementation, or recursive)
i = findIndex;
left = 2*i +1;
right = 2*i +2;
}
else {
// If no adjustment is needed, jump out (must jump out, otherwise the loop cannot end)
break;
}
}
}
// Adjust upward shiftUp(i){
// Find the subscript of parent let parentIndex = Math.floor((i-1)/2);
// Adjust the maximum to 0
while(parentIndex >=0 ) {
let findIndex = i;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = parentIndex;
}
if(findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = findIndex;
parentIndex = Math.floor((i-1)/2);
}
else {
break;
}
}
}
// Get the number of all elements in the heap size(){
return this.data.length;
}
// Get the first element of the heap peek(){
if(!this.size()) return null;
return this.data[0];
}
//Add an element to the heap push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// Pop the first element from the heap pop(){
if(!this.size()) return null;
let res = this.data[0];
if(this.size() == 1) {
this.data.pop();
}
else {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
this.shiftDown(0);
}
return res;
}
} let arr = [2,9,8,6,3,10,5,7,4,1];
let comp = (a, b) => ab;
let heap = new Heap(arr, comp);
let res = [];
while(heap.size()) {
res.push(heap.pop());
}
console.log(res); The element in arr can also be an object.
The directory packages/scheduler in the React source code is the code related to React's task scheduling module.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* Copyright (c) Facebook, Inc. and its affiliates.
*
* This source code is licensed under the MIT license found in the
* LICENSE file in the root directory of this source tree.
*
* @flow strict
*/
type Heap = Array<Node>;
type Node = {|
ID: number,
sortIndex: number,
|};
export function push(heap: Heap, node: Node): void {
const index = heap.length;
heap.push(node);
siftUp(heap, node, index);
}
export function peek(heap: Heap): Node | null {
const first = heap[0];
return first === undefined ? null : first;
}
export function pop(heap: Heap): Node | null {
const first = heap[0];
if (first !== undefined) {
const last = heap.pop();
if (last !== first) {
heap[0] = last;
siftDown(heap, last, 0);
}
return first;
} else {
return null;
}
}
function siftUp(heap, node, i) {
let index = i;
while (true) {
const parentIndex = (index - 1) >>> 1;
const parent = heap[parentIndex];
if (parent !== undefined && compare(parent, node) > 0) {
// The parent is larger. Swap positions.
heap[parentIndex] = node;
heap[index] = parent;
index = parentIndex;
} else {
// The parent is smaller. Exit.
return;
}
}
}
function siftDown(heap, node, i) {
let index = i;
const length = heap.length;
while (index < length) {
const leftIndex = (index + 1) * 2 - 1;
const left = heap[leftIndex];
const rightIndex = leftIndex + 1;
const right = heap[rightIndex];
// If the left or right node is smaller, swap with the smaller of those.
if (left !== undefined && compare(left, node) < 0) {
if (right !== undefined && compare(right, left) < 0) {
heap[index] = right;
heap[rightIndex] = node;
index = rightIndex;
} else {
heap[index] = left;
heap[leftIndex] = node;
index = leftIndex;
}
} else if (right !== undefined && compare(right, node) < 0) {
heap[index] = right;
heap[rightIndex] = node;
index = rightIndex;
} else {
// Neither child is smaller. Exit.
return;
}
}
}
function compare(a, b) {
// Compare sort index first, then task id.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
} The minimum heap we implemented is slightly different from the implementation in React, but the idea is the same, only the code is written differently.
task scheduling in React is implemented using the minimum heap. If we have a certain understanding of the minimum heap before, we will learn this content faster. Personally, I think how important it is to accumulate knowledge in the early stage, but this process may be boring. At this time, do you think you know some algorithms? In fact, these algorithms are entry-level, and you have not even started yet. Because in React's task scheduling scenario, the requirements to be implemented are very clear, and the data structures and algorithms to be used are also clear. In some actual scenarios, we know the specific requirements, but we don’t know what data results and algorithms to use. We need to abstract the requirements and design specific data structures and algorithms based on the abstract data model. These are the key points. .