dsa.js data structures algorithms javascript下載 - dsa.js data structures algorithms javascript原始碼下載

dsa.js data structures algorithms javascript

其他源碼

2.7.6

下載

JavaScript 中的資料結構與演算法

這是 DSA.js 書的編碼實作和 NPM 套件的儲存庫。

在此儲存庫中，您可以找到 JavaScript 中演算法和資料結構的實作。該材料可以用作開發人員的參考手冊，也可以在面試前刷新特定主題。此外，您還可以找到更有效解決問題的想法。

互動式資料結構

安裝

您可以複製儲存庫或從 NPM 安裝程式碼：

npm install dsa.js

然後你可以將它匯入到你的程式或 CLI 中

 const { LinkedList , Queue , Stack } = require ( 'dsa.js' ) ;

有關所有可用資料結構和演算法的列表，請參閱index.js。

特徵

演算法是每個程式設計師必不可少的工具箱。

當您必須對資料進行排序、在大數據集中搜尋值、轉換資料、將程式碼擴展到許多用戶等時，您將需要注意演算法在運行時。演算法只是解決問題所遵循的步驟，而資料結構是儲存資料以供以後操作的地方。兩者結合起來創建程式。

演算法+資料結構=程式。

大多數程式語言和函式庫確實提供了基本資料結構和演算法的實作。然而，為了正確使用資料結構，您必須了解權衡以選擇最適合工作的工具。

本資料將教您：

？應用策略來解決演算法問題。永遠不會再陷入困境。在面試中取得好成績！
✂️ 建構高效的演算法。了解如何將問題分解為可管理的部分。
？透過了解基本的電腦科學概念，提高您解決問題的能力並成為一名全面的開發人員。
？涵蓋基本主題，例如大 O 時間、資料結構和必須了解的演算法。從頭開始實作 10 多個資料結構。

裡面有什麼

所有程式碼和解釋都可以在此存儲庫中找到。您可以從（src 資料夾）中挖掘連結和程式碼範例。不過，內聯程式碼範例並未展開（因為 Github 的 asciidoc 限制），但您可以按照路徑查看實作。

注意：如果您喜歡更線性地使用訊息，那麼書籍格式會更適合您。

這些主題分為四個主要類別，如下所示：

？演算法分析

計算機科學的金塊沒有任何繁瑣的內容。 （點擊展開）
計算機科學的金塊，沒有所有的繁文縟節
了解從程式碼範例計算運行時間
了解如何使用 Big O 表示法比較演算法。 （點擊展開）
了解如何使用 Big O 表示法比較演算法。
使用 Big O 表示法比較演算法
假設您想尋找數組中的重複項。使用大 O 表示法，我們可以比較解決相同問題的不同解決方案，但在完成所需時間方面存在巨大差異。
使用地圖的最佳解決方案
尋找數組中的重複項（簡單方法）
8個例子用程式碼解釋如何計算時間複雜度。 （點擊展開）
8個例子用程式碼解釋如何計算時間複雜度
最常見的時間複雜度
時間複雜度圖

？線性資料結構

了解最常見資料結構的來龍去脈。 （點擊展開）
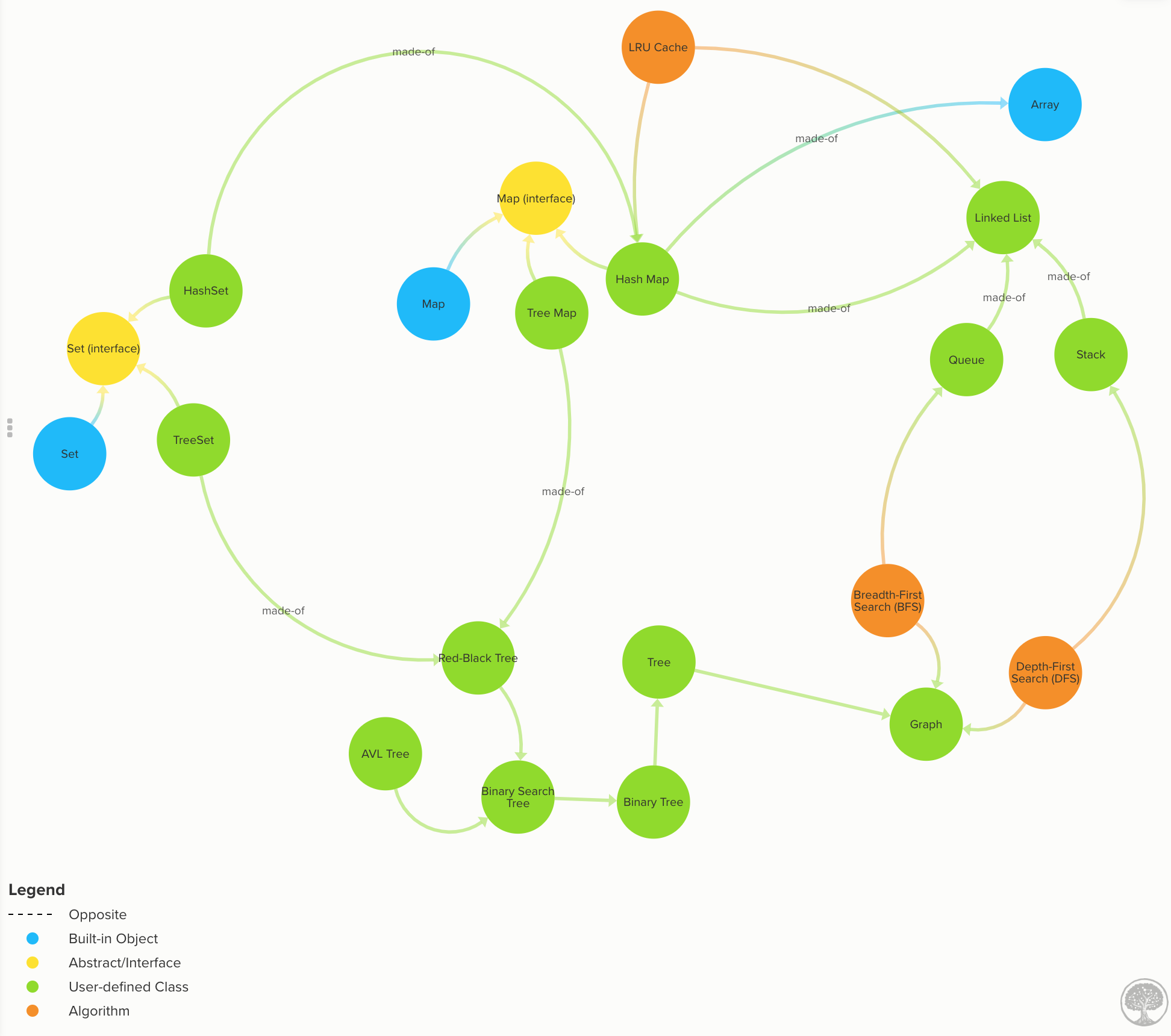
了解最常見資料結構的來龍去脈
數組：在大多數語言中內置，因此此處未實現。數組時間複雜度
鍊錶：每個資料節點都有一個到下一個（和上一個）的連結。代碼|鍊錶時間複雜度
佇列：資料以「先進先出」（FIFO）方式流動。代碼|隊列時間複雜度
堆疊：資料以「後進先出」（LIFO）方式流動。代碼|堆疊時間複雜度
何時使用陣列或鍊錶。了解權衡。 （點擊展開）
何時使用陣列或鍊錶。了解權衡
當…時使用數組
您需要以隨機順序快速存取資料（使用索引）。
您的資料是多維的（例如矩陣、張量）。
在以下情況下使用連結列表：
您將按順序存取您的資料。
您想要節省記憶體並僅在需要時分配記憶體。
您需要恆定的時間從清單的極端中刪除/新增。
當尺寸要求未知時 - 動態尺寸優勢
建構列表、堆疊和佇列。 （點擊展開）
從頭開始建立清單、堆疊和佇列
從頭開始建立以下任何資料結構：
鍊錶
堆疊
佇列

？非線性資料結構

了解最通用的資料結構之一：哈希圖。 （點擊展開）
哈希映射
了解如何實現不同類型的地圖，例如：
哈希映射
樹狀圖
另外，了解不同 Maps 實作之間的差異：
HashMap更省時。 TreeMap更節省空間。
TreeMap搜尋複雜度為O(log n) ，而優化的HashMap平均為O(1) 。
HashMap的鍵按插入順序排列（或隨機，取決於實作）。 TreeMap的鍵總是排序的。
TreeMap免費提供一些統計數據，例如：取得最小值、取得最大值、中位數、查找鍵範圍。 HashMap沒有。
TreeMap保證始終為O(log n) ，而HashMap的攤餘時間為O(1) ，但在極少數情況下重新散列，則需要O(n) 。
了解圖和樹的性質。 （點擊展開）
了解圖和樹的屬性
圖表
透過大量圖像和插圖了解所有圖形屬性。
圖：可以與零個或多個相鄰節點有連接或邊的資料節點。與樹不同，節點可以有多個父節點、循環。代碼|圖時間複雜度
樹木
了解所有不同種類的樹木及其特性。
樹：資料節點有零個或多個相鄰節點（也稱為子節點）。每個節點只能有一個父節點，否則是圖，而不是樹。代碼|文件
二元樹：與樹相同，但最多只能有兩個孩子。代碼|文件
二元搜尋樹（BST）：與二元樹相同，但節點值保持此順序left < parent < right 。代碼| BST 時間複雜度
AVL 樹：自平衡 BST 以最大化查找時間。代碼| AVL 樹文檔 |自平衡和樹旋轉文檔
紅黑樹：自平衡 BST 比 AVL 更寬鬆，以最大限度地提高插入速度。程式碼
實作二元搜尋樹以進行快速查找。
實現二元搜尋樹以進行快速查找
了解如何在樹中新增/刪除/更新值：
如何讓樹保持平衡？
從不平衡 BST 到平衡 BST
 1                           2
                         /   
   2        =>           1     3
    
     3

⚒ 演算法工具箱

透過 7 個簡單步驟解決問題，永遠不會陷入困境。 （點擊展開）
透過 8 個簡單步驟解決問題，永遠不會陷入困境
了解問題所在
建立一個簡單的範例（尚無邊緣情況）
集思廣益解決方案（貪心演算法、分而治之、回溯、暴力破解）
用簡單的例子測試你的答案（心理上）
最佳化解決方案
寫程式碼。是的，現在您可以編碼了。
測試你寫的程式碼
分析空間和時間的複雜性，並確保進一步優化。
完整詳細資訊請參閱此處
掌握最受歡迎的排序演算法（歸併排序、快速排序等） （點擊展開）
掌握最受歡迎的排序演算法
我們將探索三種基本的 O(n^2) 排序演算法，它們具有較低的開銷：
冒泡排序。代碼|文件
插入排序。代碼|文件
選擇排序。代碼|文件
然後討論有效的排序演算法 O(n log n) 例如：
歸併排序。代碼|文件
快速排序。代碼|文件
學習解決問題的不同方法，例如分而治之、動態規劃、貪心演算法和回溯。 （點擊展開）
學習解決演算法問題的不同方法
我們將討論以下解決演算法問題的技術：
貪婪演算法：使用啟發式做出貪婪選擇，以找到最佳解決方案而不回頭。
動態規劃：當存在許多重疊子問題時加速遞歸演算法的技術。它使用記憶來避免重複工作。
分而治之：將問題分成更小的部分，解決每個子問題，然後連結結果。
回溯：搜尋所有（或部分）可能的路徑。但是，它會停止，並在發現當前解決方案不起作用後立即返回。
蠻力：產生所有可能的解決方案並嘗試所有解決方案。（將其用作最後的手段或作為起點）。