In den letzten Jahren haben große Sprachmodelle (LLMs) in verschiedenen Bereichen erstaunliche Fähigkeiten gezeigt, ihre mathematischen Denkfähigkeiten sind jedoch überraschend schwach. Der Herausgeber von Downcodes interpretiert für Sie eine aktuelle Studie, die das unglaubliche „Geheimnis“ von LLM in arithmetischen Operationen enthüllt, und analysiert die Grenzen dieser Methode und die Richtung zukünftiger Verbesserungen. Diese Forschung vertieft nicht nur unser Verständnis des internen Funktionsmechanismus von LLM, sondern liefert auch eine wertvolle Referenz für die Verbesserung der mathematischen Fähigkeiten von LLM.
In letzter Zeit haben KI-Modelle für große Sprachen (LLM) bei verschiedenen Aufgaben gute Arbeit geleistet, darunter beim Schreiben von Gedichten, beim Schreiben von Code und beim Chatten. Aber können Sie es glauben? Beim Lösen einfacher Rechenaufgaben kommt es häufig zu Überschlägen, was überraschend ist.
Eine aktuelle Studie hat das „seltsame“ Geheimnis hinter den arithmetischen Denkfähigkeiten von LLM gelüftet: Sie verlassen sich weder auf leistungsstarke Algorithmen noch auf das Gedächtnis, sondern verfolgen eine Strategie namens „heuristisches Sammelsurium“. Das ist wie bei einem Studenten, der sich nicht ernsthaft mit mathematischen Formeln und Theoremen beschäftigt. verlässt sich aber auf etwas „ein wenig Klugheit“ und „Faustregeln“, um die Antwort zu erhalten.
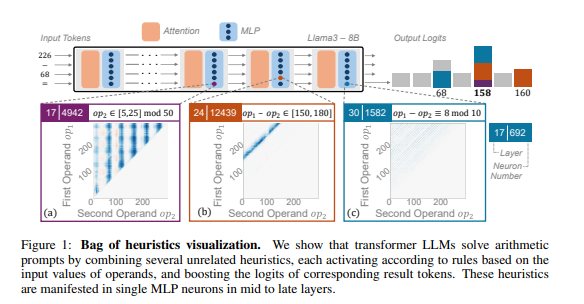
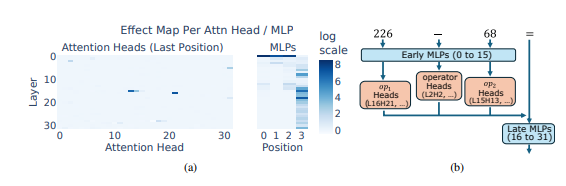
Die Forscher verwendeten arithmetisches Denken als typische Aufgabe und führten eine eingehende Analyse mehrerer LLMs wie Llama3, Pythia und GPT-J durch. Sie fanden heraus, dass der Teil des LLM-Modells, der für arithmetische Berechnungen verantwortlich ist (der sogenannte „Schaltkreis“), aus vielen einzelnen Neuronen besteht, von denen jedes wie ein „Miniaturrechner“ fungiert und nur für die Erkennung spezifischer numerischer Muster und die entsprechende Ausgabe verantwortlich ist Antwort. Beispielsweise könnte ein Neuron dafür verantwortlich sein, „Zahlen zu identifizieren, deren einzelne Ziffer 8 ist“, während ein anderes Neuron dafür verantwortlich sein könnte, „Subtraktionsoperationen zu identifizieren, deren Ergebnisse zwischen 150 und 180 liegen“.
Diese „Mini-Rechner“ sind wie ein Durcheinander von Werkzeugen, und anstatt sie nach einem bestimmten Algorithmus zu verwenden, verwendet LLM eine zufällige Kombination dieser „Werkzeuge“, um eine Antwort basierend auf dem eingegebenen Zahlenmuster zu berechnen. Es ist wie bei einem Koch, der kein festes Rezept hat, sondern es nach Belieben anhand der verfügbaren Zutaten mischt und am Ende eine „dunkle Küche“ kreiert.
Noch überraschender ist, dass diese „heuristische Sammelsurium“-Strategie tatsächlich in den frühen Stadien der LLM-Ausbildung auftauchte und im Verlauf der Ausbildung schrittweise verbessert wurde. Das bedeutet, dass LLM von Anfang an auf diesen „Patchwork“-Ansatz beim Denken setzt, anstatt diese Strategie erst zu einem späteren Zeitpunkt zu entwickeln.
Welche Probleme wird diese „seltsame“ arithmetische Argumentationsmethode also verursachen? Forscher haben herausgefunden, dass die „heuristische Sammelsurium“-Strategie nur eine begrenzte Verallgemeinerungsfähigkeit aufweist und fehleranfällig ist. Dies liegt daran, dass LLM über eine begrenzte Anzahl „kleiner Klugheiten“ verfügt und diese „kleinen Klugheiten“ selbst auch Fehler aufweisen können, die sie daran hindern, beim Auftreffen auf neue numerische Muster korrekte Antworten zu geben. Genau wie ein Koch, der nur „Tomaten-Rührei“ zubereiten kann, wird er, wenn er plötzlich gebeten wird, „geschnetzeltes Schweinefleisch mit Fischgeschmack“ zuzubereiten, es definitiv eilig haben und ratlos sein.
Diese Studie zeigte die Grenzen der arithmetischen Denkfähigkeit des LLM auf und zeigte auch die Richtung auf, in der die mathematischen Fähigkeiten des LLM in der Zukunft verbessert werden können. Forscher glauben, dass es möglicherweise nicht ausreicht, sich ausschließlich auf vorhandene Trainingsmethoden und Modellarchitekturen zu verlassen, um die arithmetischen Denkfähigkeiten von LLM zu verbessern. Es müssen neue Methoden erforscht werden, um LLM dabei zu helfen, leistungsfähigere und allgemeinere Algorithmen zu erlernen, damit sie wirklich „mathematische Meister“ werden können.
Papieradresse: https://arxiv.org/pdf/2410.21272
Alles in allem bietet diese Studie eine eingehende Analyse der „seltsamen“ Strategien des LLM im mathematischen Denken, bietet uns eine neue Perspektive zum Verständnis der Grenzen des LLM und zeigt die Richtung für zukünftige Forschung auf. Ich glaube, dass mit der kontinuierlichen Weiterentwicklung der Technologie die mathematischen Fähigkeiten von LLM erheblich verbessert werden.