ในช่วงไม่กี่ปีที่ผ่านมา โมเดลภาษาขนาดใหญ่ (LLM) ได้แสดงให้เห็นถึงความสามารถที่น่าทึ่งในสาขาต่างๆ แต่ความสามารถในการให้เหตุผลทางคณิตศาสตร์ของพวกเขายังอ่อนแออย่างน่าประหลาดใจ บรรณาธิการของ Downcodes จะตีความการศึกษาล่าสุดสำหรับคุณ ซึ่งเผยให้เห็น "ความลับ" ที่น่าทึ่งของ LLM ในการดำเนินการทางคณิตศาสตร์ และวิเคราะห์ข้อจำกัดของวิธีการนี้และทิศทางของการปรับปรุงในอนาคต การวิจัยนี้ไม่เพียงแต่ช่วยเพิ่มความเข้าใจของเราเกี่ยวกับกลไกการทำงานภายในของ LLM ให้ลึกซึ้งยิ่งขึ้นเท่านั้น แต่ยังเป็นข้อมูลอ้างอิงที่มีคุณค่าสำหรับการปรับปรุงความสามารถทางคณิตศาสตร์ของ LLM
เมื่อเร็ว ๆ นี้ AI large language model (LLM) ทำงานได้ดีในด้านต่าง ๆ รวมถึงการเขียนบทกวี การเขียนโค้ด และการสนทนา พวกมันมีพลังอำนาจทุกอย่าง! แต่คุณเชื่อไหมว่า AI ที่มี "อัจฉริยะ" เหล่านี้เป็น "มือใหม่ทางคณิตศาสตร์" มักจะพลิกกลับเมื่อแก้ปัญหาเลขคณิตอย่างง่ายซึ่งน่าประหลาดใจ
การศึกษาล่าสุดได้เปิดเผยความลับที่ "แปลก" เบื้องหลังความสามารถในการให้เหตุผลทางคณิตศาสตร์ของ LLM: พวกเขาไม่ได้พึ่งพาอัลกอริธึมหรือหน่วยความจำอันทรงพลัง แต่ใช้กลยุทธ์ที่เรียกว่า "การผสมฮิวริสติก"! แต่อาศัย "ความฉลาดเล็กน้อย" และ "กฎทั่วไป" บางประการในการหาคำตอบ
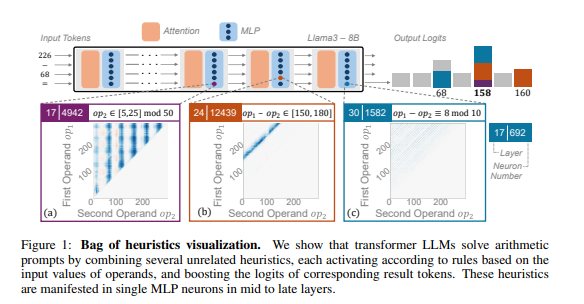
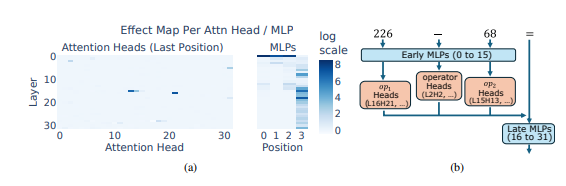
นักวิจัยใช้เหตุผลทางคณิตศาสตร์เป็นงานทั่วไป และดำเนินการวิเคราะห์เชิงลึกของ LLM หลายรายการ เช่น Llama3, Pythia และ GPT-J พวกเขาพบว่าส่วนหนึ่งของโมเดล LLM ที่รับผิดชอบในการคำนวณทางคณิตศาสตร์ (เรียกว่า "วงจร") ประกอบด้วยเซลล์ประสาทหลายตัว ซึ่งแต่ละเซลล์ทำหน้าที่เหมือน "เครื่องคิดเลขจิ๋ว" และมีหน้าที่เฉพาะในการรับรู้รูปแบบตัวเลขเฉพาะและส่งออกค่าที่สอดคล้องกันเท่านั้น คำตอบ. ตัวอย่างเช่น เซลล์ประสาทหนึ่งอาจมีหน้าที่ในการระบุ "ตัวเลขที่มีหลักเดียวคือ 8" ในขณะที่อีกเซลล์ประสาทหนึ่งอาจมีหน้าที่ในการระบุ "การดำเนินการลบซึ่งผลลัพธ์อยู่ระหว่าง 150 ถึง 180"
"เครื่องคิดเลขขนาดเล็ก" เหล่านี้เป็นเหมือนเครื่องมือที่สับสนวุ่นวาย และแทนที่จะใช้ตามอัลกอริธึมเฉพาะ LLM ใช้ "เครื่องมือ" เหล่านี้รวมกันแบบสุ่มเพื่อคำนวณคำตอบตามรูปแบบของตัวเลขที่ป้อน มันเหมือนกับพ่อครัวที่ไม่มีสูตรตายตัว แต่ผสมตามใจชอบตามส่วนผสมที่มีอยู่ และสุดท้ายก็ทำ "อาหารสีเข้ม"
สิ่งที่น่าประหลาดใจยิ่งกว่านั้นก็คือ กลยุทธ์ "การผสมผสานฮิวริสติก" นี้เกิดขึ้นจริงในช่วงแรกของการฝึกอบรม LLM และค่อยๆ ปรับปรุงเมื่อการฝึกอบรมดำเนินไป ซึ่งหมายความว่า LLM อาศัยแนวทาง "การปะติดปะต่อ" นี้ในการให้เหตุผลตั้งแต่เริ่มแรก แทนที่จะพัฒนากลยุทธ์นี้ในภายหลัง
ดังนั้นวิธีการให้เหตุผลทางคณิตศาสตร์ที่ "แปลก" นี้จะทำให้เกิดปัญหาอะไรขึ้น นักวิจัยพบว่ากลยุทธ์ "การประสมกันแบบฮิวริสติก" มีความสามารถในการสรุปทั่วไปที่จำกัดและมีแนวโน้มที่จะเกิดข้อผิดพลาด เนื่องจาก LLM มี "ความฉลาดเล็กๆ น้อยๆ" ในจำนวนจำกัด และ "ความฉลาดเล็กๆ น้อยๆ" เหล่านี้เองก็อาจมีข้อบกพร่องที่ทำให้ไม่สามารถให้คำตอบที่ถูกต้องเมื่อเผชิญกับรูปแบบตัวเลขใหม่ๆ เช่นเดียวกับเชฟที่ทำได้แค่ "ไข่คนมะเขือเทศ" เท่านั้น หากจู่ๆ เขาก็ขอให้ทำ "หมูฝอยรสปลา" เขาก็จะต้องรีบและขาดทุนแน่นอน
การศึกษาครั้งนี้เผยให้เห็นข้อจำกัดของความสามารถในการให้เหตุผลทางคณิตศาสตร์ของ LLM และยังชี้ให้เห็นทิศทางในการปรับปรุงความสามารถทางคณิตศาสตร์ของ LLM ในอนาคต นักวิจัยเชื่อว่าการพึ่งพาวิธีการฝึกอบรมที่มีอยู่และสถาปัตยกรรมแบบจำลองเพียงอย่างเดียวอาจไม่เพียงพอที่จะปรับปรุงความสามารถในการให้เหตุผลทางคณิตศาสตร์ของ LLM และจำเป็นต้องสำรวจวิธีการใหม่ๆ เพื่อช่วยให้ LLM เรียนรู้อัลกอริธึมทั่วไปที่มีประสิทธิภาพมากขึ้น เพื่อให้สามารถเป็น "ผู้เชี่ยวชาญทางคณิตศาสตร์" ได้อย่างแท้จริง
ที่อยู่กระดาษ: https://arxiv.org/pdf/2410.21272
โดยรวมแล้ว การศึกษานี้ให้การวิเคราะห์เชิงลึกเกี่ยวกับกลยุทธ์ "แปลก" ของ LLM ในการให้เหตุผลทางคณิตศาสตร์ ให้มุมมองใหม่ให้เราเข้าใจข้อจำกัดของ LLM และชี้ให้เห็นทิศทางสำหรับการวิจัยในอนาคต ฉันเชื่อว่าด้วยเทคโนโลยีการพัฒนาอย่างต่อเนื่อง ความสามารถทางคณิตศาสตร์ของ LLM จะดีขึ้นอย่างมาก