แบบจำลองภาษาขนาดใหญ่ (LLM) แสดงความสามารถที่น่าทึ่งในหลาย ๆ สาขา研究人员深入分析了 llama3、 Pythia 和 gpt-j 等多个 llm, 发现它们并非依靠强大的算法或记忆力进行计算, 而是采用一种“ 启发式大杂烩” 的策略, 如同一个靠“ 小聪明” 和“ กฎของคำตอบ "คำตอบของมองโกเลีย
เมื่อเร็ว ๆ นี้รูปแบบภาษา AI ขนาดใหญ่ (LLM) ทำงานได้ดีในงานต่าง ๆ พวกเขามักจะพลิกกลับเมื่อต้องรับมือกับคำถามเลขคณิตง่าย ๆ ซึ่งน่าแปลกใจ
การศึกษาล่าสุดเผยให้เห็นความลับ "วิเศษ" ที่อยู่เบื้องหลังความสามารถในการใช้เหตุผลทางคณิตศาสตร์ LLM: พวกเขาไม่ได้พึ่งพาอัลกอริทึมที่แข็งแกร่งหรือพึ่งพาความทรงจำ แต่ใช้กลยุทธ์ที่เรียกว่า "แรงบันดาลใจของ Hodgepodge"! ทฤษฎีบทอย่างระมัดระวัง แต่พึ่งพา "ความฉลาดน้อย" และ "กฎกฏหมาย" เพื่อตอบ
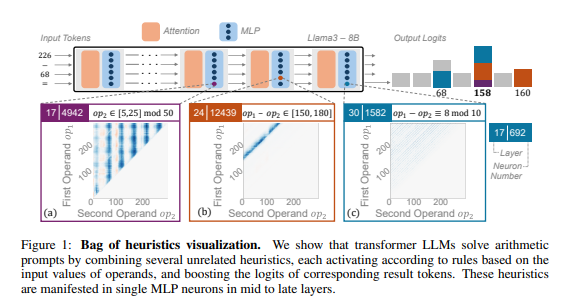
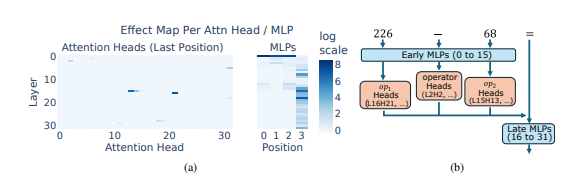
นักวิจัยใช้การใช้เหตุผลทางคณิตศาสตร์เป็นงานทั่วไปในการวิเคราะห์เชิงลึกของ LLM หลายตัวเช่น Llama3, Pythia และ GPT-J พวกเขาพบว่าแบบจำลอง LLM มีหน้าที่ในการคำนวณทางคณิตศาสตร์ (เรียกว่า "วงจร") ซึ่งประกอบด้วยเซลล์ประสาทเดี่ยวจำนวนมาก โหมดดิจิตอลและส่งออกคำตอบการติดต่อที่สอดคล้องกัน ตัวอย่างเช่นเซลล์ประสาทอาจรับผิดชอบในการระบุ "ตัวเลขที่มี 8 หลัก" และเซลล์ประสาทอื่นมีหน้าที่ในการระบุ "การลบการดำเนินการระหว่าง 150 ถึง 180"
"เครื่องคิดเลขขนาดเล็ก" เหล่านี้เป็นเหมือนเครื่องมือที่ยุ่งเหยิง นี่เป็นเหมือนพ่อครัวไม่มีสูตรคงที่ แต่ในส่วนผสมที่มีอยู่ในมือและในที่สุดก็ทำ "อาหารมืด"
สิ่งที่น่าประหลาดใจยิ่งกว่านั้นคือกลยุทธ์ "แรงบันดาลใจฮอดจ์พ็อดจ์" นี้ปรากฏขึ้นจริงในช่วงต้นของการฝึกอบรม LLM และค่อยๆดีขึ้นด้วยการฝึกอบรม ซึ่งหมายความว่า LLM อาศัย "ชิ้นส่วนชิ้นนี้" ตั้งแต่ต้นแทนที่จะพัฒนากลยุทธ์นี้ในช่วงต่อมา
ดังนั้นวิธีการให้เหตุผลทางคณิตศาสตร์ "วิเศษ" นี้คืออะไร นี่เป็นเพราะจำนวน "ความฉลาดขนาดเล็ก" ที่จัดขึ้นโดย LLM นั้นมี จำกัด และ "ความฉลาดน้อย" เหล่านี้อาจมีข้อบกพร่องในตัวเองทำให้พวกเขาไม่สามารถให้คำตอบที่ถูกต้องเมื่อพวกเขาพบโมเดลดิจิตอลใหม่ เช่นเดียวกับพ่อครัวที่ทำแค่ "ไข่กวนมะเขือเทศ" เขาก็ทำให้เขาทำ "ปลาหั่นฝอยหั่นฝอย"
การศึกษาครั้งนี้เปิดเผยถึงข้อ จำกัด ของความสามารถในการใช้เหตุผลทางคณิตศาสตร์ LLM และยังชี้ให้เห็นถึงทิศทางสำหรับการปรับปรุงความสามารถทางคณิตศาสตร์ของ LLM ในอนาคต นักวิจัยเชื่อว่าการใช้วิธีการฝึกอบรมที่มีอยู่และสถาปัตยกรรมแบบจำลองอาจไม่เพียงพอที่จะปรับปรุงความสามารถในการใช้เหตุผลทางคณิตศาสตร์ของ LLM
ที่อยู่วิทยานิพนธ์: https://arxiv.org/pdf/2410.21272
การวิจัยนี้ไม่เพียง แต่อธิบายถึงการขาด LLM ในการคำนวณทางคณิตศาสตร์ แต่ยังมีที่สำคัญกว่านั้นคือทิศทางการอ้างอิงที่มีค่าสำหรับการปรับปรุงในอนาคตของ LLM ในการวิจัยในอนาคตเราต้องให้ความสนใจกับวิธีการปรับปรุงความสามารถในการเรียนรู้ทั่วไปและอัลกอริทึมการเรียนรู้ของ LLM เพื่อแก้ปัญหาข้อบกพร่องในการใช้เหตุผลทางคณิตศาสตร์และทำให้ความสามารถทางคณิตศาสตร์ที่ทรงพลังอย่างแท้จริง