俄罗斯版本的任务可以在存储库中找到。

加载级别2…
加载大厅…
您最近去过类似的大厅。还是很久以前?很难说。一切都混淆了。再次,您可以从大厅的远处听到声音。这意味着您并不孤单。今天,大厅照亮了,井井有条。品种很好。
突然,您会听到扬声器的清晰,完美的声音:
你好。
让我自我介绍。我是沉思和分析模块M-53。由于未知的原因,我发现自己在这个相当无聊的大厅里。这是一个很大的责任和东西,但是这里没有什么可考虑的。
当我开发时,我还从某些有趣的文章中学到了其他材料。它的纸质副本在框A1B18中。是的,就在这里。我对您的要求很小:从文章中发展生活游戏;希望这会让我有些愉快。和平。图形可能非常简单:我很开放。终端中的伪图会很好。如果可以使用矩阵和思考初始化状态,那就太好了。最好将至少5个原始初始化与经典集合(稳定的人物,甲壳虫,周期性人物,移动人物,枪支,puffer火车,食客,反射器,育种者等)进行准备也是一个好主意。
我期待看到您的想法!
谢谢。
==任务收到。在C中开发一个SRC/GAME_OF_LIFE.C程序 - 生命游戏的可视化。要显示图形,仅使用ASCII字符(输出到终端)。您需要实施生活游戏的交互式版本。还可以创建调整“游戏”速度的选项。 ==
将运动场视为“游戏”状态的矩阵。假定该场“封闭于自身”,例如,在右下方,右侧的邻居是左下方的正方形,底部的邻居是右上方。通过Stdin提供“游戏”状态的原始初始化。通过输入重定向准备至少5个具有初始状态的文件,以快速启动和初始化。
游戏必须以C为C,具有结构化的样式,并从终端延伸;
您的源代码将由静态分析仪cppcheck以及样式的linter cpplint测试。
有关如何在计算机上运行这些测试的说明在materials文件夹中。
请勿使用笨重的功能,请限制多达40行(不包括main )。
检查您的程序是否有内存泄漏!
开发游戏时,请遵循E. Dijkstra结构化编程的原则。
加载中...
生命的游戏,也简单地被称为生活,是由英国数学家约翰·霍顿·康威(John Horton Conway)在1970年设计的蜂窝自动机。它是一款零游戏游戏,这意味着它的演变是由其初始状态决定的,不需要进一步的投入。一个人通过创建初始配置并观察其发展方式来与生活游戏互动。它已经完成,可以模拟通用构造函数或任何其他图灵机。
生命游戏的宇宙是方形细胞的无限,二维正交网格,每个网格在两个可能的状态之一中,是生命或死亡的一种状态之一(或人口稠密的人群)。每个细胞都与其八个邻居相互作用,这些邻居是水平,垂直或对角线相邻的细胞。在每个时间步骤中,都会发生以下过渡:
任何少于两个现场邻居的活细胞死亡,就好像人口不足一样。任何具有两个或三个现场邻居的活细胞都将生活在下一代。任何具有三个以上邻居的活细胞死亡,就好像被人口过多一样。任何具有三个活的邻居的死细胞都会成为一个活细胞,就好像通过繁殖一样。这些规则将自动机的行为与现实生活进行比较,可以凝结为以下内容:
任何具有两个或三个活的邻居的活细胞都能幸存。任何拥有三个活邻居的死细胞都会成为现场牢房。所有其他活细胞都死于下一代。同样,所有其他死细胞都死了。初始图案构成了系统的种子。第一代是通过同时应用于种子中每个单元格的上述规则来创建的。出生和死亡同时发生,而发生这种情况的离散时刻有时被称为tick虫。每一代都是前一个的纯函数。该规则继续反复应用以创建更多的世代。
1940年底,约翰·冯·诺伊曼(John von Neumann)将生命定义为一种创造(是存在或有机体),可以自身复制并模拟图灵机。冯·诺伊曼(Von Neumann)正在考虑一种工程解决方案,该解决方案将使用在液体或气体中随机漂浮的电磁成分。事实证明,当时可用的技术并不现实。 Stanislaw Ulam发明了细胞自动机,旨在模拟Von Neumann的理论电磁构建体。乌拉姆(Ulam)使用计算机在几篇论文中使用计算机在二维晶格中模拟其细胞自动机。同时,冯·诺伊曼(Von Neumann)试图构建ULAM的细胞自动机。尽管成功,但他忙于其他项目,并留下了一些未完成的细节。他的结构很复杂,因为它试图模拟他自己的工程设计。随着时间的流逝,其他研究人员提供了更简单的生活结构,并在论文和书籍中发表。
约翰·康威(John Conway)从数学逻辑中的问题和部分乌拉姆(Ulam)进行的模拟游戏中的一部分,约翰·康威(John Conway)从1968年开始进行实验,并使用各种不同的二维蜂窝自动机规则。自动机。例如,他希望一些配置能够持续很长时间,然后再垂死,而其他配置将永远继续下去,而无需允许周期。这是一个重大的挑战和一个开放的问题,直到蜂窝自动机的专家设法证明,实际上,生活的生命游戏已经承认了一种配置,而这种配置就满足了冯·诺伊曼(Von Neumann)的两个一般要求。尽管生活游戏前的定义是验证的,但康威的构造目的是简单,而没有先验的证明自动机已经活着。
康威经过大量实验,仔细选择了他的规则以满足这些条件:
不应该有爆炸性的增长。应该存在小的初始模式,并具有混乱,不可预测的结果。冯·诺伊曼通用构建体应该有潜力。在遵守上述约束的同时,规则应尽可能简单。该游戏在1970年10月的《科学美国人》(Scientific American)上首次公开露面,这是马丁·加德纳(Martin Gardner)的“数学游戏”专栏。从理论上讲,生活游戏具有通用图灵机的力量:可以在生命游戏中计算的任何可以计算算法的东西。加德纳(Gardner)写道:“由于人生的类比与生物社会的兴起,跌倒和改变,它属于所谓的“模拟游戏”(类似于现实生活中的游戏)的成长类别。”
自出版以来,人生游戏引起了人们的极大兴趣,因为模式可以发展出令人惊讶的方式。它提供了出现和自组织的例子。各个领域的学者,例如计算机科学,物理学,生物学,生物化学,经济学,数学,哲学和生成科学,都利用了从游戏简单规则实施的复杂模式可以浮出水面的方式。该游戏还可以用作教学类比,用于传达某种违反直觉的观念,即在没有设计师的情况下设计和组织可以自发出现。例如,认知科学家丹尼尔·丹尼特(Daniel Dennett宇宙。
人生游戏的普及得到了与越来越便宜的计算机访问同时进入的帮助。游戏可能会在这些机器上运行数小时,否则这些机器在晚上仍未使用。在这方面,它预示了后来的计算机生成的分形的普及。对于许多人来说,生活游戏只是一个编程挑战:使用其他浪费的CPU周期的有趣方式。但是,对于某些人来说,生活游戏具有更多的哲学含义。它在1970年代及以后发展了一个邪教。目前的发展甚至是在生命委员会游戏范围内创建计算机系统的理论仿真。
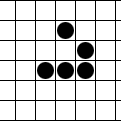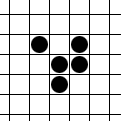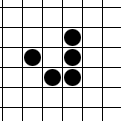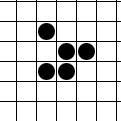
加载中...